Свойство периодичности

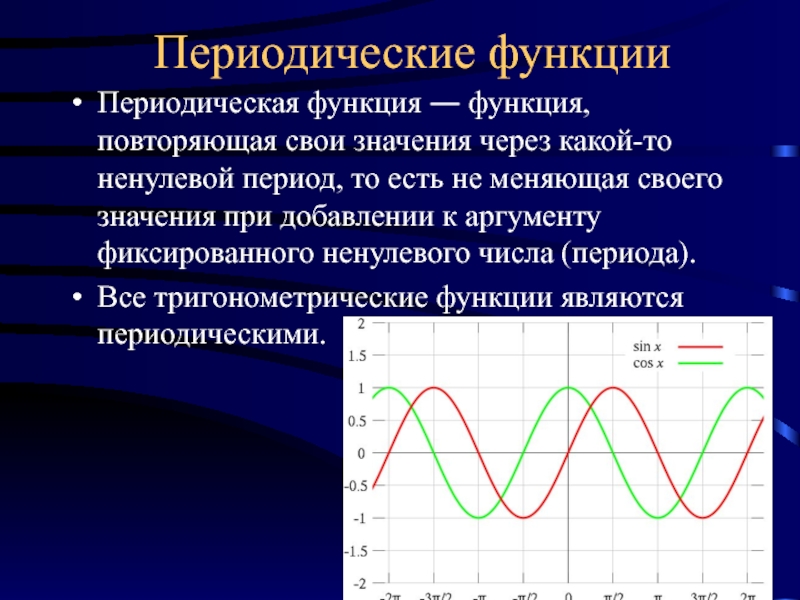
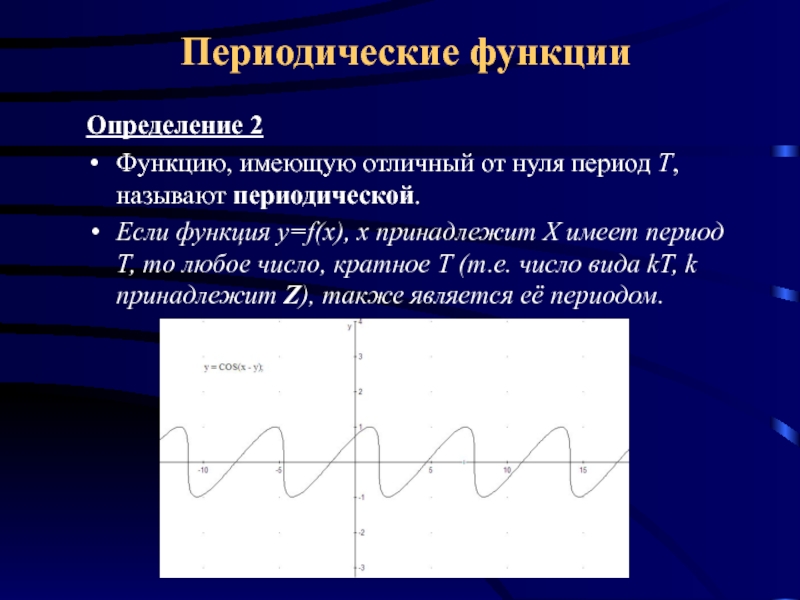
истечении некоторого промежутка времени.
Например, при вращении Земли вокруг Солнца

её расстояние от солнца всё время меняется, но после полного оборота Земля оказывается на том же расстоянии от солнца, сто и год тому назад. Возвращается на своё место после полного оборота и лопасть турбины.

Такие периодические повторяющиеся процессы описываются периодическими функциями.

ненулевой период, то есть не меняющая своего значения при добавлении

к аргументу фиксированного ненулевого числа (периода).
Все тригонометрические функции являются периодическими.

период Т, если для любого x принадлежит Х выполняются равенства

f(x-T)=f(x)=f(x+T).
Из этого определения следует, что если функция с периодом Т определена в точке х, то она определена в точках х+Т ,х-Т.
Любая функция имеет период, равный нулю(при Т=0 равенство превращается в тождество
f(x-0)=f(x)=f(x+0)).

функция y=f(x), x принадлежит Х имеет период Т, то любое

число, кратное Т (т.е. число вида kT, k принадлежит Z), также является её периодом.

Периодические функции

случаев среди положительных периодов периодической функции есть наименьший . Его

называют основным периодом этой функции, все остальные её периоды кратны основному периоду.

Если Т - основной период функции y=f(x), то для построения

её графика достаточно построить ветвь графика на одном из промежутков длины Т, а затем выполнить параллельный перенос этой ветви вдоль оси х на +Т,+2Т,+3Т, … .
Чаще всего в качестве такого промежутка длины Т выбирают промежуток с концами в точках (-Т/2;0)и(Т/2;0).

есть основной период. Классический пример - функция Дирихле y=d (x),

где

1,если х- рациональное число;
d (x)= 0,если х- иррациональное число.

самом деле, если х-рациональное число,
то х-r, x+r

–рациональные числа, а потому
d (x-r)=d (x)=d (x+r)=1.
Если же х – иррациональное число, то
х-r, х+r – иррациональные числа, а потому
d (x-r)=d (x)=d (x+r) = 0.

среди положительных рациональных чисел нет наименьшнго числа, значит,
у периодической

функции Дирихле нет основного периода.