Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проценты в прошлом и настоящем
Содержание
- 1. Проценты в прошлом и настоящем
- 2. Цель проектаЦель проекта - история появления процентов,
- 3. АктуальностьПроект предполагает сбор и анализ данных, их
- 4. Задачи проектаНаучиться решать основные задачи на проценты;Привить
- 5. ГипотезаМоя гипотеза – это формирование знаний и умений по применению процентов в жизненных ситуациях.
- 6. Происхождения термина процентСлово «процент» происходит от латинского
- 7. Или же так? Существует и другая версия
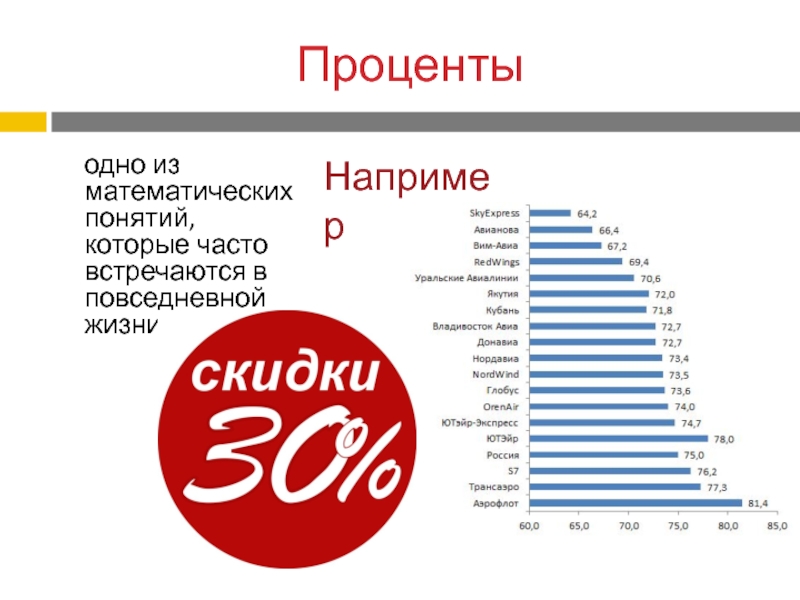
- 8. Проценты одно из математических понятий, которые часто встречаются в повседневной жизни.Например
- 9. РостовщичествоУже в далекой древности было распространено ростовщичество
- 10. Банковские операцииТех, кто берет в долг деньги
- 11. Вычисление процентов в банкеГде p% - годовая
- 12. Смеси, растворы, сплавыЗадачи на смеси, растворы и
- 13. Вычисление процентов в бытуОсновные понятия, связанные с
- 14. Задачи из прошлогоЗадача 1В романе М.Е. Салтыкова-Щедрина
- 15. Решение (1)Ответ: 4800 рублей Если вести расчет
- 16. Решение (2)Если вести расчет по сложным процентам,
- 17. Задача №2В Новелле О.Бальзака «Гобсек» один из
- 18. РешениеПо формуле сложных процентов: Sn=S∙(1 +
- 19. Задачи настоящегоБанк «Винни Пух и Пятачок» начисляет
- 20. Решение10% = 0,11+ 1∙0,1 = 1+0,1 =
- 21. Задача №2Агрофирма предполагает продать моркови на 10%
- 22. РешениеПусть q0 – объем продаж прошлого года
- 23. Задача №3Сколько граммов 30 %-го раствора надо
- 24. РешениеОтвет: 64 г
- 25. Задача С5Оля хочет взять кредит 1200000 рублей.
- 26. РешениеЕсли S – сумма кредита, годовые составляют
- 27. 1.200.000*1,1-320.000 = 1.000.000Проводим операцию аналогично, пока оставшаяся доля станет равна 0Ответ: 5 лет
- 28. С531 декабря 2014 года Арсений взял в
- 29. РешениеПусть сумма кредита равна S, годовые составляют
- 30. Решение
- 31. КризисВ 2015 году ставка по вкладам в
- 32. РешениеРассчитаем конечную сумму вклада по истечению срока
- 33. ПрименениеКак известно из практики с помощью процентов
- 34. ЗаключениеСейчас мы находимся в возрасте, когда нужно
- 35. Спасибо за внимание!
- 36. Скачать презентанцию
Цель проектаЦель проекта - история появления процентов, примеры повседневного использования процентных вычислений в прошлом и настоящем.
Слайды и текст этой презентации
Слайд 1ПРОЦЕНТЫ В ПРОШЛОМ И НАСТОЯЩЕМ
2015г.
Проект на тему:
Государственное бюджетное образовательное
учреждение средняя образовательная школа №222
Слайд 2Цель проекта
Цель проекта - история появления процентов, примеры повседневного использования
процентных вычислений в прошлом и настоящем.
Слайд 3Актуальность
Проект предполагает сбор и анализ данных, их представление в четком
визуальном виде. Он направлен на формирование понимания содержательного смысла термина
«процент», на формирование понимания оборотов речи с этим термином.Данный проект актуален так как применение процентных вычислений требуются не только на уроках математики, но и в быту
Слайд 4Задачи проекта
Научиться решать основные задачи на проценты;
Привить учащимся основы экономической
грамотности;
Сформировать умения производить процентные вычисления, необходимые для применения в практической
деятельности;Познакомиться с некоторыми банковскими операциями, при выполнении которых требуется применить проценты.
Слайд 5Гипотеза
Моя гипотеза – это формирование знаний и умений по применению
процентов в жизненных ситуациях.
Слайд 6Происхождения термина процент
Слово «процент» происходит от латинского слова pro centum,
что буквально переводится «за сотню», или «со ста»
Знак % происходит,
как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буквы t в наклонную черту произошел современный символ для обозначения процента.
Слайд 7Или же так?
Существует и другая версия возникновения этого знака. Предполагается,
что этот знак произошел в результате нелепой опечатки, совершенной наборщиком.
В 1685 году в Париже была опубликована книга – руководство по коммерческой арифметике, где по ошибке наборщик вместо cto напечатал %.
Слайд 8Проценты
одно из математических понятий, которые часто встречаются в повседневной
жизни.
Например
Слайд 9Ростовщичество
Уже в далекой древности было распространено ростовщичество – выдача денег
под проценты; разность называлась лихвой
1000 + (1000/100%*20%)=1200
В Древнем Вавилоне, например,
лихва составляла 20% и более. Это значит, что ремесленник, взявший 1000 у.е. сроком на год возвращал ему по прошествии года не менее 1200 у.е
Слайд 10Банковские операции
Тех, кто берет в долг деньги в банке под
проценты, называют заемщиками, а ссуду(величину взятую у банка) – кредитом.
Одним
из самых распространенных способов привлечения в банк сбережений граждан, фирм и т.д. является открытие вкладчиком сберегательного счета. При всех этих действиях вкладчик получает от банка плату в виде процентов за использование его денег для выдачи кредитов предпринимателям и т.д.
Слайд 11Вычисление процентов в банке
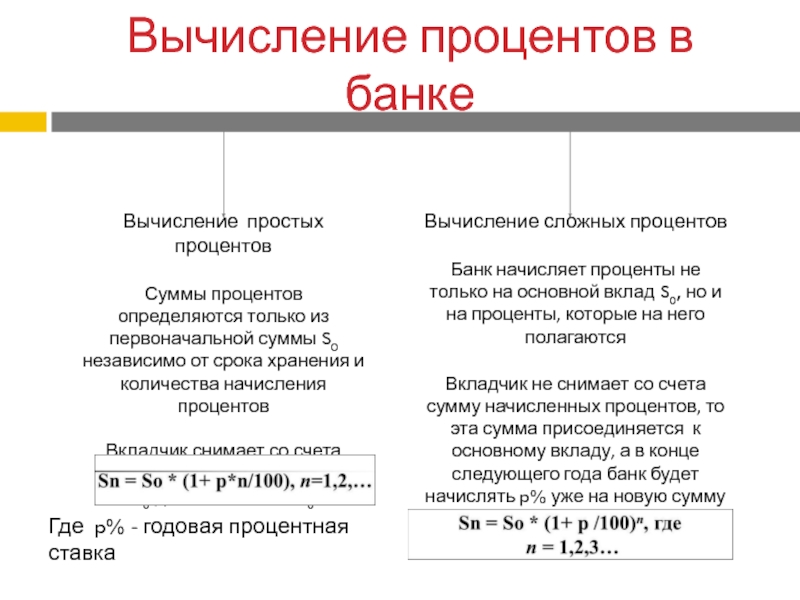
Где p% - годовая процентная ставка
Вычисление простых
процентов
Суммы процентов определяются только из первоначальной суммы S0 независимо от
срока хранения и количества начисления процентов Вкладчик снимает со счета зачисленные проценты, S0∙p/100, оставляя S0
Вычисление сложных процентов
Банк начисляет проценты не только на основной вклад S0, но и на проценты, которые на него полагаются
Вкладчик не снимает со счета сумму начисленных процентов, то эта сумма присоединяется к основному вкладу, а в конце следующего года банк будет начислять p% уже на новую сумму
Слайд 12Смеси, растворы, сплавы
Задачи на смеси, растворы и сплавы называют еще
задачами на процентное содержание или концентрации
Где w – процентная доля
mр.в.-
масса вещества в растворе/смеси/сплавеmр-ра – масса всего раствора/смеси/сплава
См Смесь состоит из «чистого вещества» и «примесей». Долей а чистого вещества в смеси называется отношение чистого количества вещества m в смеси к общему количеству M
Слайд 13Вычисление процентов в быту
Основные понятия, связанные с процентами:
Нахождение процентов данного
числа
Чтобы найти a% от b, надо
b∙0,01aНахождение числа по его процентам
Если известно, что a% числа x равно b, то x=b∕0,01a
Нахождение процентного отношения чисел
Чтобы найти процентное отношение числе, надо отношение этих чисел умножить на 100%
Слайд 14Задачи из прошлого
Задача 1
В романе М.Е. Салтыкова-Щедрина «Господа Головлевы» сын
Порфирия Владимировича Петя проиграл в карты казенные 3000 рублей и
попросил у бабушки деньги взаймы. Он говорил: «Я бы хороший процент дал. Пять процентов в месяц» Подсчитайте, сколько денег готов вернуть Петя через год, согласись бабушка на его условия.
Слайд 15Решение (1)
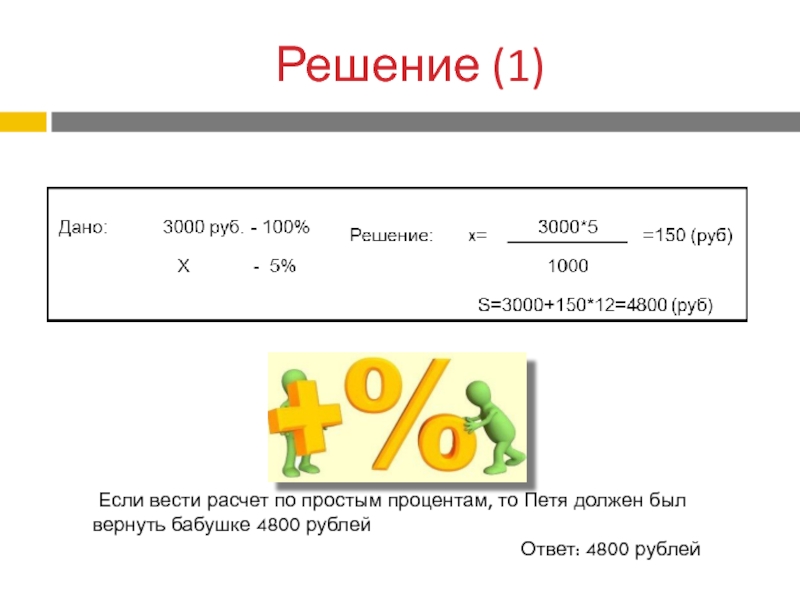
Ответ: 4800 рублей
Если вести расчет по простым процентам,
то Петя должен был вернуть бабушке 4800 рублей
Слайд 16Решение (2)
Если вести расчет по сложным процентам, то Петя должен
был вернуть бабушке 5400 рублей
Ответ:5400 рублей
Слайд 17Задача №2
В Новелле О.Бальзака «Гобсек» один из героев, господин Дервиль,
взял у ростовщика Гобсеку сумму в 150000 франков сроком на
10 лет под 15% годовых. Вычислите, какую сумму вернул Дервиль Гобсеку по прошествии всего срока.
Слайд 18Решение
По формуле сложных процентов:
Sn=S∙(1 + р/100)ⁿ, где n = 1,2,3,…
мы имеем
Sn= 150000·(1 + +0,15)10 = 150000· 4,0456 =
=
606 883,6 (франка)Ответ:606 883,6 франка
Слайд 19Задачи настоящего
Банк «Винни Пух и Пятачок» начисляет своим вкладчикам по
10$ ежемесячно. Иа сделал вклад в этот банк в размере
1,00$. Сколько денег он может снять со своего счета через два месяца?Задача №1
Слайд 20Решение
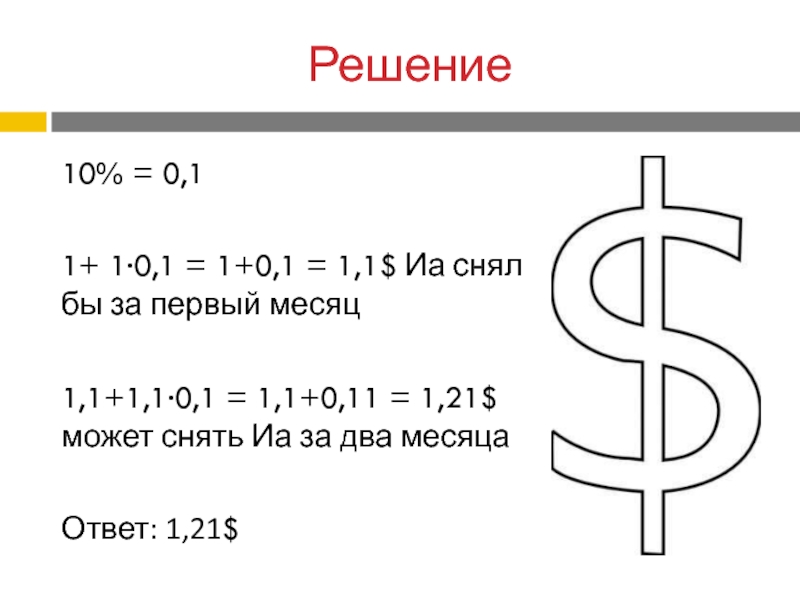
10% = 0,1
1+ 1∙0,1 = 1+0,1 = 1,1$ Иа снял
бы за первый месяц
1,1+1,1∙0,1 = 1,1+0,11 = 1,21$ может снять
Иа за два месяцаОтвет: 1,21$
Слайд 21Задача №2
Агрофирма предполагает продать моркови на 10% меньше, чем в
прошлом году. На сколько процентов агрофирма должна повысить цену на
свою морковь, чтобы получить за нее на 3,5% больше денег, чем в прошлом году.
Слайд 22Решение
Пусть q0 – объем продаж прошлого года
p0 – цена продаж прошлого года
p0q0 – выручка прошлого года q1 – объем продаж текущего года
p1 – цена продаж текущего года
p1q1 – выручка текущего года
x – доля повышения цена на морковь
По условию задачи p1q1 = 1,035 p0q0
причем q1 = 0,9q0
p1 = (1+x)∙p0
Слайд 23Задача №3
Сколько граммов 30 %-го раствора надо добавить к 80
г 12 %-го раствора этой же соли, чтобы получить 20
%-й раствор соли?
Слайд 25Задача С5
Оля хочет взять кредит 1200000 рублей. Погашение кредита происходит
раз в год равными суммами (кроме,может быть,последней) после начисления процентов.
Ставка процента 10% годовых.На какое минимальное количество лет может Оля взять кредит,что бы ежегодные выплаты были не более 320000 рублей?
Слайд 26Решение
Если S – сумма кредита, годовые составляют a%, то в
последний день каждого года оставшаяся сумма должна увеличиваться на коэффициент
m=1+0,01a
В
нашем случае m будет равно 1,1S, т.к. ставка равна 10%.Для того, чтобы проще решить задачу, составим таблицу.
Слайд 271.200.000*1,1-320.000 = 1.000.000
Проводим операцию аналогично, пока оставшаяся доля станет равна
0
Ответ: 5 лет
Слайд 28С5
31 декабря 2014 года Арсений взял в банке 1 млн
рублей в кредит.
Схема выплаты кредита следующая: 31 декабря каждого
следующего года банк начисляет проценты на оставшуюся сумму долга (то есть увеличивает долг на определенное количество процентов), затем Арсений переводит очередной транш. Арсений выплатил кредит за два транша, переведя в первый раз 550 тыс. рублей, во второй - 638,4 тыс. рублей. Под какой процент банк выдал кредит Арсению?
Слайд 29Решение
Пусть сумма кредита равна S, годовые составляют a%, первая выплата
X, а вторая Y. Тогда 31 декабря каждого года оставшаяся
сумма долга умножается на коэффициентb=1+0,01a
После первой выплаты сумма долга составит
S1=S*b-X
После второй выплаты сумма долга составит
S2 = S1*b-Y = (S*b)*b-Y = S*b2-X*b-Y
Слайд 31Кризис
В 2015 году ставка по вкладам в банках значительно возросла.
Моя
бабушка решила сделать вклад в 300.000 рублей. В связи с
кризисом мы стали искать самые выгодные предложения по вкладам. Мы выделили 4 банка:Промсвязьбанк – ставка 18% на 5 месяцев;
ВТБ 24 – ставка 20% на 6 месяцев;
Россельхозбанк– ставка 19% на 4 месяца;
Сбербанк – ставка 17% на 8 месяцев; Где выгоднее будет сделать вклад?
Слайд 32Решение
Рассчитаем конечную сумму вклада по истечению срока вложения.
Промсвязьбанк имеет ставку
18% = 0,18 на 5 месяцев, т.е 5/12 года
(300.000+300.000*0,18)*(5/12)=147.500
Аналогично,
проведем расчеты для оставшихся трех банков(300.000+300.000*0,2)*(1/2)=180.000 – ВТБ 24
(300.000+300.000*0,19)*(1/3)=119.000 – Россельхозбанк
(300.000+300.000*0,17)*(2/3)=234.000 – Сбербанк
Таким образом, самым выгодным предложением является вклад в Сбербанк.
Ответ:Сбербанк
Слайд 33Применение
Как известно из практики с помощью процентов часто показывают изменение
той или иной величины
В наше время почти во всех областях
деятельности встречаются проценты
Слайд 34Заключение
Сейчас мы находимся в возрасте, когда нужно выбрать свою профессию
в будущем. В этом году мы все будем сдавать экзамен
в формате ЕГЭ, где есть задания с процентными вычислениями. 90% из нашего выпуска будут поступать в вузы, где будет требоваться знания математики, а без знаний экономического счета и вычисления процентов поступить может быть сложно. Знания о процентах так же помогут нам и на других предметах, например, химии и, конечно же, в быту.
