Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Golden ratio
Содержание
- 1. Golden ratio
- 2. What is Golden Ratio? The Golden Ratio is
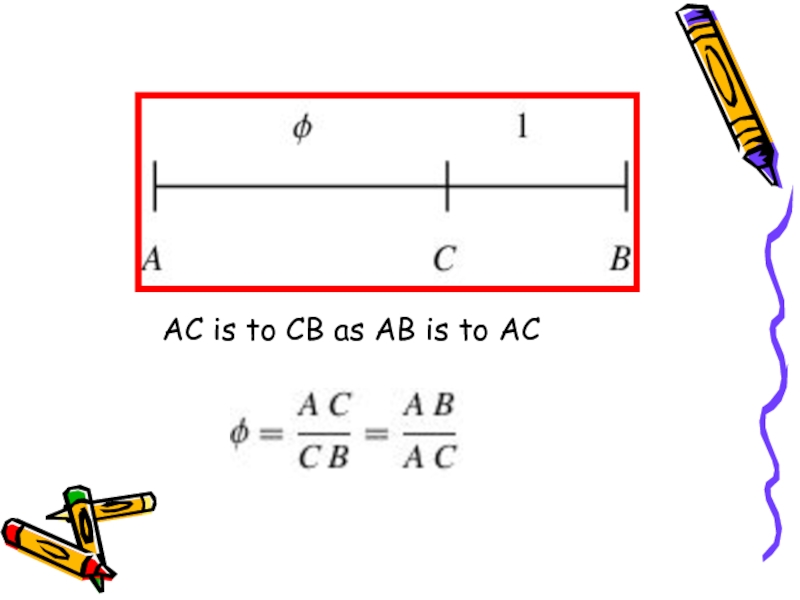
- 3. AC is to CB as AB is to AC
- 4. What is the Fibonacci Sequence of Numbers?
- 5. Relationship between the Fibonacci Sequence and the
- 6. As we can see, the ratio approaches
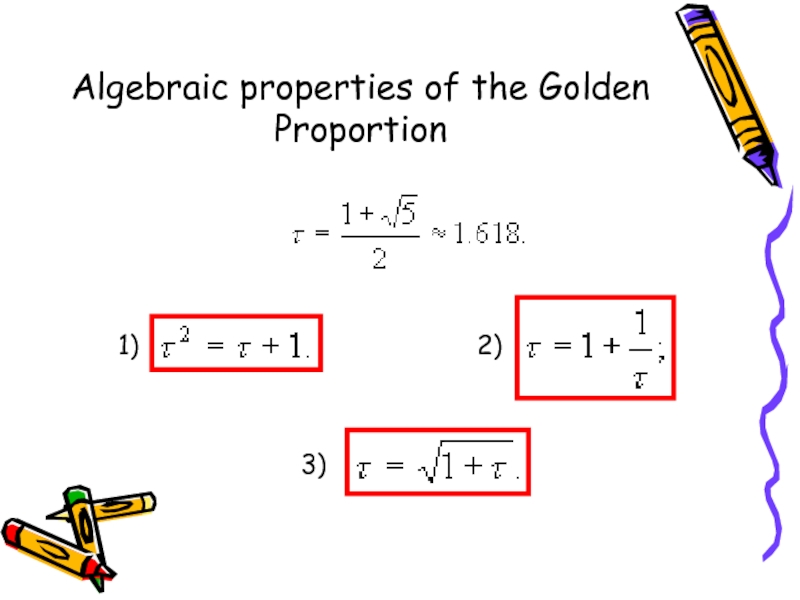
- 7. Algebraic properties of the Golden Proportion1)2)3)
- 8. Constructing a Golden Rectangle Given:
- 9. Golden triangle The golden triangle is an isosceles
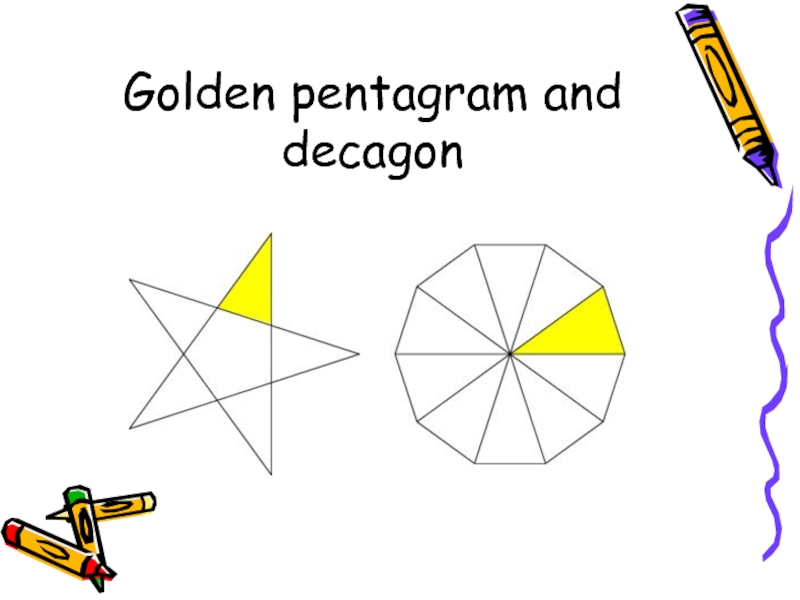
- 10. Golden pentagram and decagon
- 11. Plants growth The branching rates in plants occur
- 12. Flowers On the back of the passiflora incarnate,
- 13. Petal counts The petals of the different flowers
- 14. The Golden Ratio in Humans Dr. Stephen Marquardt
- 15. The Human Smile A perfect smile: the front
- 16. The Golden Ratio in Arts The Golden Ratio
- 17. Mona Lisa Mona Lisa's face is a perfect
- 18. The last supper The masterpiece "Last Supper," contains
- 19. Statue of Athena In the Statue of Athena,
- 20. The Golden Ratio in Architecture The Golden Ratio
- 21. The Great Pyramid at Giza Half of
- 22. The Parthenon The exterior dimensions of the
- 23. The UN Building In the United Nations
- 24. Conclusion From the ancient times people were looking
- 25. Скачать презентанцию
What is Golden Ratio? The Golden Ratio is a unique number, approximately 1.618033989. It is also known as the Divine Ratio, the Golden Mean, the Golden Number, and the Golden Section.
Слайды и текст этой презентации
Слайд 4What is the Fibonacci Sequence of Numbers?
The Fibonacci numbers are
a unique sequence of integers, starting with 1, where each
element is the sum of the two previous numbers. For example: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, etc.Слайд 5Relationship between the Fibonacci Sequence and the Golden Ratio
The Fibonacci
Sequence is an infinite sequence, which means it goes on
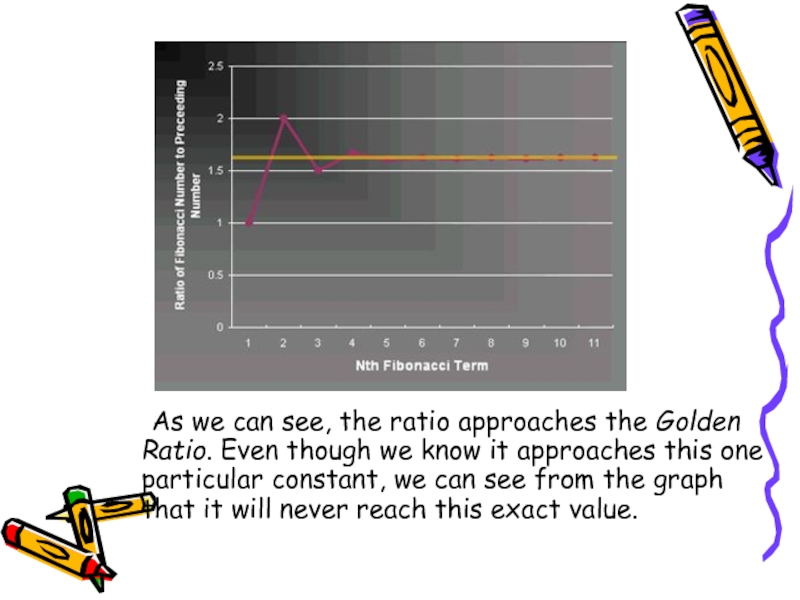
for ever, and as it develops, the ratio of the consecutive terms converges (becomes closer) to the Golden Ratio, ~1.618. For example, to find the ratio of any two successive numbers, take the latter number and divide by the former. So, we will have: 1/1=1, 2/1=2, 3/2=1.5, 5/3=1.66, 8/5=1.6, 13/8=1.625, 21/13=1.615.Слайд 6 As we can see, the ratio approaches the Golden Ratio.
Even though we know it approaches this one particular constant,
we can see from the graph that it will never reach this exact value.Слайд 8
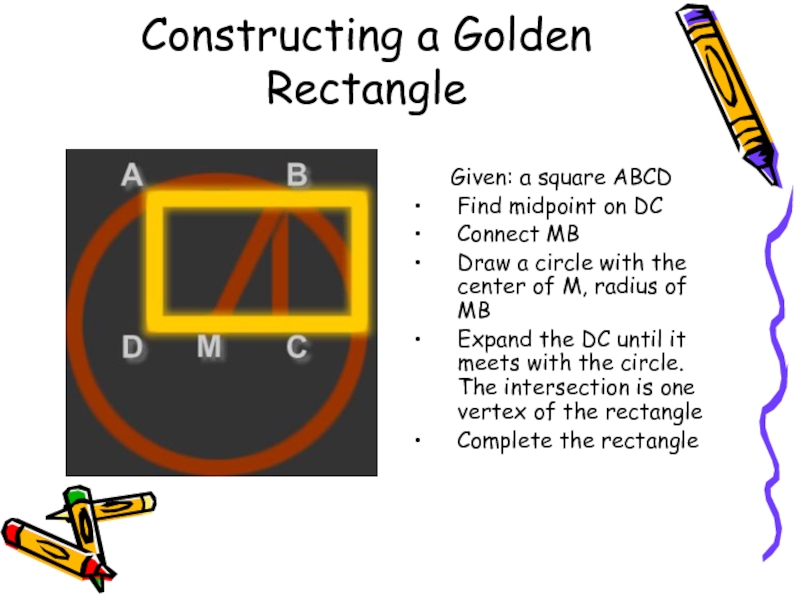
Constructing a Golden Rectangle
Given: a square ABCD
Find midpoint on DC
Connect
MB
Draw a circle with the center of M, radius of
MB Expand the DC until it meets with the circle. The intersection is one vertex of the rectangle
Complete the rectangle
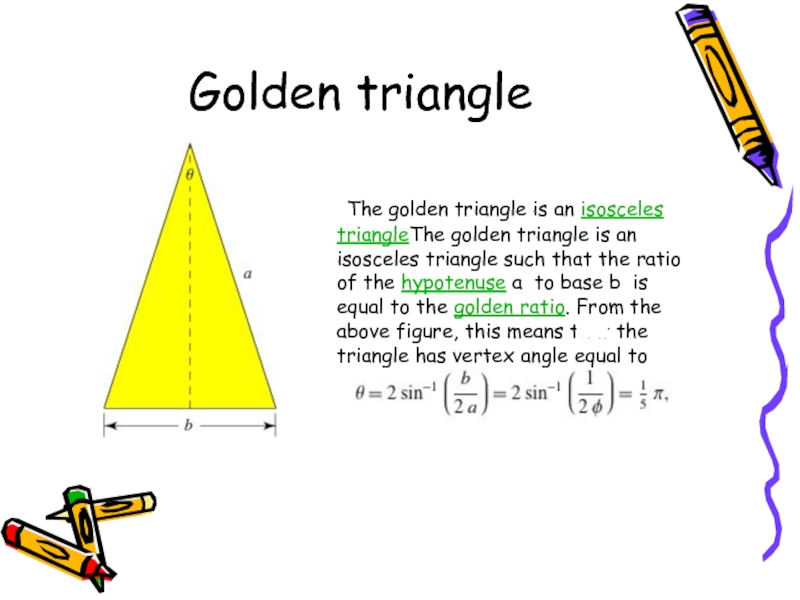
Слайд 9Golden triangle
The golden triangle is an isosceles triangleThe golden triangle
is an isosceles triangle such that the ratio of the
hypotenuse a to base b is equal to the golden ratio. From the above figure, this means that the triangle has vertex angle equal toСлайд 11Plants growth
The branching rates in plants occur in the Fibonacci
pattern, where the first level has one "branching" (the trunk),
the second has two branches, than 3, 5, 8, 13 and so on. Also, the spacing of leaves around each branch or stalk spirals with respect to the Golden Ratio.Слайд 12Flowers
On the back of the passiflora incarnate, the 3 sepals
(the part of the flower that is not the petal)
that protected the bud are outermost, followed by the 5 outer green petals and an inner layer of 5 more paler green petals.
Слайд 13Petal counts
The petals of the different flowers also contain the
Fibonacci Numbers. The examples are that the buttercup has 5
petals, delphiniums has 8 petals, ragwort has 13 petals, aster as 21 petals, plantain has 34 petals, and asteraceae family has 55 petals, and some of them have 89 petals.Слайд 14The Golden Ratio in Humans
Dr. Stephen Marquardt is a former
plastic surgeon, has used the golden section and some of
its relatives to make a mask that he claims that is the most beautiful shape a human face can ever have, it used decagons and pentagons as its function that embodies phi in all their dimensions.Слайд 15The Human Smile
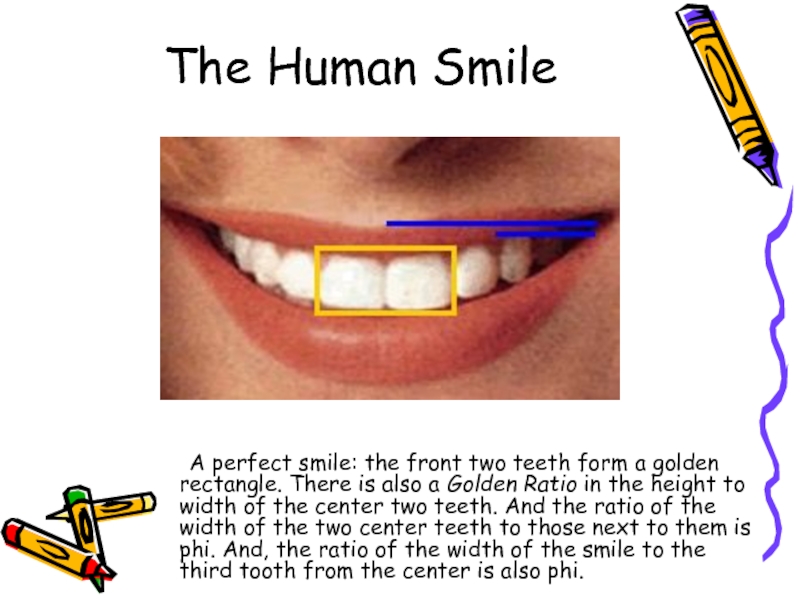
A perfect smile: the front two teeth form
a golden rectangle. There is also a Golden Ratio in
the height to width of the center two teeth. And the ratio of the width of the two center teeth to those next to them is phi. And, the ratio of the width of the smile to the third tooth from the center is also phi.Слайд 16The Golden Ratio in Arts
The Golden Ratio has a great
impact on art, influencing artists' perspectives of a pleasant art
piece. Da Vinci, a sculpture, a painter, an inventor and a mathematician, was the first one who first called Phi the Golden Ratio.Слайд 17Mona Lisa
Mona Lisa's face is a perfect golden rectangle, according
to the ratio of the width of her forehead compared
to the length from the top of her head to her chin.Слайд 18The last supper
The masterpiece "Last Supper," contains a golden ratio
in several places, appearing in both the ceiling and the
position where the people sit.Слайд 19Statue of Athena
In the Statue of Athena, the first Golden
Ratio is the length from the front head to the
ear opening compared with the length from the forehead to the chin. The second one appears in the ratio of the length from the nostril to the earlobe compare with the length from the nostril to the chin.Слайд 20The Golden Ratio in Architecture
The Golden Ratio has appeared in
ancient architecture. Not only did the ancient Egyptians and Greeks
know about the magic of Golden Ratio, so did the Renaissance artists, who used the Golden Ratio in the design of Notre Dame in between the 12th and 14th centuries.Слайд 21The Great Pyramid at Giza
Half of the base, the slant
height, and the height from the vertex to the center
create a right triangle.Слайд 22The Parthenon
The exterior dimensions of the Parthenon form a Golden
Ratio in many of the proportions.
Слайд 23The UN Building
In the United Nations building, the width of
the building compared with the height of every ten floors
is a Golden Ratio.Слайд 24Conclusion
From the ancient times people were looking for harmony and
perfection. Ancient Greeks considered that the world can’t be without
laws of harmony and the searching of harmony is the way of learning the world.Golden ratio makes an impression of harmony and beauty. That’s why sculptors, architects and artists use golden ratio in their works.
Теги