Quadratic equations/ Квадратты? те?деу

теңдеулер
Root - түбір
properties of a quadratic equation – квадрат түбірдің

қасиеттері
sum square – екі өрнектің қосындысының
difference of two expressions- айырымының квадраты
real numbers – нақты сандар
A – the first coefficient – бірінші коэффициент
B – the second coefficient- екінші коэффициент
C - constant term – бос мүше
Graph - граф
Parabola – парабола
IF- мұндағы

in the form ax2+bx+c=0, where a,b and c are real

numbers and a ≠0
A – the first coefficient
B – the second coefficient
C - constant term
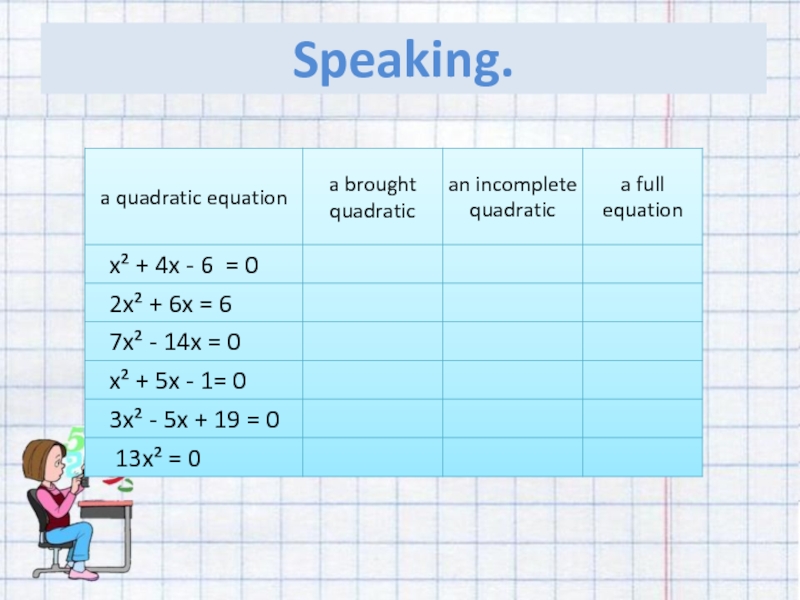
If in the equation b≠0,c≠0 , then it is called a full equation (толық квадрат теңдеу)
If in a full quadratic equation a=1, it is called brought quadratic the equation (келтірілген квадрат теңдеу)
If b or c, or both are equal to zero, then the equation is called as an incomplete quadratic equation

quadratic equations
Their solution in Ancient Babylon was closely connected with

practical problems, mainly such as the measurement of land, land work related to military needs; the presence of these knowledge is also due to the development of mathematics and astronomy in general. There have been known methods of solving both full and incomplete quadratic equations. We give examples of quadratic equations, is solved in ancient Babylon, using modern algebraic entry

on astronomy "Ariabhattiam" written by an Indian astronomer and mathematician

Aryabhata in 499 AD. One of the first conclusions of the formula known roots of a quadratic equation belongs to an Indian scientist Brahmagupta (about 598 g.) [1]; Brahmagupta stated universal rule solving a quadratic equation, the given to the canonical form: ax ^ 2 + bx = c; moreover, it was assumed that all the coefficients in it than a, may be negative. Scientists formulated a rule in essence the same as the modern.

тәсілімен 2-топ. Екімүшенің квадратын  айырып алу әдісімен 3-топ. Формула арқылы шешу тәсілімен 4-топ.басқа

әдістермен

–2х2-5х+7=0     
2. 5х2=0     
3. 3х²+9х=0                      
4. х2– 49=0



3-топ.                                                       -    
1) 4х²=0                                              
2) х²-25=0                                              

3)3х²-6х=0                                             
4)8х²-4х+5=0              
4-топ.
1) -2х²=0
2)  х²-64=0
3)  2у+у²=0
4)х²+6х-19=0

4) Х1=-4; Х2=3                                  

2-топ.
1) Х1=1; Х2=-3,5
2) Х=0
3)    Х1=0;

Х2=-3                                          
4) Х1=-7; Х2=7


3-топ.                                                       -    
1) 0
2) Х1=5; Х2=-5
3)    Х1=0; Х2=2                                          
4) шешімі жоқ
             
4-топ.
1) 0
2) Х1=8; Х2=-8
3)    Х1=0; Х2=2                                          
4) х=-3

В. С. 2,5 ; 105 D

. 2. Еге р a,b,c-ның а=5, b=2, с= -3-ның мәндері белгілі болса, онда ax2+bx+c=0 теңдеуін құрындар: А. -5х2-2х+3=0; B. 5х2-2х+3=0; С. 5х2+2х-3=0; D. х2+2х-3=0 3. 5х2-20=0 А. Х1=2; Х1=-2; В. Х1=4; Х1=-4; С. Х1=0; Х1=2; D.Х1=2; Х1=4; 4. 3х2-2х-1=0 теңдеуіндегі а-ның мәні неге тең? А. 2; В. 3; С. -3; D. 1; 5. Келтірілген теңдеудегі а-ның мәні неге тең? А. 0; В. 2; С. -1; D. 1;   II нұсқа Теңдеуді шешіңіз: (2х+3)(6-3х)=0 А. -1,5; 2 В. 1;0 С. 3;6 D. 1,2;2 2. Егер a,b,c-ның а=3, b=-2, с= 1-ның мәндері белгілі болса, онда ax2+bx+c=0 теңдеуән құрындар: А. х2-2х+1=0; B. 3х2-2х-1=0; С. -3х2+2х-1=0; D. 3х2-2х+1=0 3. 2х2-8=0 А. Х1=4; Х1=-4; В. Х1=2; Х1=-2; С. Х1=0; Х1=2; D.Х1=2; Х1=4; 4. 6х2-5х-1=0 теңдеуіндегі b -ның мәні неге тең? А. 2; В. 5; С. -5; D. 1; 5. Квадрат теңдеудің дәрежесі неге тең? А. 0; В. 1; С. -1; D. 2;

Д
3. В
4. С
5. Д