Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определение расстояний до тел Солнечной системы и размеров этих тел
Содержание
- 1. Определение расстояний до тел Солнечной системы и размеров этих тел
- 2. 1. Геометрический метод (по параллаксам)В – точка,
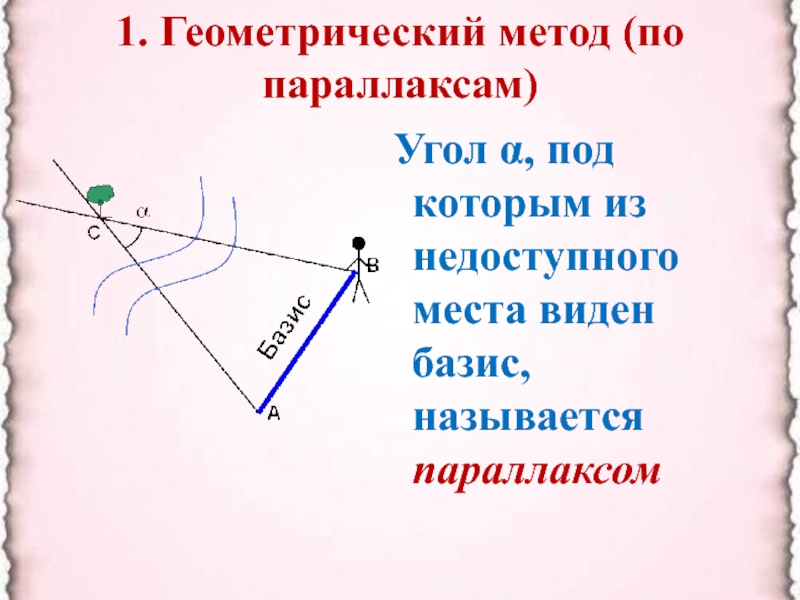
- 3. 1. Геометрический метод (по параллаксам) Угол α, под которым из недоступного места виден базис, называется параллаксом
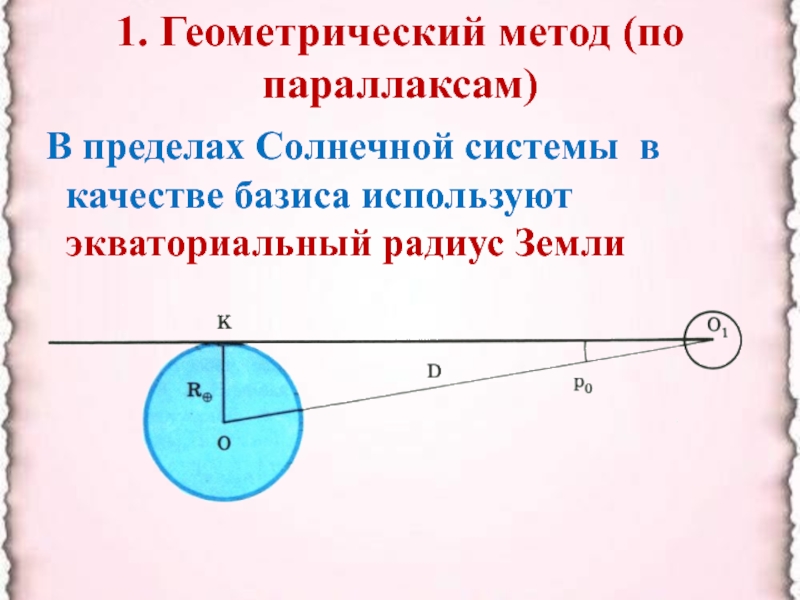
- 4. 1. Геометрический метод (по параллаксам) В пределах
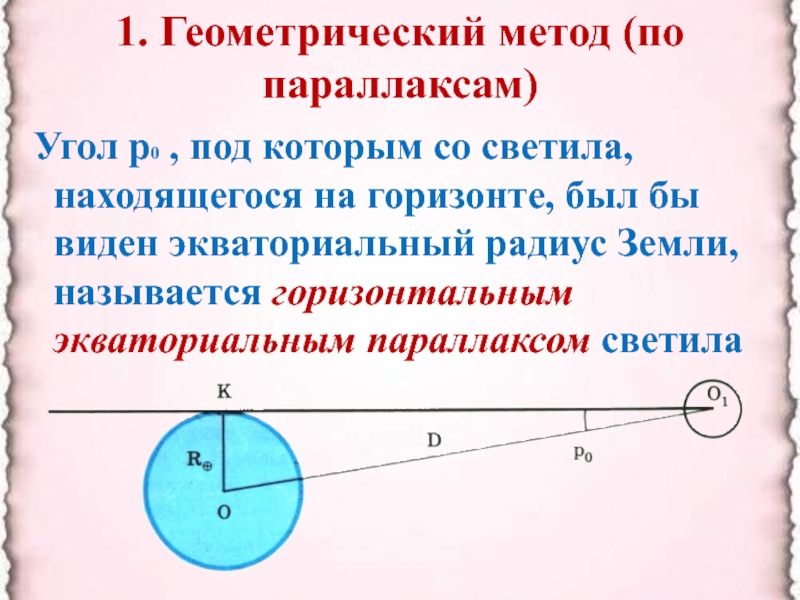
- 5. 1. Геометрический метод (по параллаксам) Угол р0
- 6. 1. Геометрический метод (по параллаксам) Если горизонтальный
- 7. 1. Геометрический метод (по параллаксам) Поскольку углы
- 8. 1. Геометрический метод (по параллаксам) Тогда:
- 9. 2. Радиолокационный метод Радиолокация заключается в том,
- 10. 2. Радиолокационный метод Зная скорость света в
- 11. 2. Радиолокационный метод Радиолокационные наблюдения позволяют с
- 12. 3. Лазерная локация Метод аналогичен радиолокации,
- 13. 4. Определение размеров тел Солнечной системы При
- 14. 4. Определение размеров тел Солнечной системы
- 15. 4. Определение размеров тел Солнечной системы Учитывая ранее полученную формулу для D, получим:
- 16. 4. Определение размеров тел Солнечной системы А так как углы малы, то:
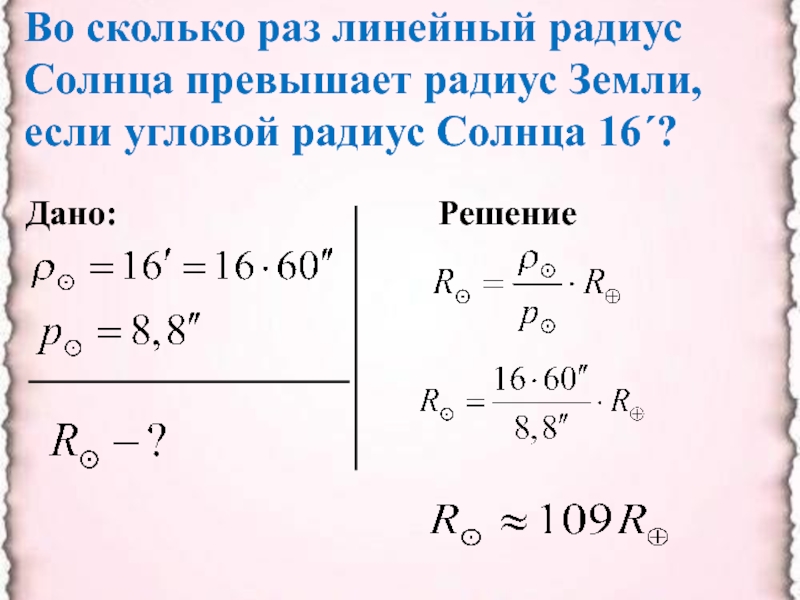
- 17. Во сколько раз линейный радиус Солнца превышает
- 18. Спасибо за внимание!
- 19. Скачать презентанцию
1. Геометрический метод (по параллаксам)В – точка, в которой находится наблюдатель;А – доступная точка;С – недоступная точкаАВ – базис (измеряется непосредственно)Углы измеряются геодезическим инструментом
Слайды и текст этой презентации
Слайд 1Определение
расстояний
до тел
Солнечной системы
и размеров
этих тел
Учитель
физики ВКК
Валериевна
Слайд 21. Геометрический метод (по параллаксам)
В – точка, в которой находится
наблюдатель;
А – доступная точка;
С – недоступная точка
АВ – базис (измеряется
непосредственно)Углы измеряются геодезическим инструментом
Слайд 31. Геометрический метод (по параллаксам)
Угол α, под которым из
недоступного места виден базис, называется параллаксом
Слайд 41. Геометрический метод (по параллаксам)
В пределах Солнечной системы в
качестве базиса используют экваториальный радиус Земли
Слайд 51. Геометрический метод (по параллаксам)
Угол р0 , под которым
со светила, находящегося на горизонте, был бы виден экваториальный радиус
Земли, называется горизонтальным экваториальным параллаксом светила
Слайд 61. Геометрический метод (по параллаксам)
Если горизонтальный параллакс найден, то
расстояние до светила вычисляется по формуле:
где D
– расстояние от центра Земли до центра какого либо тела Солнечной системы;‒ экваториальный радиус Земли
Слайд 71. Геометрический метод (по параллаксам)
Поскольку углы р0 очень малы,
то их синусы можно заменить самими углами, если величина угла
выражена в радианах: но обычно р0 выражено в секундах дуги, поэтому:
Слайд 81. Геометрический метод (по параллаксам)
Тогда:
Параллакс выражен в
секундах дуги,
а D – либо в километрах, либо в
радиусах Земли
Слайд 92. Радиолокационный метод
Радиолокация заключается в том, что на небесное
тело посылают мощный кратковременный радиоимпульс, а потом принимают отраженный сигнал
Слайд 102. Радиолокационный метод
Зная скорость света в вакууме:
с
= 299 792 458 м/с
и точно измерив
время прохождения сигнала туда и обратно, легко вычислить расстояние до небесного тела
Слайд 112. Радиолокационный метод
Радиолокационные наблюдения позволяют с большой точностью определять
расстояния до небесных тел Солнечной системы.
Этим методом уточнены
расстояния до Луны, Венеры, Меркурия, Марса, Юпитера
Слайд 123. Лазерная локация
Метод аналогичен радиолокации, однако точность гораздо
выше.
Лазерная локация позволяет определять расстояния между точками лунной и
земной поверхности с точностью до сантиметров 
Слайд 134. Определение размеров тел Солнечной системы
При наблюдениях небесных тел
Солнечной системы можно измерить угол ρ, под которым они видны
земному наблюдателю
Слайд 144. Определение размеров тел Солнечной системы
Зная этот угловой
радиус светила ρ и расстояние до светила D, можно вычислить
линейный радиус R:
Слайд 154. Определение размеров тел Солнечной системы
Учитывая ранее полученную формулу
для D, получим:
Слайд 17Во сколько раз линейный радиус Солнца превышает радиус Земли, если
угловой радиус Солнца 16´?
Дано:
Решение
