Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основные направления эконофизики. Фрактальный анализ финансовых рядов
Содержание
- 1. Основные направления эконофизики. Фрактальный анализ финансовых рядов
- 2. Эконофизика. Этапы развития199519972001 20022009НастоящеевремяПоявление термина для обозначения
- 3. План доклада История науки о финансовых временных рядахАнализ
- 4. Финансовые временные ряды. История. Динамический подход.90-е
- 5. Финансовые временные ряды. История. Стохастический подход.
- 6. Финансовые временные ряды История. Стохастический подход
- 7. Финансовые временные ряды История. Стохастический подход
- 8. Распределение Леви (Levi, 1925) Общий вид устойчивого распределения:
- 9. Распределение Леви
- 10. Индекс S&P 500 (пятисот крупнейших по капитализации американских компаний) за период с 1984 по 1996 гг.
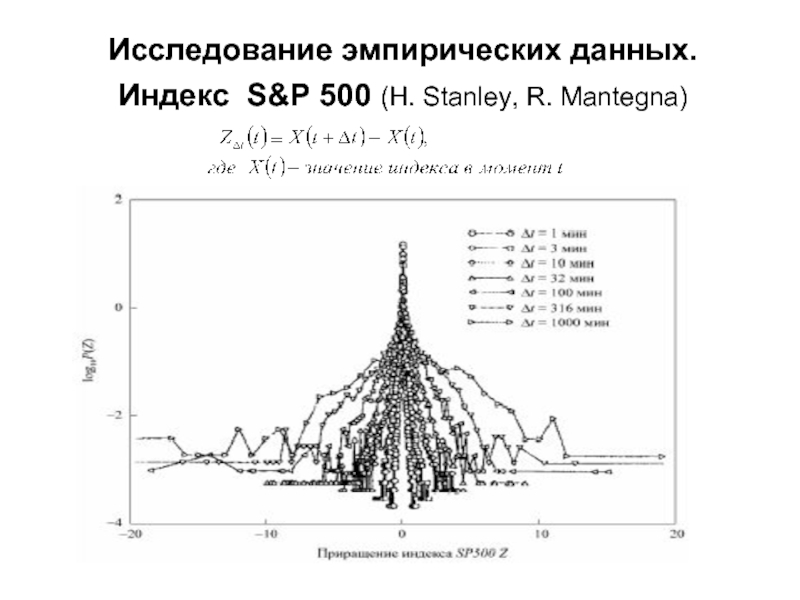
- 11. Исследование эмпирических данных. Индекс S&P 500
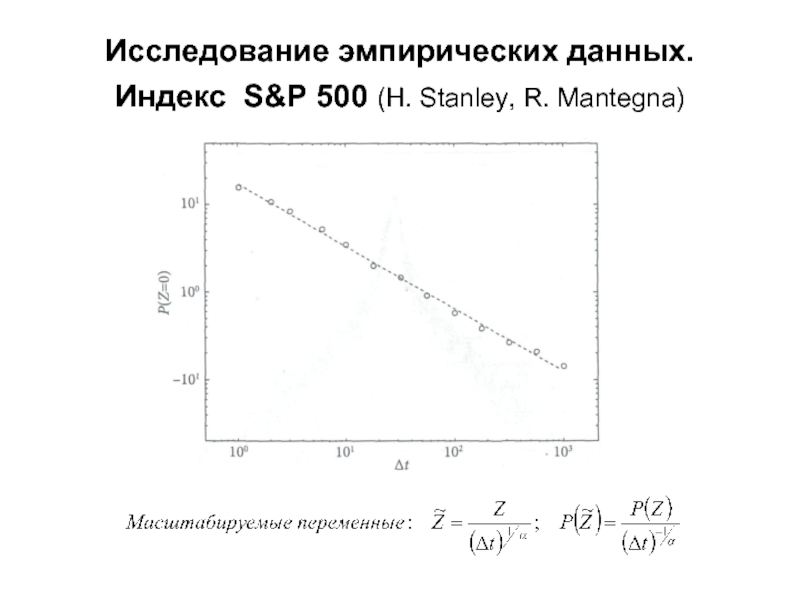
- 12. Исследование эмпирических данных. Индекс S&P 500 (H. Stanley, R. Mantegna)
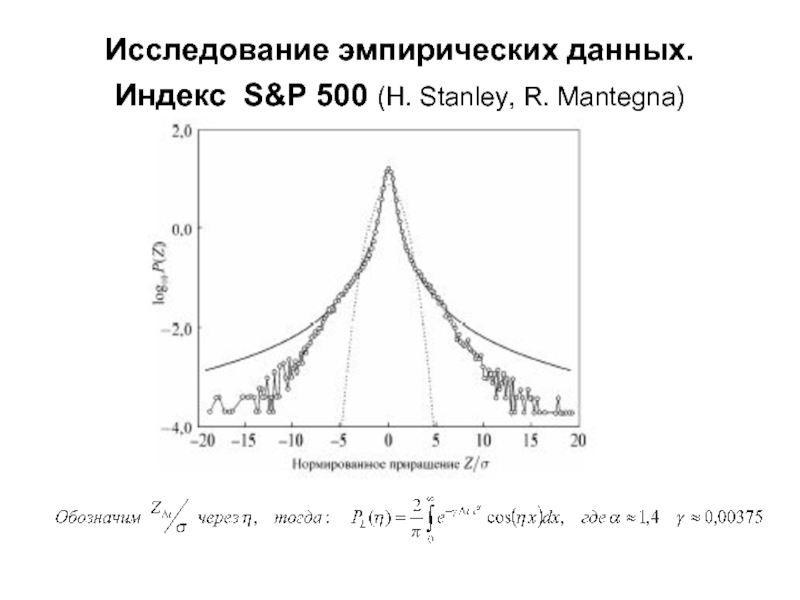
- 13. Исследование эмпирических данных. Индекс S&P 500 (H. Stanley, R. Mantegna)
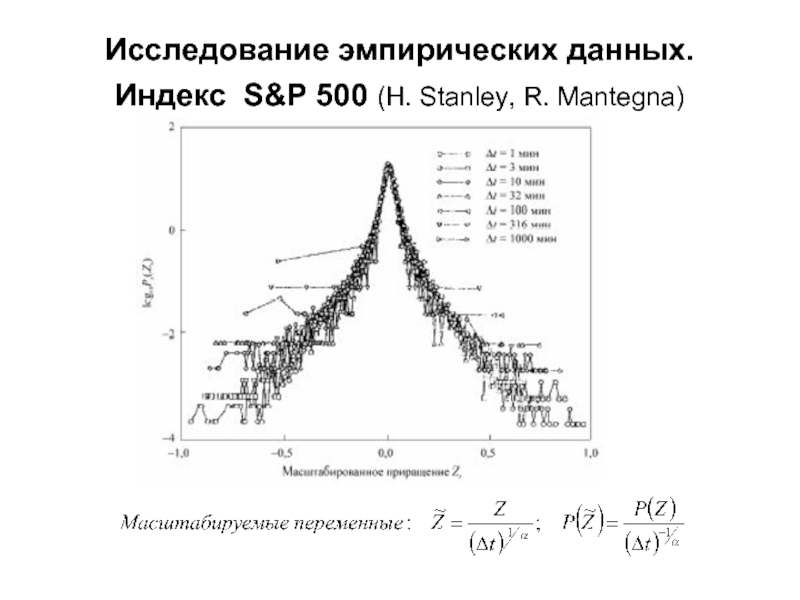
- 14. Исследование эмпирических данных. Индекс S&P 500 (H. Stanley, R. Mantegna)
- 15. Исследование эмпирических данных редких событий (P. Gopikrishnan, V. Plerou, H. Stanley)
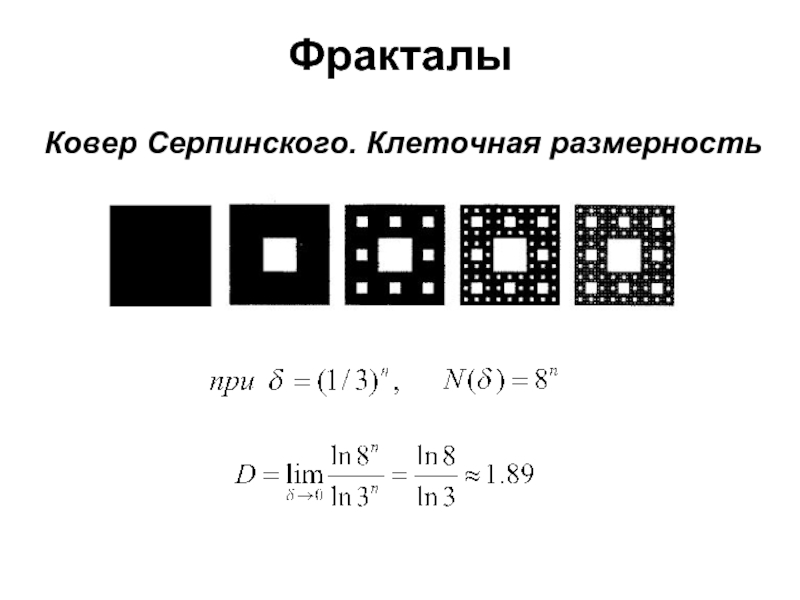
- 16. ФракталыОпределение размерности (F. Hausdorff, 1919) (для компактного множества в произвольномметрическом пространстве)Мотивация:(D=1,2,3)
- 17. Фракталы Фрактал – это множество, для которого хаусдорфова
- 18. ФракталыКривая Коха. Внутренняя размерность.
- 19. ФракталыБереговая линия Британии (L.F. Richardson, 1961)
- 20. Отличия природных фракталов от модельныхВо-первых, естественные фракталы
- 21. ФракталыФинансовые временные ряды Движения цен большинства финансовых инструментов
- 22. ФракталыФинансовые временные рядыКлеточная размерностьФракталы
- 23. При H 0,5 – временной
- 24. ФракталыФинансовые временные ряды. Показатель Херста HФракталы
- 25. ФракталыКовер Серпинского. Клеточная размерность
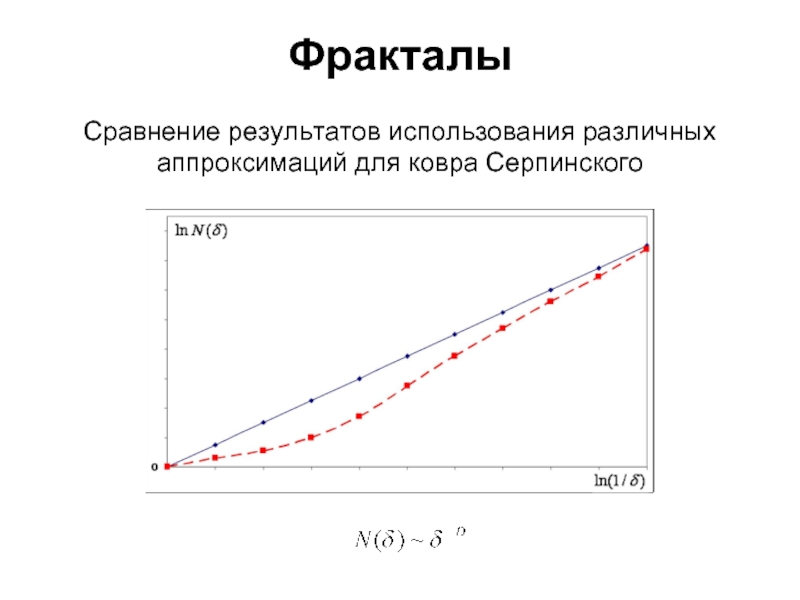
- 26. ФракталыСравнение результатов использования различных аппроксимаций для ковра Серпинского
- 27. ФракталыФинансовые временные ряды. Асимптотика для площади покрытий
- 28. ФракталыФинансовые временные ряды Размерность минимального покрытия Индекс
- 29. ФракталыФинансовые временные ряды Размерность минимального покрытия Индекс фрактальности
- 30. Фрактальный анализ финансовых временных рядов. Быстрый выход на степенную асимптотику
- 31. Фрактальный анализ финансовых временных рядов. Быстрый
- 32. Фрактальный анализ финансовых временных рядов. Типичное поведение ряда и функции
- 33. Фрактальный анализ финансовых временных рядов. Распределения вероятности
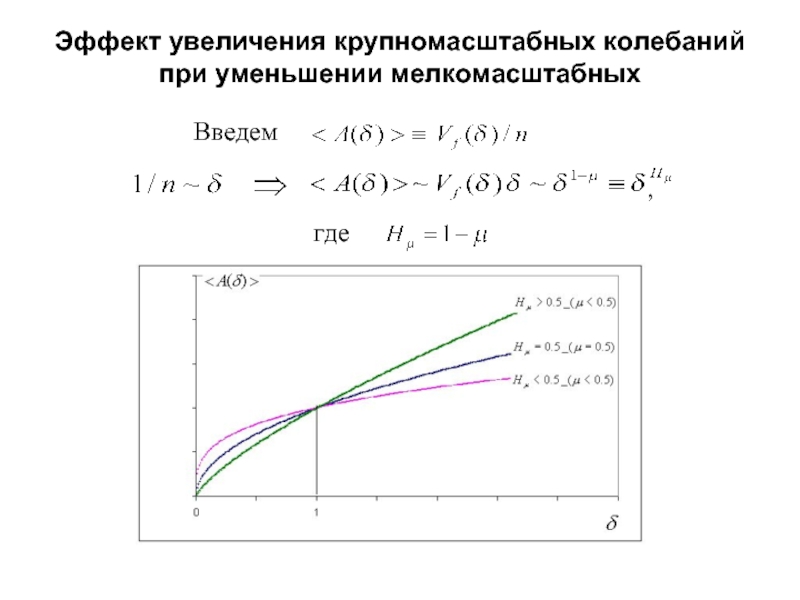
- 34. Эффект увеличения крупномасштабных колебаний при уменьшении мелкомасштабных Введемгде,
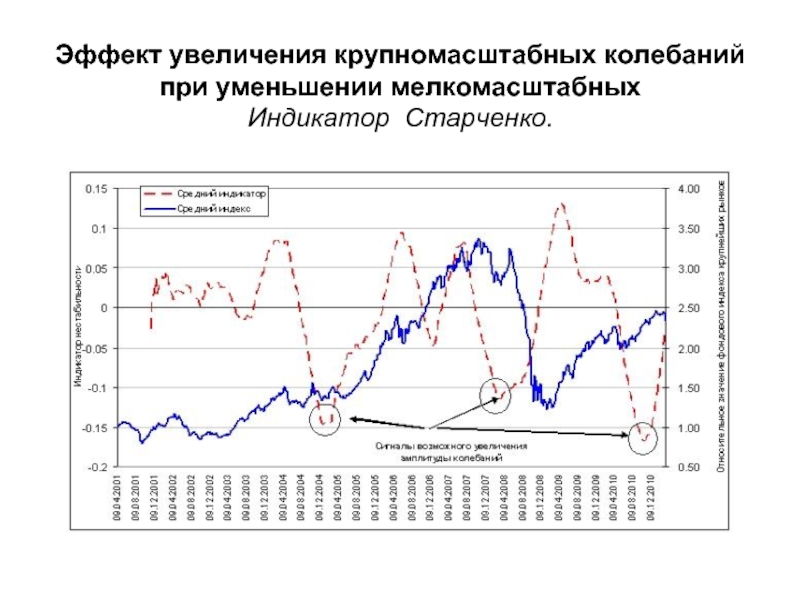
- 35. Эффект увеличения крупномасштабных колебаний при уменьшении мелкомасштабных Индикатор Старченко.
- 36. Модели обвалов на финансовом рынке1. Инвесторы и
- 37. Модели обвалов на финансовом рынке 2. a) Решетчатые модели. Модель Изинга. Перколяция.
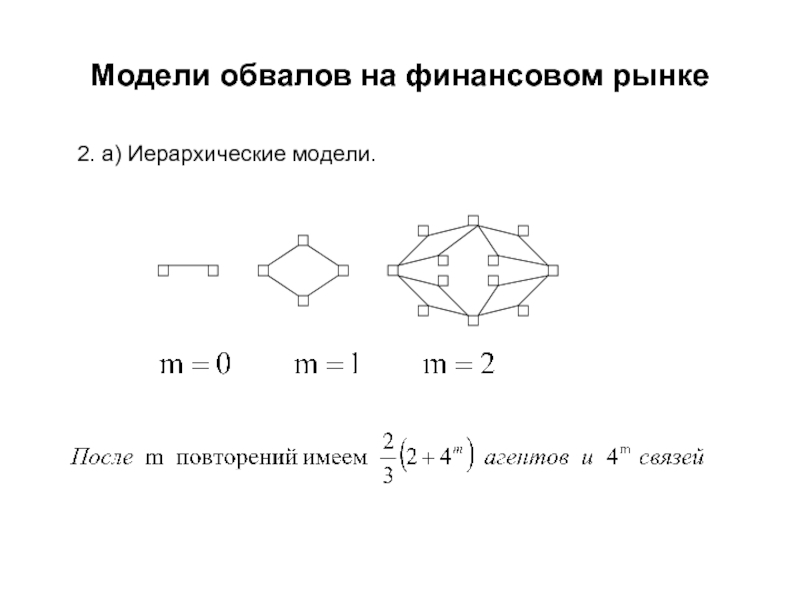
- 38. Модели обвалов на финансовом рынке 2. a) Иерархические модели.
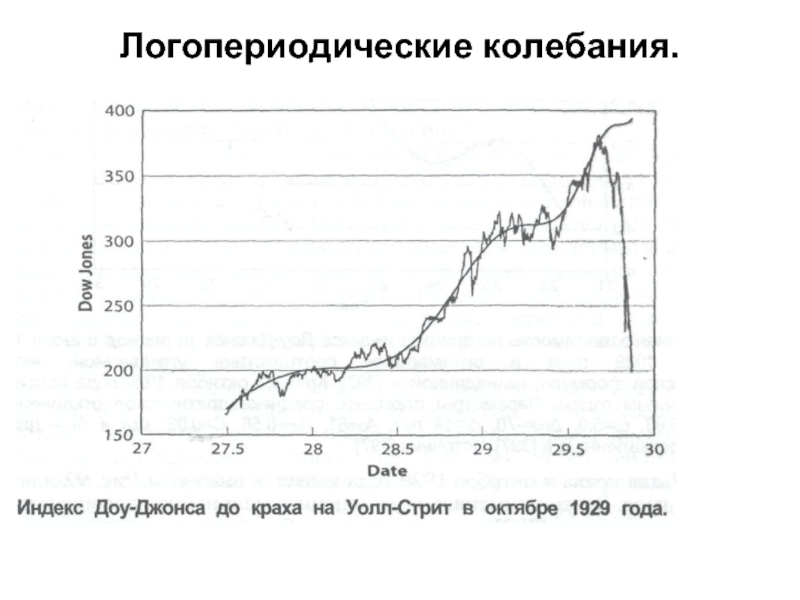
- 39. Модели обвалов на финансовом рынке 2. a) Иерархические модели. Логопериодические колебания.
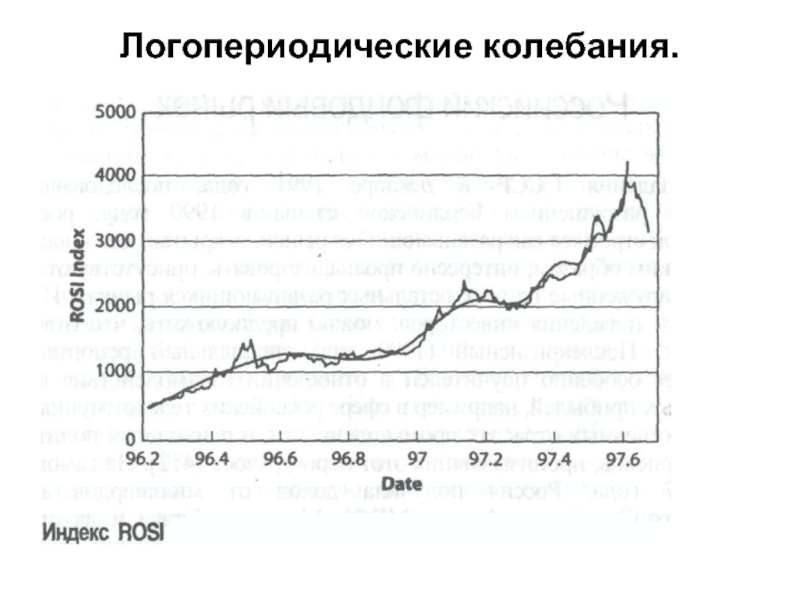
- 40. Логопериодические колебания.
- 41. Логопериодические колебания.
- 42. Minority GameМодели взаимодействующих агентов K
- 43. Minority Game (Arthur W.B., Challet D., Lux T., Marsili M., Zhang Y-C)
- 44. Minority Game (Arthur W.B., Challet
- 45. Другие разделы экономики: 1. Распределение богатства (V. Yakovenko,
- 46. Эконофизика и мэйнстрим«Лежащее в основе современной экономической
- 47. Эконофизика и мэйнстрим… Но в Новое Время
- 48. Эконофизика и мэйнстримЭКОНОФИЗИКАИНСТИТУЦИОНАЛЬНАЯ ЭКОНОМИКАМЕЙНСТРИМ
- 49. Литература:1. Мантенья Р.Н., Стенли Г.Ю. Введение в
- 50. Спасибо за внимание
- 51. Скачать презентанцию
Эконофизика. Этапы развития199519972001 20022009НастоящеевремяПоявление термина для обозначения работ специалистов по статфизике в области экономики и финансовWorkshop on Econophysics в Будапеште Первая международная конференция на БалиНачало институциональной фазы развитияПервый всероссийский конгресс в
Слайды и текст этой презентации
Слайд 1Основные направления эконофизики. Фрактальный анализ финансовых рядов
Дубовиков Михаил Михайлович
Директор по
стратегии
Слайд 2Эконофизика. Этапы развития
1995
1997
2001
2002
2009
Настоящее
время
Появление термина для обозначения работ специалистов по
статфизике в области экономики и финансов
Workshop on Econophysics в Будапеште
Первая международная конференция на Бали
Начало институциональной фазы развития
Первый всероссийский конгресс в Москве
Секция эконофизики – неотъемлемая часть многих ежегодных международных и националных конференций по социальным наукам (ESHIA (international Heterogeneous Interacting Agents), AKSOE и др.)
Слайд 3План доклада
История науки о финансовых временных рядах
Анализ эмпирических данных. Универсальные
распределения
Фрактальный анализ финансовых рядов
Агентно – ориентированные модели в финансах
Другие разделы
экономикиЭконофизика и мэйнстрим
Перспективы развития эконофизики в России
Слайд 4Финансовые временные ряды.
История. Динамический подход.
90-е гг. 19 в. –
Формулировка принципов
Ч. Доу (Ch. Dow).
30-е гг. 20 в. –
Утверждение концепции. Создание основ технического анализа (J. Magee, W. Gann, R. Elliott, и т.д.)80-е гг. 20 в. – Использование методов теории динамического хаоса. Теорема Такенса.
(D. Ruelle, F. Takens, N. Packard)
Слайд 5Финансовые временные ряды.
История. Стохастический подход.
L. Bachelier (1900)
ПЕРВЫЙ
ПОСТУЛАТ.
Приращения цены на непересекающихся временных интервалах – независимы.
ВТОРОЙ ПОСТУЛАТ.
Приращения
цены на любом интервале имеют нормальное (гауссово) распределение с плотностьюСлайд 6Финансовые временные ряды
История. Стохастический подход
Отказ от постулата независимости
Fractional Brownian motion (B. Mandelbrot, 1968)
Autoregressive conditional heteroscedasticity,
ARCH (R. F. Engle, 1982)
Слайд 7Финансовые временные ряды
История. Стохастический подход
Отказ от постулата нормальности
(B. Mandelbrot,
1963)
Скейлинговый принцип:
на реальных рынках в условиях
конкуренции
не существует привилегированных временных
интервалов. Это означает, что
Функция доходности
является масштабно-инвариантной.
Вывод: движение цены
описывается «полетом Леви» (Levi
flight)
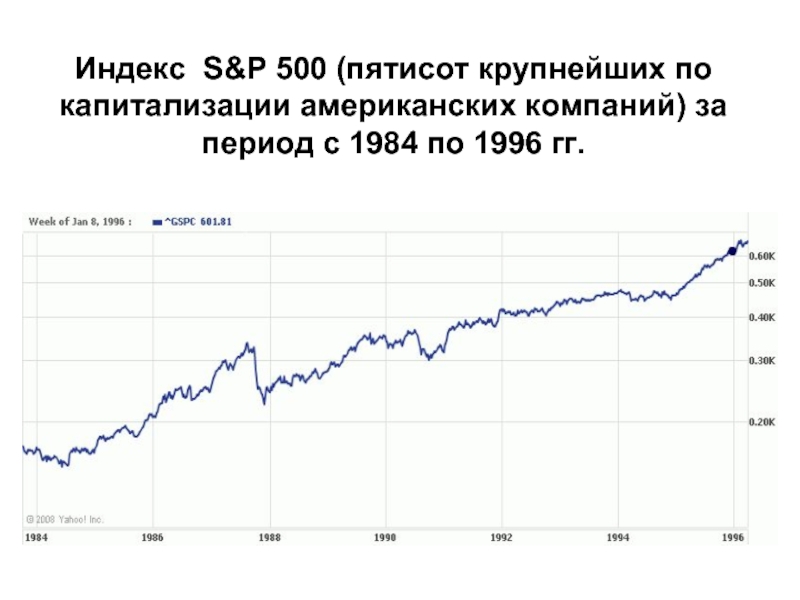
Слайд 10Индекс S&P 500 (пятисот крупнейших по капитализации американских компаний) за
период с 1984 по 1996 гг.
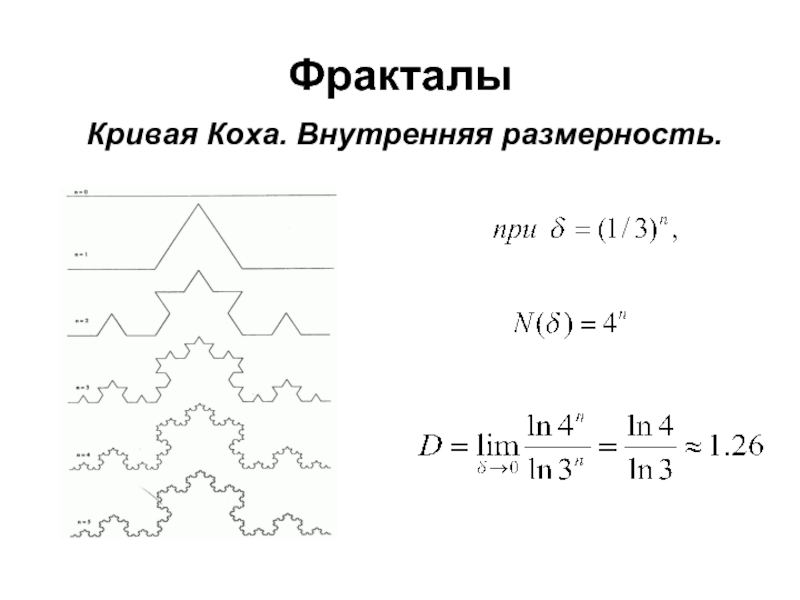
Слайд 16Фракталы
Определение размерности (F. Hausdorff, 1919)
(для компактного множества в произвольном
метрическом
пространстве)
Мотивация:
(D=1,2,3)
Слайд 17Фракталы
Фрактал – это множество, для которого хаусдорфова размерность D строго
больше его топологической размерности DT
Определение (B. Mandelbrot):
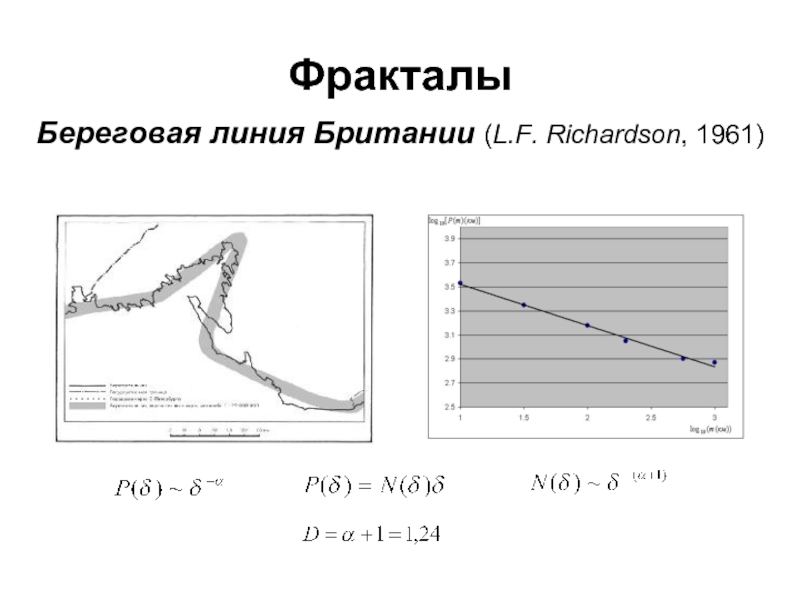
Слайд 20Отличия природных фракталов от модельных
Во-первых, естественные фракталы не бывают строго
симметричными. Свойство же самоподобия для них выполняется лишь в среднем.
Во-вторых, при вычислении размерности естественных фракталов, всегда исключаются масштабы, меньше некоторого минимального масштаба структуры.
В-третьих, для естественных фракталов отсутствует система предфракталов. Поэтому система аппроксимаций симплексами, необходимая для определения размерности, является в общем случае достаточно произвольной.
Слайд 21
Фракталы
Финансовые временные ряды
Движения цен большинства финансовых инструментов внешне похожи, на
разных масштабах времени и цены. По внешнему виду графика наблюдатель
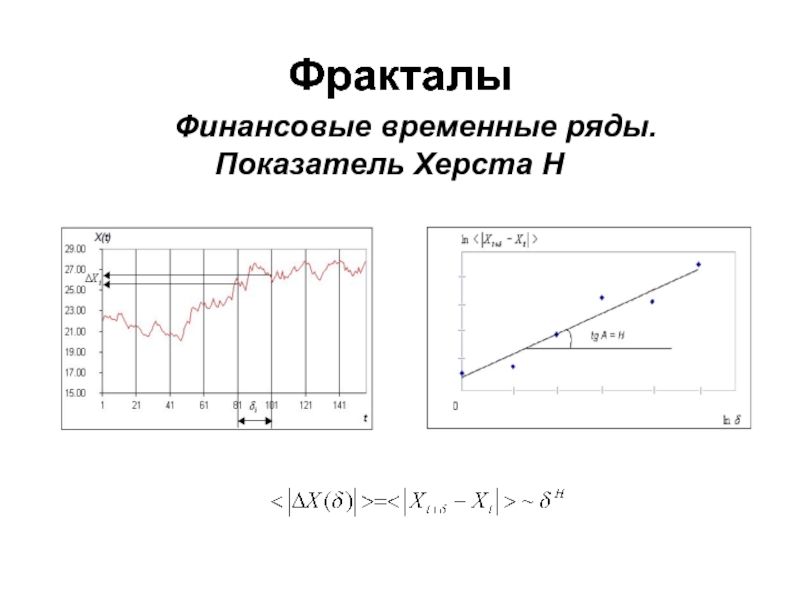
не может сказать, относятся ли данные к недельным, дневным или же часовым изменениям.Слайд 23При H 0,5 – временной ряд находится в
состоянии случайного блуждания При H > 0,5 – наблюдается тренд,
который тем устойчивее, чем больше H При H < 0,5 – наблюдается флэт
Фракталы
Финансовые временные ряды
Показатель Херста H
Для гауссовых случайных процессов
D=2-H
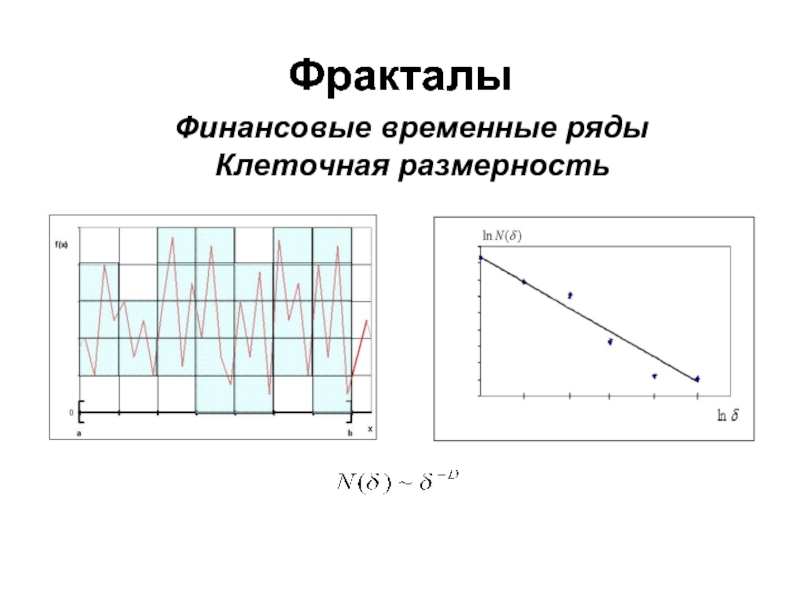
Слайд 28Фракталы
Финансовые временные ряды
Размерность минимального покрытия
Индекс фрактальности
Для функции f(t), определенной на [a,b] введем равномерное разбиение отрезка
и рассмотрим минимальное покрытие графика f(t). Тогда:
Слайд 29Фракталы
Финансовые временные ряды
Размерность минимального покрытия
Индекс фрактальности
Введем
обозначение:
Поскольку
Назовем
- индексом фрактальности
- размерностью минимального покрытия,
где
то
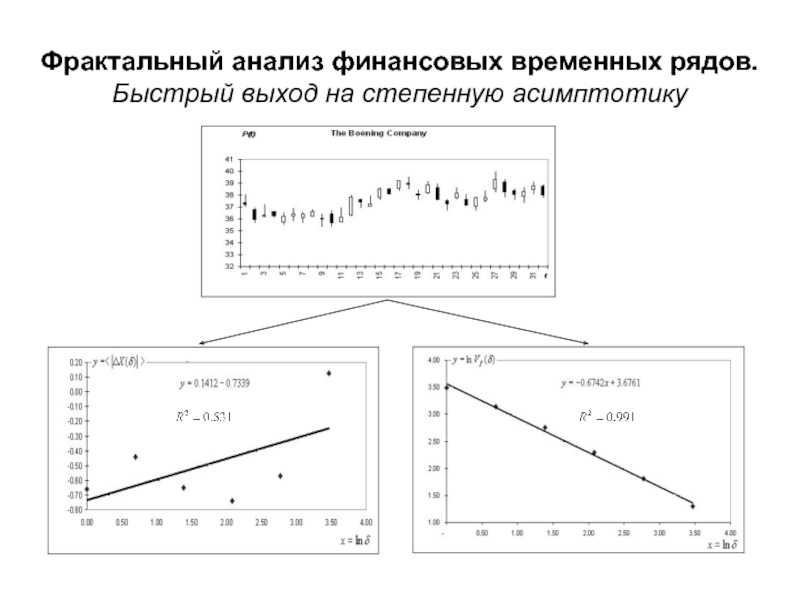
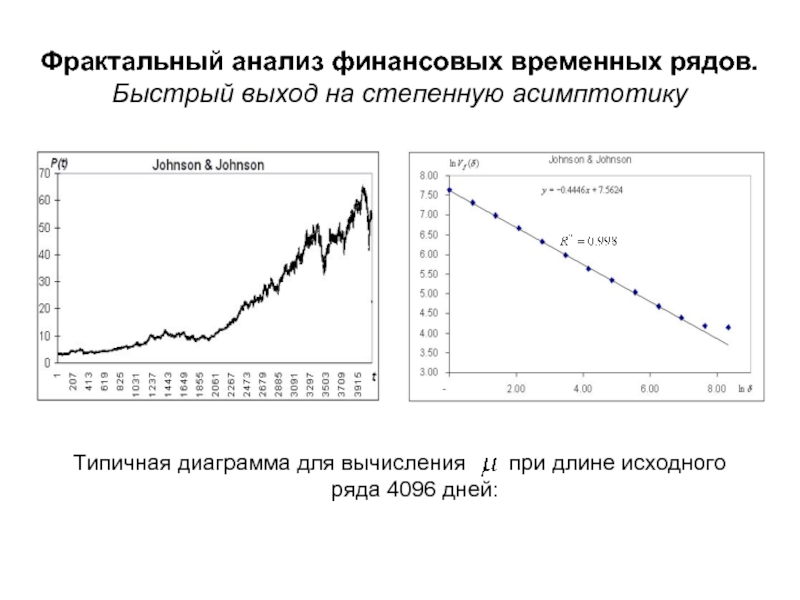
Слайд 31Фрактальный анализ финансовых временных рядов. Быстрый выход на степенную
асимптотику
Типичная диаграмма для вычисления при длине исходного
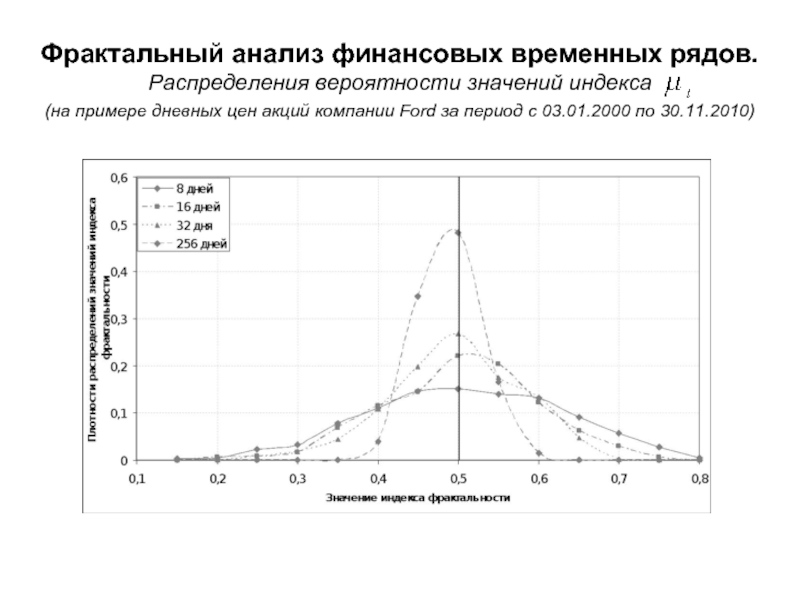
ряда 4096 дней:Слайд 33Фрактальный анализ финансовых временных рядов. Распределения вероятности значений индекса (на примере
дневных цен акций компании Ford за период с 03.01.2000 по
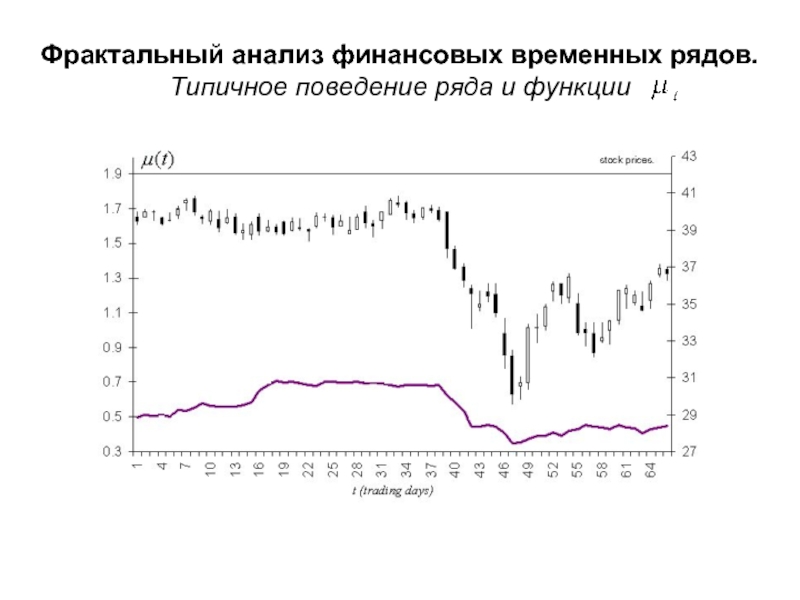
30.11.2010)Слайд 35Эффект увеличения крупномасштабных колебаний при уменьшении мелкомасштабных
Индикатор Старченко.
Слайд 36Модели обвалов на финансовом рынке
1. Инвесторы и спекулянты. Самоорганизованная критичность
(P. Back)
2. Модели взаимодействующих агентов (D. Sornette, J-P. Bouchaud, T.
Lux)K>0
Слайд 44Minority Game (Arthur W.B., Challet D., Lux T., Marsili M.,
Zhang Y-C)
Некоторые результаты:Существует функция H = f (m) , которая определяет ценность информации для получения прибыли
В игре с индуктивной динамикой существует управляющий параметр определяющий кооперативные эффекты игры
(здесь )
При этом:
- если , то (рынок не эффективен)
- если , то (рынок эффективен, симметричная фаза)
Слайд 45Другие разделы экономики:
1. Распределение богатства
(V. Yakovenko, A. Dragulescu, М.
Романовский)
2. Фирмы.(L. Amaral, S. Buldyrev, H. Stanley)
3. Влияние рекламы на
объем продаж (D. Sornette)
4. Макроэкономика и финансовая система (В.П. Маслов, В.М. Полтерович, И.Г. Поспелов, Д.С. Чернавский)
Слайд 46Эконофизика и мэйнстрим
«Лежащее в основе современной экономической теории представление о
человеке, который, исходя из рациональной оценки существующих возможностей, руководствуется лишь
собственной выгодой, на самом деле является результатом достаточно позднего установления.К счастью так было не всегда. Например, в позднем Средневековье представление о «справедливых ценах» доминировало в экономическом мышлении. Уровень цен, который устанавливался гильдиями, городским управлением и государственными контролерами, обеспечивал приемлемую прибыль для торговцев и в то же время позволял покупателям удовлетворять свои потребности без сверхзатрат. Купцы сознавали, что они должны руководствоваться не только стремлением к прибыли, но и какими-то социальными обязательствами по отношению к окружающим…
Слайд 47Эконофизика и мэйнстрим
… Но в Новое Время ситуация изменилась. Бурное
развитие международной торговли вывело экономику из-под контроля отдельных правительств и
государств. В большинстве крупных европейских городов расцвели международные торговые рынки, вследствие чего регулирование цен пришло в упадок, а купцы получили возможность продавать товары по максимальным ценам, которые могли снести покупатели. Неудивительно, что в такой обстановке очень быстро возникли и развились сугубо эгоистические формы общения. Такая система торговли нуждалась лишь в объяснении механизма своего действия, что и сделал Адам Смит, создав экономическую теорию, объясняющую и фактически оправдывающую возникшую систему».Philip Ball: CRITICAL MASS
Слайд 49Литература:
1. Мантенья Р.Н., Стенли Г.Ю. Введение в эконофизику. URSS. М.:
2009
2. Сорнетте Дидье. Как предсказывать крахи финансовых рынков. Критические события
в комплексных финансовых системах. М.: Интернет-Трейдинг, 20033. Романорвский М.Ю., Романовский Ю.М. Введение в эконофизику. М.: 2007
4. Bouchaud J.-P., Potters M. Theory of Financial Risks: From Statistical Physics to Risk Management. Cambridge, New York, Cambridge University Press, 2000
5. Dubovikov M.M., Starchenko N.S., Dubovikov M.S. Dimension of the minimal cover and fractal analysis of time series // Physica. 2004. A 339. Р. 591 – 608
6. Ball Ph. Critical mass. Farrar, Straus and Giroux, New York, 2004
7. Mantegna R.N., Stanley H.E. Scaling behavior in the dynamics of an economic index // Nature. 1995. 376. Р. 46 – 49
8. Gabaix X., Gopikrishnan P., Plerou V., Stanley H.E. A theory of power-law distri-butions in financial market fluctuations // Nature. 2003. 423. Р. 267 – 270
9. Bak Per, Paczuski, M. Shubik, Price Variations in a Stock Market with Many Agents, Working paper 96-05-078, Santa Fe Institute Economics Research Pro-gramm, 1996
10.Challet D., Chessa A., Marsili M., Zhang Y-C. From minority games to real mar-kets // Quantitative Finance. 2001. 1(1). Р. 168 – 176
Теги
















![Основные направления эконофизики. Фрактальный анализ финансовых рядов ФракталыФинансовые временные ряды Размерность минимального покрытия Индекс фрактальности Для функции f(t), ФракталыФинансовые временные ряды Размерность минимального покрытия Индекс фрактальности Для функции f(t), определенной на [a,b] введем](/img/thumbs/0c2b20ecb4db2e0b368d39c5c9b27cc0-800x.jpg)