Процесс многократного рассеяния

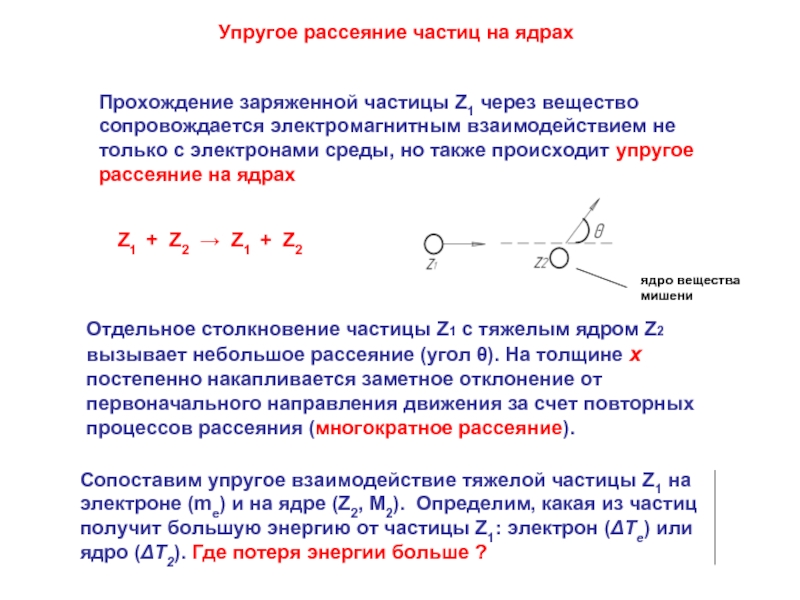
электроне и на ядре
Процесс многократного рассеяния в слое вещества
Оценка

«Процесс многократного рассеяния»

Z2
Отдельное столкновение частицы Z1 с тяжелым ядром Z2 вызывает небольшое

Сопоставим упругое взаимодействие тяжелой частицы Z1 на электроне (me) и на ядре (Z2, M2). Определим, какая из частиц получит большую энергию от частицы Z1: электрон (ΔΤе) или ядро (ΔΤ2). Где потеря энергии больше ?

Прохождение заряженной частицы Z1 через вещество сопровождается электромагнитным взаимодействием не только с электронами среды, но также происходит упругое рассеяние на ядрах

ядро вещества мишени

упругое взаимодействие тяжелой частицы Z1 на электроне (me) и на

частица Z1 пролетает мимо электрона и ядра с одинаковым прицельным параметром ρ и с одинаковой скоростью V1

не должна заметно терять энергию: T1(x =0) ≈ T1(x). Импульс

Суммарный угол θ =Σ θi, где θi – рассеяние в i-ом взаимодействии, не может служить мерой рассеяния. Его величина, с учетом знака углов отклонений θi, равна нулю.

Принято оценивать квадратичный угол: = Σ θi2

Для учета взаимодействия частицы Z1 с отдельным ядром i можно использовать формулу Резерфорда

Условия расчета:

ядром


Расчет в приближении малых углов - в расчетах взято

Значения предельных углов связаны с размерами ядра (Rяд) и атома (Rат) и зависят от материала вещества-мишени

как сумма значений по полному числу отдельных i независимых столкновений

m = σ·n·x

σ(см2) – полное резерфордовское сечение рассеяния
n(1/cм3) – концентрация ядер мишени
Х (см) – толщина мишени

Получается функциональная зависимость вида:

Заряженная частица (Z1), движущаяся с импульсом р1
(скорость v1) через вещество толщиной х,
приобретает среднеквадратичный угол

Точные расчеты дают подобную зависимость:

L - длина взаимодействия

р1, попадает в однородное магнитное поле перпендикулярно вектору Н.
Частица

Их равенство позволяет вычислить
величину радиуса вращения в магнитном поле

Эта запись справедлива и для релятивистского случая

Получаем:

спектрометр (заполненный веществом) и проходит расстояние d перпендикулярно направлению поля

На толщине спектрометра d отношение угла многократного рассеяния к углу поворота в магнитном поле запишется в виде

Скорость частицы выражается через импульс

При определенных сочетаниях параметров частицы, поля и характеристик среды искажающее влияние многократного рассеяния может быть минимизировано.