Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Самостоятельная работа по физике
Содержание
- 1. Самостоятельная работа по физике
- 2. Параллелельный колебательный контурЛитератураВ.П. Попов, 1998 г. –
- 3. При Входные ЧХ = ==ρ
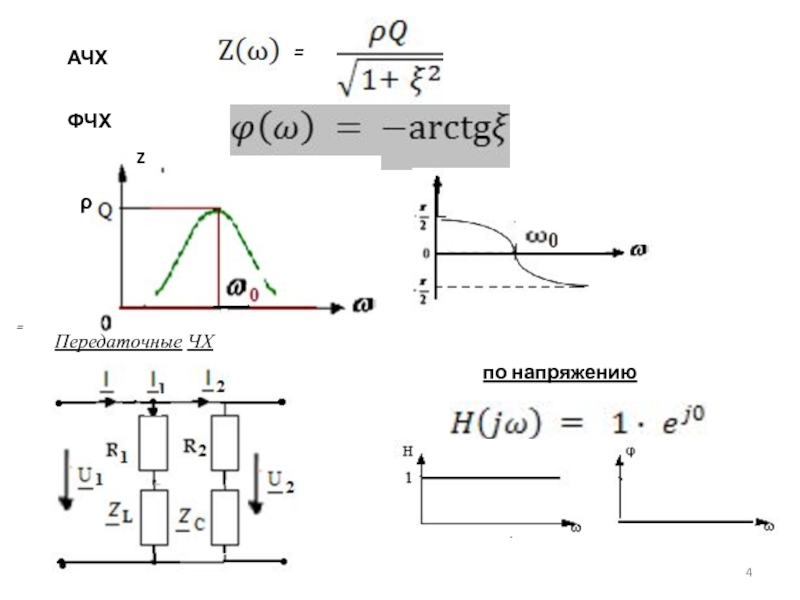
- 4. АЧХ = = ФЧХρZПередаточные ЧХпо напряжению
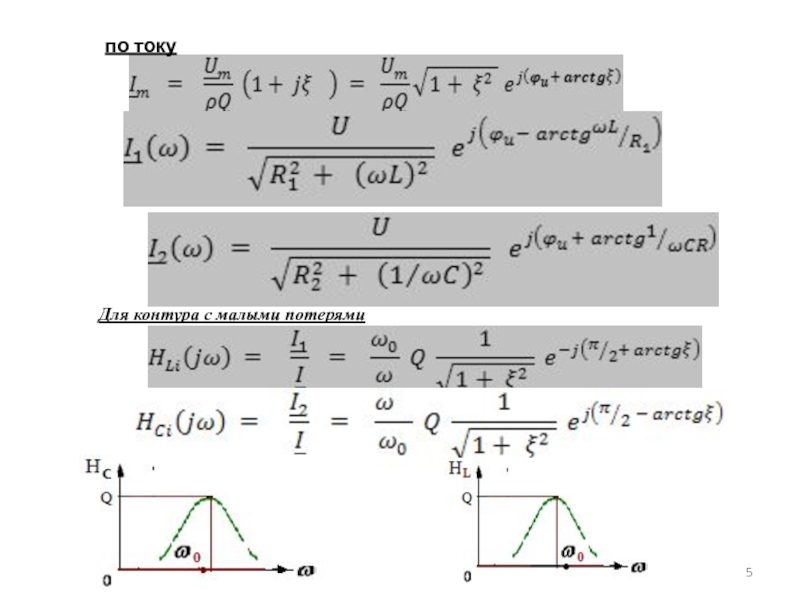
- 5. по токуДля контура с малыми потерями
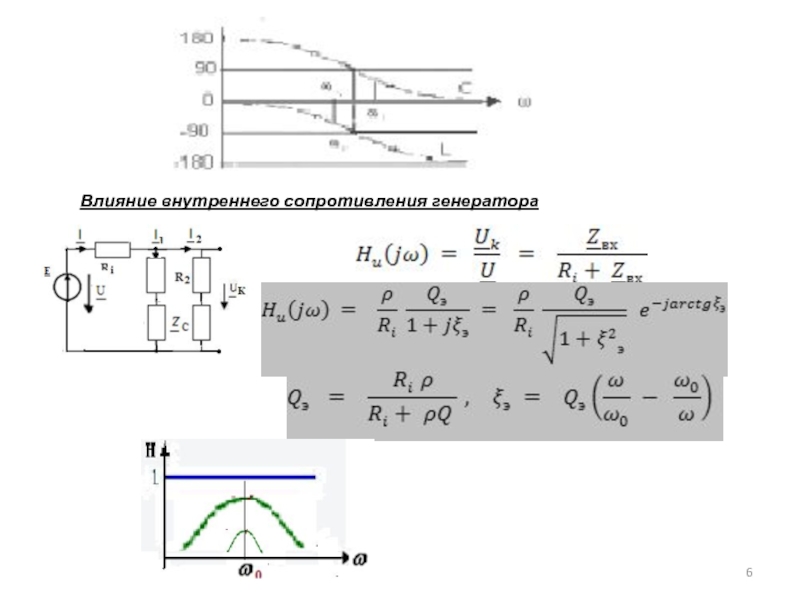
- 6. Влияние внутреннего сопротивления генератора
- 7. Частотные характеристики связанных контуровДва контура называются связанными,
- 8. Комплексные схемы замещенияКоэффициент связитрансформаторная связь - внутренняя индуктивной связь -внутренняя ёмкостная связь -12
- 9. Схема замещения 1Обозначения
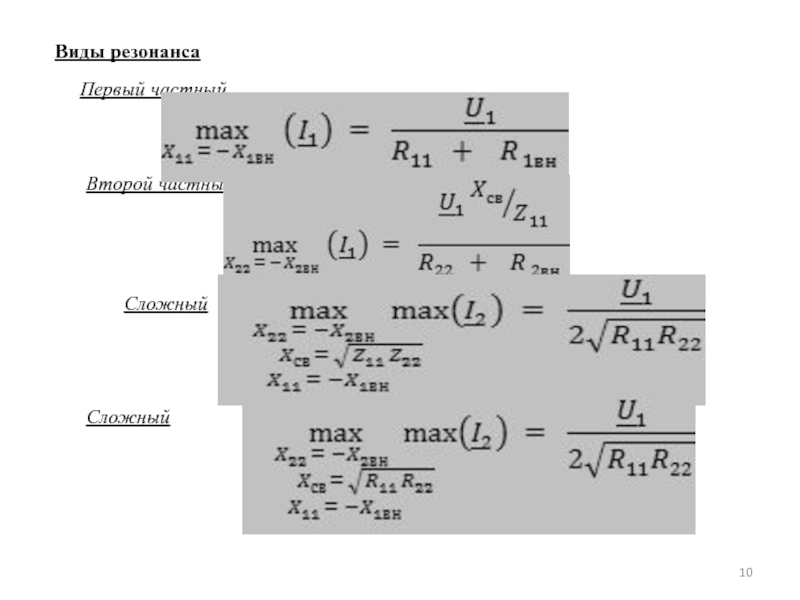
- 10. Виды резонансаПервый частныйВторой частныйСложныйСложный
- 11. При Zсв = jXсвНормированная
- 12. Слайд 12
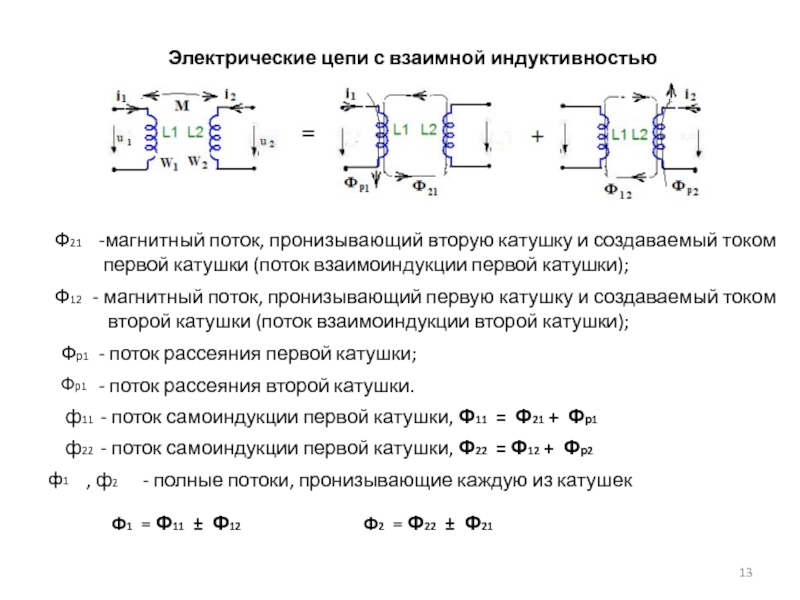
- 13. Электрические цепи с взаимной индуктивностьюФ21 -магнитный поток,
- 14. Ψ = wФ = L
- 15. Одноимённые зажимыОдноимёнными называются такие зажимы магнитно связанных
- 16. Анализ электрических цепей с взаимной индуктивностьюКомпонентные уравнения
- 17. Эквивалентные преобразования цепей со связанными индуктивностямиПоследовательное включениеПараллельное включениеРазвязка магнитных цепей
- 18. Эквивалентные преобразования цепей со связанными индуктивностямиПоследовательное включениеПараллельное включениеРазвязка магнитных цепейЛитератураВ.П. Попов, 1998 г. – с. 142-154
- 19. Скачать презентанцию
Параллелельный колебательный контурЛитератураВ.П. Попов, 1998 г. – с. 198-223А.Ф. Белецкий, 1986 г. – с. 156-176В.П. Бакалов и др., 2000 г. – с.121-134
Слайды и текст этой презентации
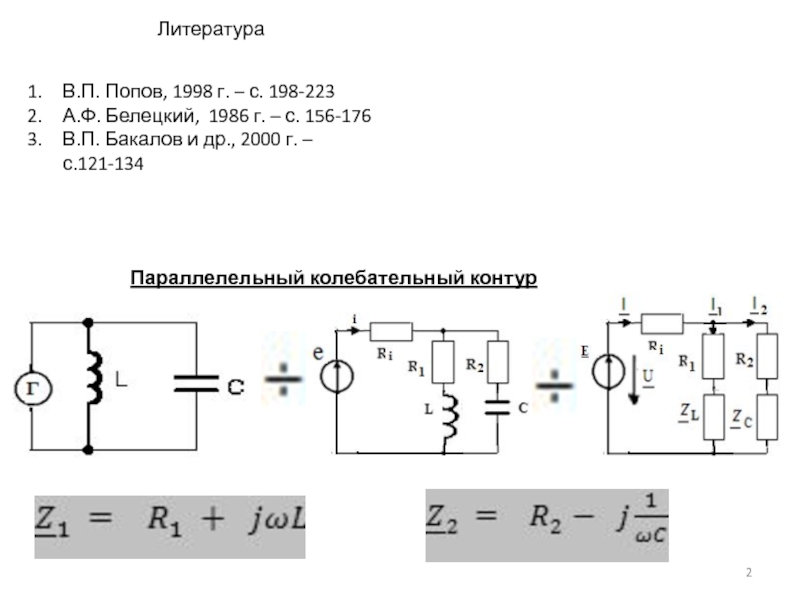
Слайд 2Параллелельный колебательный контур
Литература
В.П. Попов, 1998 г. – с. 198-223
А.Ф. Белецкий,
1986 г. – с. 156-176
– с.121-134
Слайд 7Частотные характеристики связанных контуров
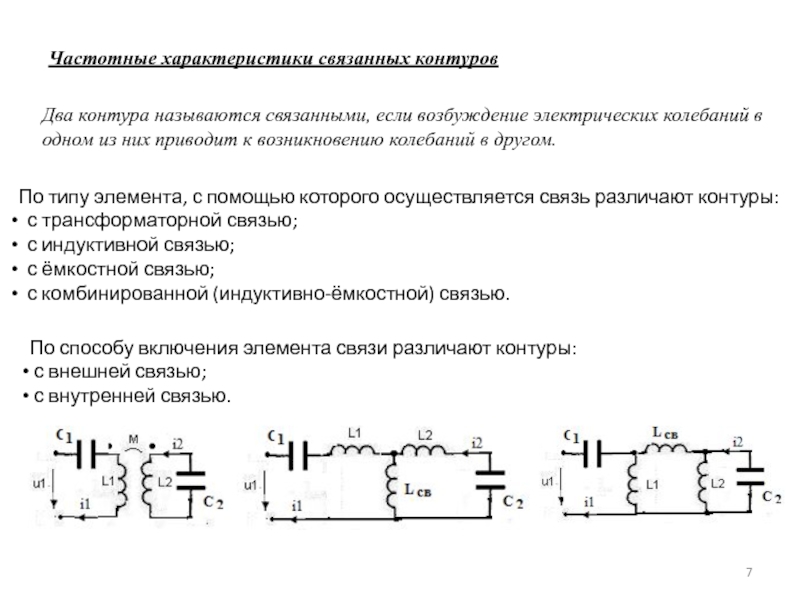
Два контура называются связанными, если возбуждение электрических
колебаний в одном из них приводит к возникновению колебаний в
другом.По типу элемента, с помощью которого осуществляется связь различают контуры:
с трансформаторной связью;
с индуктивной связью;
с ёмкостной связью;
с комбинированной (индуктивно-ёмкостной) связью.
По способу включения элемента связи различают контуры:
с внешней связью;
с внутренней связью.
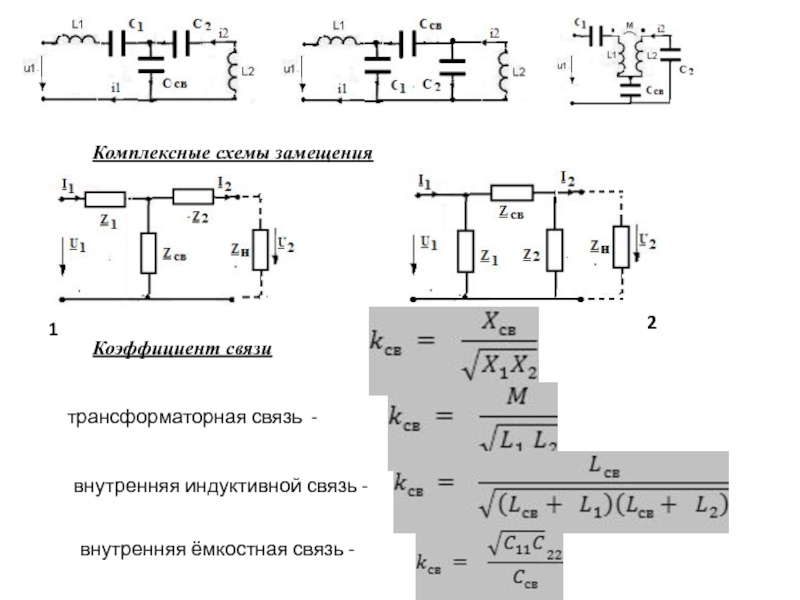
Слайд 8Комплексные схемы замещения
Коэффициент связи
трансформаторная связь -
внутренняя индуктивной связь
-
внутренняя ёмкостная связь -
1
2
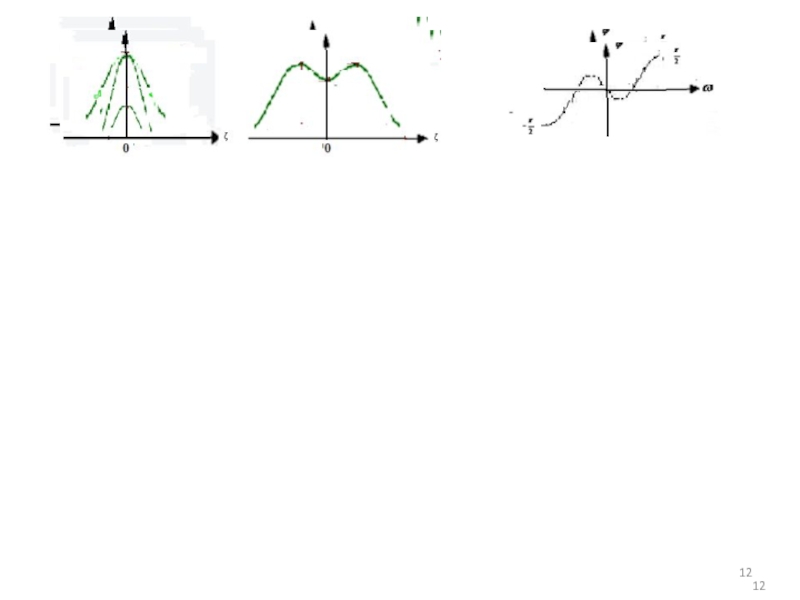
Слайд 11При Zсв = jXсв
Нормированная относительно
A –
фактор связи
АЧХ тока I2
K < d,
( A < 1) - слабая связьK > d, ( A > 1) - сильная связь
K = d, ( A = 1) - критическая связь
Слайд 13Электрические цепи с взаимной индуктивностью
Ф21
-магнитный поток, пронизывающий вторую катушку
и создаваемый током
первой катушки (поток взаимоиндукции первой катушки);
Ф12
магнитный
поток, пронизывающий первую катушку и создаваемый токомвторой катушки (поток взаимоиндукции второй катушки);
Фр1
- поток рассеяния первой катушки;
- поток рассеяния второй катушки.
Фр1
ф11 - поток самоиндукции первой катушки, Ф11 = Ф21 + Фр1
ф22 - поток самоиндукции первой катушки, Ф22 = Ф12 + Фр2
- полные потоки, пронизывающие каждую из катушек
ф1
, ф2
Ф1 = Ф11 ± Ф12
Ф2 = Ф22 ± Ф21
Слайд 14Ψ = wФ = L i
ЭДС, наводимые в
связанных катушках
L2 = Ψ 22 ⁄ i2
М12 = Ψ
12 ⁄ i2 = - dΨ ⁄ dt = -
М21 = Ψ 21 ⁄ i1
Ψ ij
= wi Фij
Закон электромагнитной индукции
e
L1 = Ψ 11 ⁄ i1
(dΨ ⁄ di)(di ⁄ dt)
Напряжения на зажимах катушек
Слайд 15Одноимённые зажимы
Одноимёнными называются такие зажимы магнитно связанных элементов, когда
при одинаковом
направлении токов относительно этих зажимов (оба тока «входят»,
или оба тока
«выходят» со стороны этих зажимов) магнитные потоки обоих элементов направлены согласно
Коэффициент магнитной связи
Слайд 16Анализ электрических цепей с взаимной индуктивностью
Компонентные уравнения для связанных индуктивностей
в комплексной форме
Система уравнений электрического равновесия
(0)
(1)
Слайд 17Эквивалентные преобразования цепей со связанными индуктивностями
Последовательное включение
Параллельное включение
Развязка магнитных цепей
Слайд 18Эквивалентные преобразования цепей со связанными индуктивностями
Последовательное включение
Параллельное включение
Развязка магнитных цепей
Литература
В.П.
Попов, 1998 г. – с. 142-154
