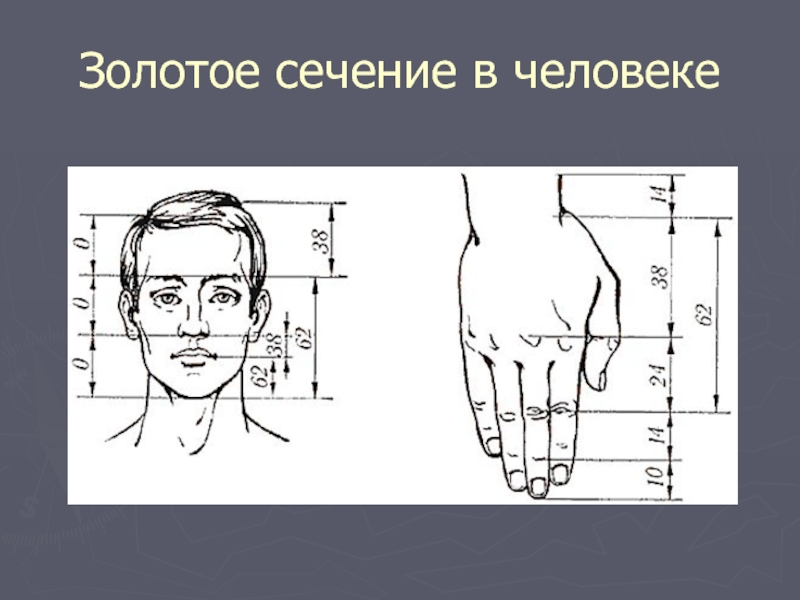
Слайд 2Золотое сечение
Если разделить любой отрезок на две части так, чтобы
отношение большей части отрезка к целому было равно отношению меньшей
части к большей, получим сечение, которое называют золотым.
На рисунке отрезок АВ разделен точкой С так, что АС : АВ = СВ : АС. Отношение большей части отрезка к меньшей и всей длины отрезка к большей его части (Ф) равно приблизительно 1,618... Обратная величина - отношение меньшей части отрезка к большей и большей части к всему отрезку - составляет примерно 0,618...
Нетрудно заметить, что взаимно обратные величины 0,618... и 1,618... отличаются только первой цифрой. Эти числа получили название «золотых» чисел
Слайд 3Золотое сечение
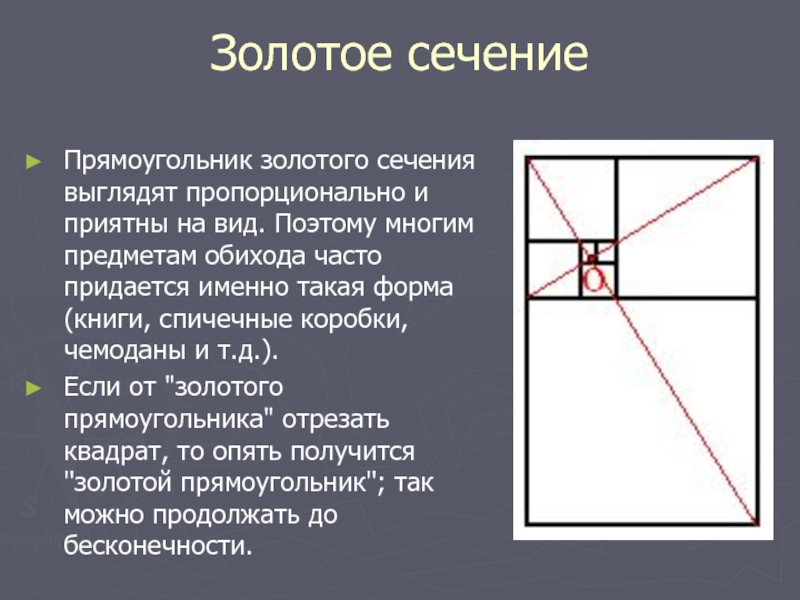
Прямоугольник золотого сечения выглядят пропорционально и приятны на вид.
Поэтому многим предметам обихода часто придается именно такая форма (книги,
спичечные коробки, чемоданы и т.д.).
Если от "золотого прямоугольника" отрезать квадрат, то опять получится "золотой прямоугольник"; так можно продолжать до бесконечности.
Слайд 4Золотое сечение
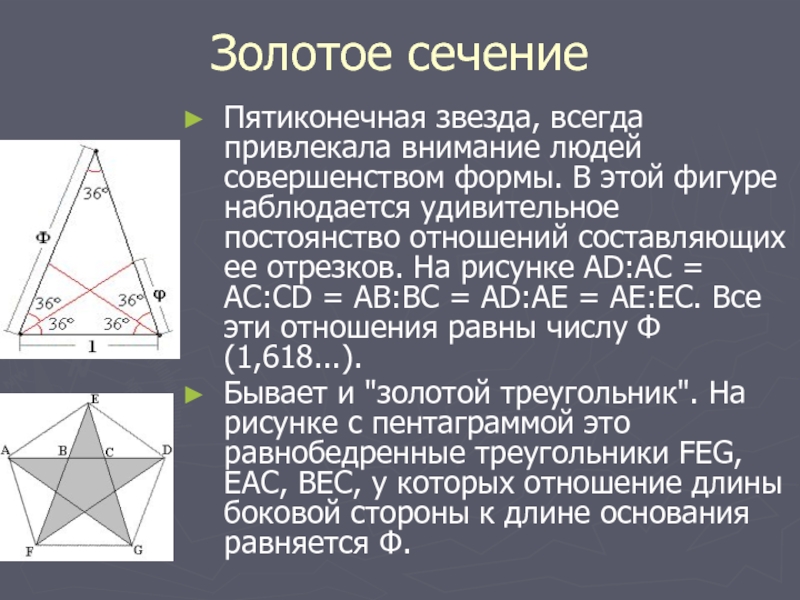
Пятиконечная звезда, всегда привлекала внимание людей совершенством формы. В
этой фигуре наблюдается удивительное постоянство отношений составляющих ее отрезков. На
рисунке AD:AC = AC:CD = AB:BC = AD:AE = AE:EC. Все эти отношения равны числу Ф (1,618...).
Бывает и "золотой треугольник". На рисунке с пентаграммой это равнобедренные треугольники FEG, EAC, BEC, у которых отношение длины боковой стороны к длине основания равняется Ф.
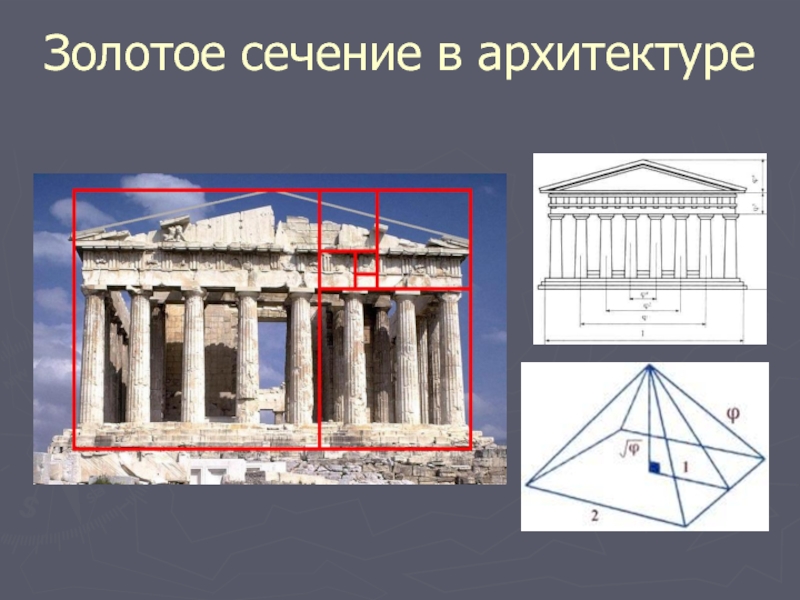
Слайд 5Золотое сечение в архитектуре
Слайд 9Числа Фибоначчи
Леонардо Пизанский
(Фибоначчи – сын
Боначчи)
1180 – 1240гг.
Слайд 10Числа Фибоначчи
Задача, помещенная на странице 123-124 рукописи 1228 года: «Сколько
пар кроликов в один год от одной пары рождается?», имеет
следующее решение по месяцам:
1,1,2,3,5,8,13,21,34,55,89,144,233,377…
В честь автора этой задачи вся последовательность называется числами Фибоначчи.
Слайд 16Число Пи
(произносится «пи») — математическая константа, выражающая отношение длины окружности к
длине её диаметра. Обозначается буквой греческого алфавита «пи».
если принять
диаметр окружности за единицу, то длина окружности — это число «пи».
Слайд 17Число Пи
510 знаков после запятой:
π ≈ 3,141 592 653
589 793 238 462 643 383 279 502 884 197
169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 067 982 148 086 513 282 306 647 093 844 609 550 582 231 725 359 408 128 481 117 450 284 102 701 938 521 105 559 644 622 948 954 930 381 964 428 810 975 665 933 446 128 475 648 233 786 783 165 271 201 909 145 648 566 923 460 348 610 454 326 648 213 393 607 260 249 141 273 724 587 006 606 315 588 174 881 520 920 962 829 254 091 715 364 367 892 590 360 011 330 530 548 820 466 521 384 146 951 941 511 609 433 057 270 365 759 591 953 092 186 117 381 932 611 793 105 118 548 074 462 379 962 749 567 351 885 752 724 891 227 938 183 011 949 129 833 673 362…
Слайд 18Число Пи
Памятник числу «пи» на ступенях перед зданием Музея искусств
в Сиэтле.
Неофициальный праздник «День числа пи» отмечается 14 марта, которое
в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа π.
Ещё одной датой, связанной с числом π, является 22 июля, которое называется «Днём приближённого числа Пи» , так как в европейском формате дат этот день записывается как 22/7, а значение этой дроби является приближённым значением числа πи.