Слайд 1ПОВОРОТ
Пусть теперь в пространстве задана прямая a
и точка A, не принадлежащая этой прямой. Через точку A
проведем плоскость α, перпендикулярную прямой a, и точку пересечения a и α обозначим O. Говорят, что точка A' пространства получается из точки A поворотом вокруг прямой a на угол φ, если в плоскости α точка A' получается из точки A поворотом вокруг центра O на угол φ.
Преобразование пространства, при котором точки прямой a остаются на месте, а все остальные точки поворачиваются вокруг этой прямой (в одном и том же направлении) на угол φ называется поворотом, или вращением. Прямая a при этом называется осью вращения.
Слайд 2ФИГУРЫ ВРАЩЕНИЯ
Говорят,что фигура Ф в пространстве получена
вращением фигуры F вокруг оси a, если точки фигуры Ф
получаются всевозможными поворотами точек фигуры F вокруг оси a. Фигура Ф при этом называется фигурой вращения.
При вращении точки A вокруг прямой a получается окружность.
Сфера получается вращением окружности вокруг ее диаметра. Аналогично, шар получается вращением круга вокруг какого-нибудь его диаметра.
Слайд 3ФИГУРЫ ВРАЩЕНИЯ
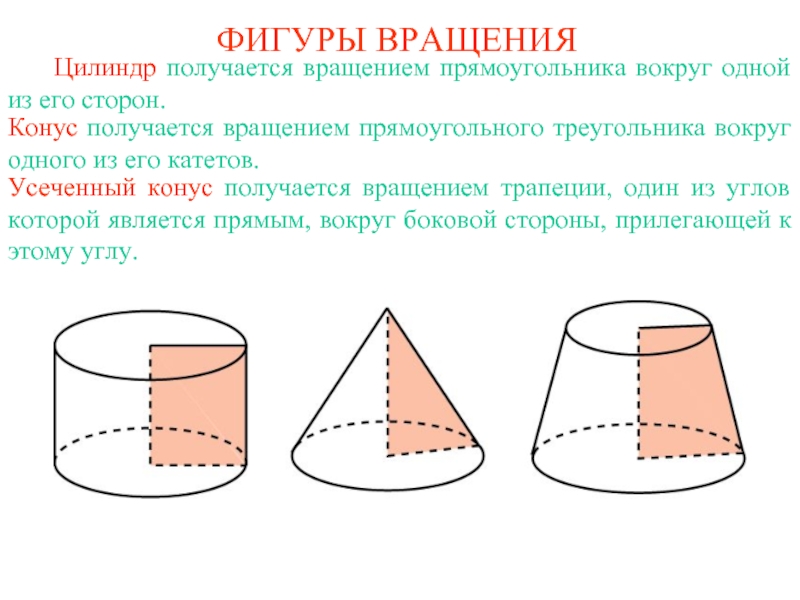
Цилиндр получается вращением прямоугольника вокруг одной
из его сторон.
Конус получается вращением прямоугольного треугольника вокруг одного
из его катетов.
Усеченный конус получается вращением трапеции, один из углов которой является прямым, вокруг боковой стороны, прилегающей к этому углу.
Слайд 4ФИГУРЫ ВРАЩЕНИЯ
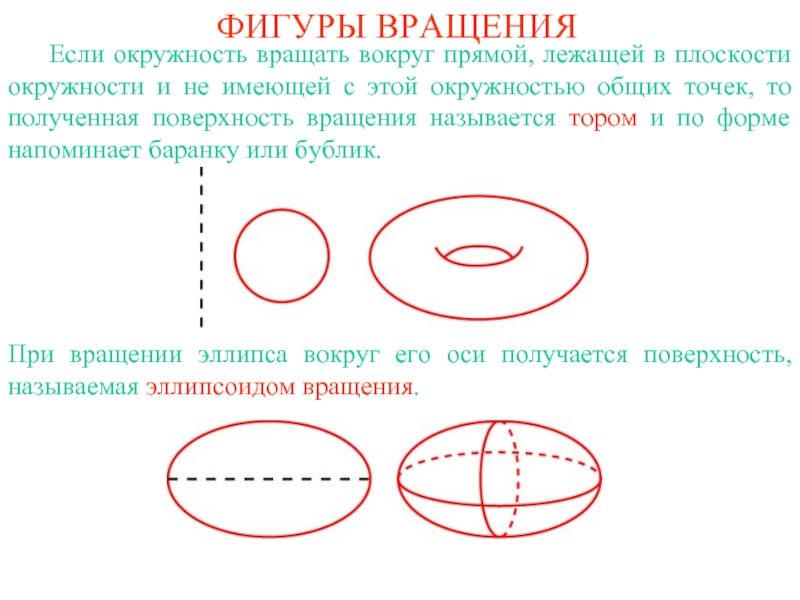
Если окружность вращать вокруг прямой, лежащей
в плоскости окружности и не имеющей с этой окружностью общих
точек, то полученная поверхность вращения называется тором и по форме напоминает баранку или бублик.
При вращении эллипса вокруг его оси получается поверхность, называемая эллипсоидом вращения.
Слайд 5ФИГУРЫ ВРАЩЕНИЯ
При вращении параболы вокруг ее оси
получается поверхность, называемая параболоидом вращения.
При вращении гиперболы вокруг ее оси
получается поверхность, называемая гиперболоидом вращения.
Слайд 6ФИГУРЫ ВРАЩЕНИЯ
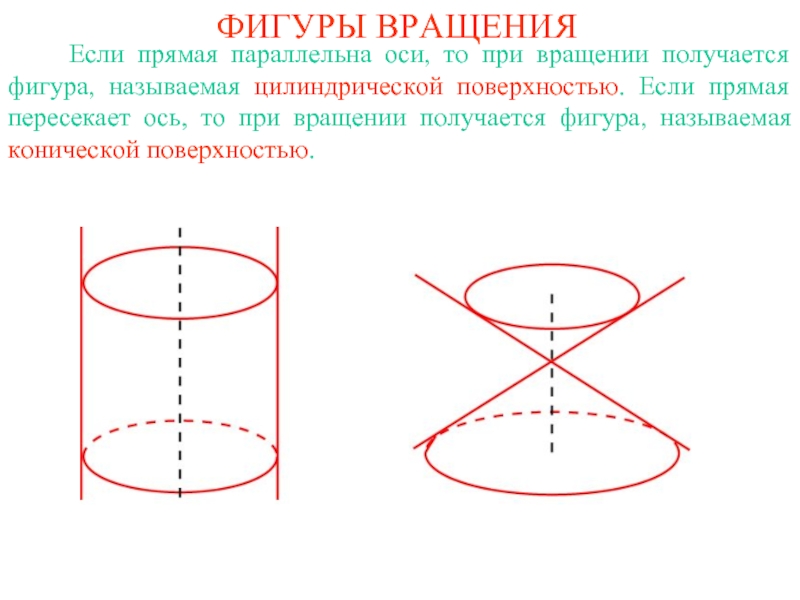
Если прямая параллельна оси, то при
вращении получается фигура, называемая цилиндрической поверхностью. Если прямая пересекает ось,
то при вращении получается фигура, называемая конической поверхностью.
Слайд 7ГИПЕРБОЛОИД ВРАЩЕНИЯ
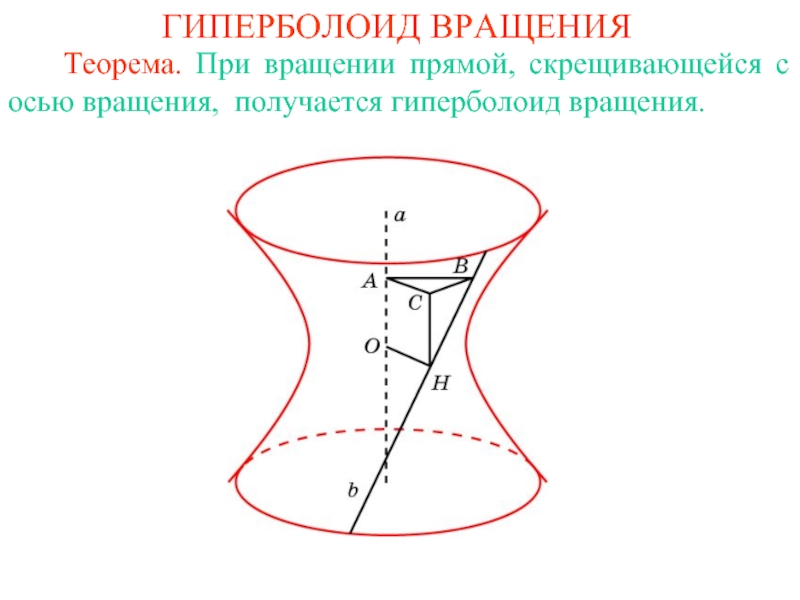
Теорема. При вращении прямой, скрещивающейся с
осью вращения, получается гиперболоид вращения.
Слайд 8ВРАЩЕНИЕ КУБА 1
При вращении куба вокруг диагонали
получается фигура, поверхность которой состоит из боковых поверхностей двух конусов
и поверхности гиперболоида вращения.
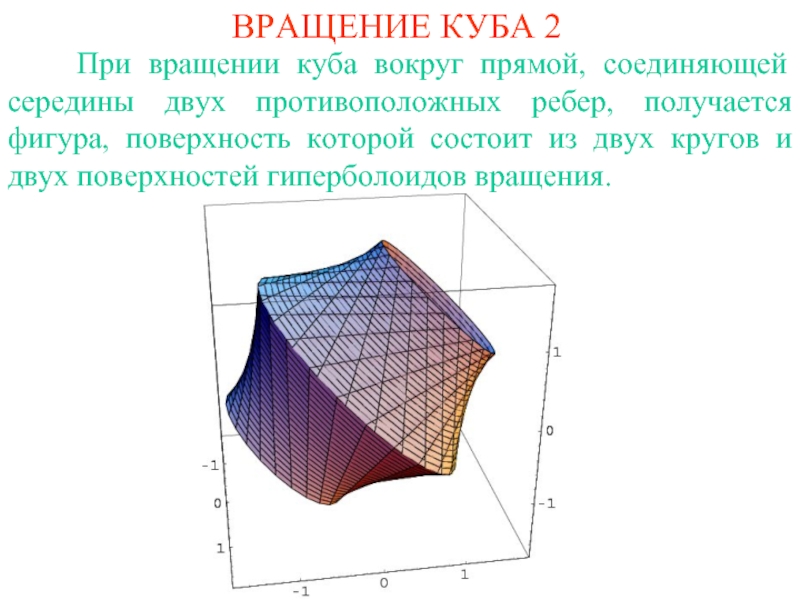
Слайд 9ВРАЩЕНИЕ КУБА 2
При вращении куба вокруг прямой,
соединяющей середины двух противоположных ребер, получается фигура, поверхность которой состоит
из двух кругов и двух поверхностей гиперболоидов вращения.
Слайд 10Упражнение 1
Какая фигура получается при вращении отрезка OA вокруг прямой,
проходящей через точку O и перпендикулярной OA?
Ответ: Круг.
Слайд 11Упражнение 2
Назовите прямые, при вращении вокруг которых данного прямоугольника получается
цилиндр.
Ответ: Прямые, пересекающие прямоугольник по отрезку, параллельному его стороне.
Слайд 12Упражнение 3
Какая фигура получается при вращении равнобедренного треугольника вокруг прямой,
содержащей высоту, опущенной на основание этого треугольника?
Ответ: Конус.
Слайд 13Упражнение 4
Какая фигура получается при вращении полукруга вокруг прямой, содержащей
диаметр?
Ответ: Круг.
Слайд 14Упражнение 5
Какая фигура получается вращением прямоугольного треугольника вокруг прямой, содержащей
его катет?
Ответ: Конус.
Слайд 15Упражнение 6
Какая фигура получается вращением прямоугольного треугольника вокруг прямой, лежащей
в плоскости этого треугольника, и проходящей через вершину острого угла
перпендикулярно катету?
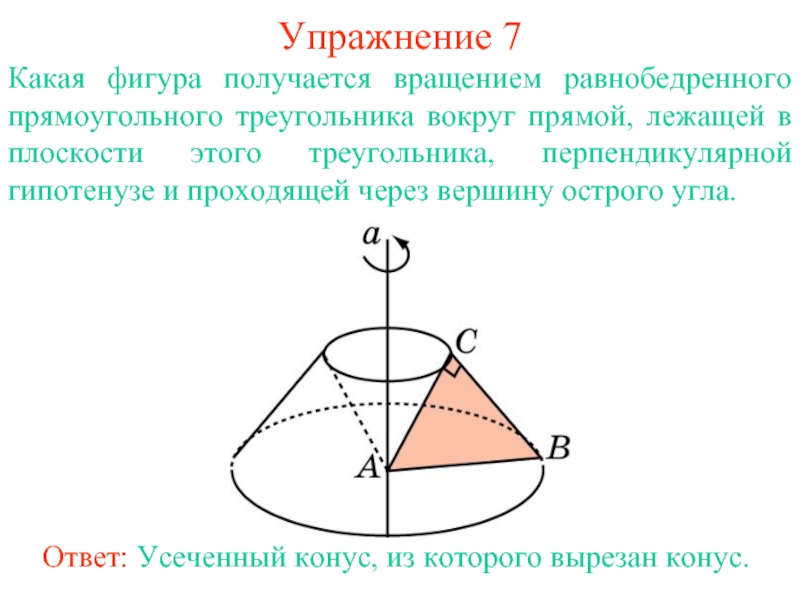
Слайд 16Упражнение 7
Какая фигура получается вращением равнобедренного прямоугольного треугольника вокруг прямой,
лежащей в плоскости этого треугольника, перпендикулярной гипотенузе и проходящей через
вершину острого угла.
Слайд 17Упражнение 8
Какая фигура получается вращением остроугольного треугольника вокруг прямой, содержащей
его сторону?
Ответ: Фигура, состоящая из двух конусов с общим основанием.
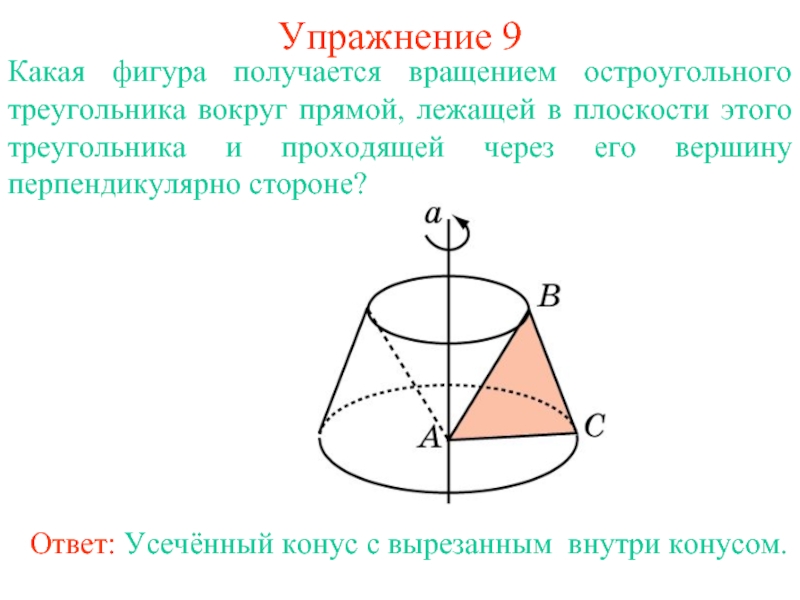
Слайд 18Упражнение 9
Какая фигура получается вращением остроугольного треугольника вокруг прямой, лежащей
в плоскости этого треугольника и проходящей через его вершину перпендикулярно
стороне?
Слайд 19Упражнение 10
Какая фигура получается вращением тупоугольного треугольника вокруг прямой, содержащей
его сторону, прилегающую к тупому углу?
Ответ: Фигура, полученная из конуса,
вырезанием из него другого конуса.
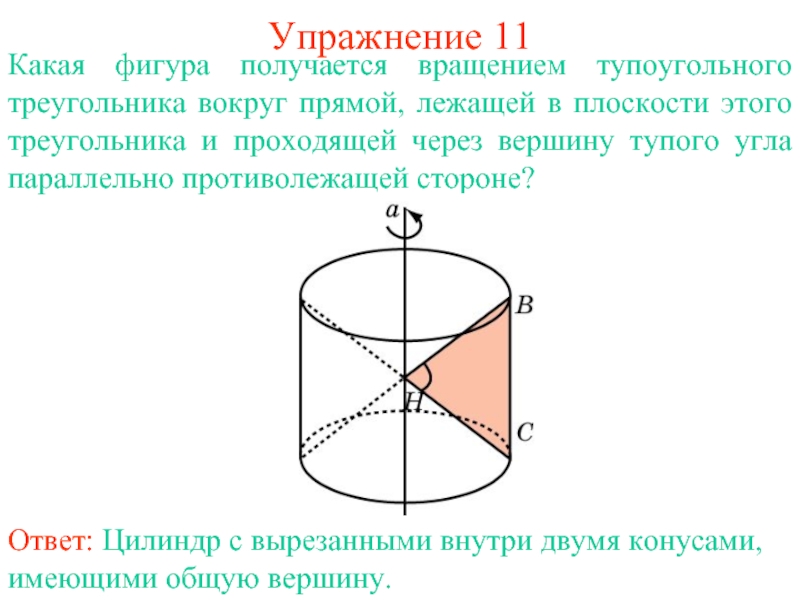
Слайд 20Упражнение 11
Какая фигура получается вращением тупоугольного треугольника вокруг прямой, лежащей
в плоскости этого треугольника и проходящей через вершину тупого угла
параллельно противолежащей стороне?
Ответ: Цилиндр с вырезанными внутри двумя конусами, имеющими общую вершину.
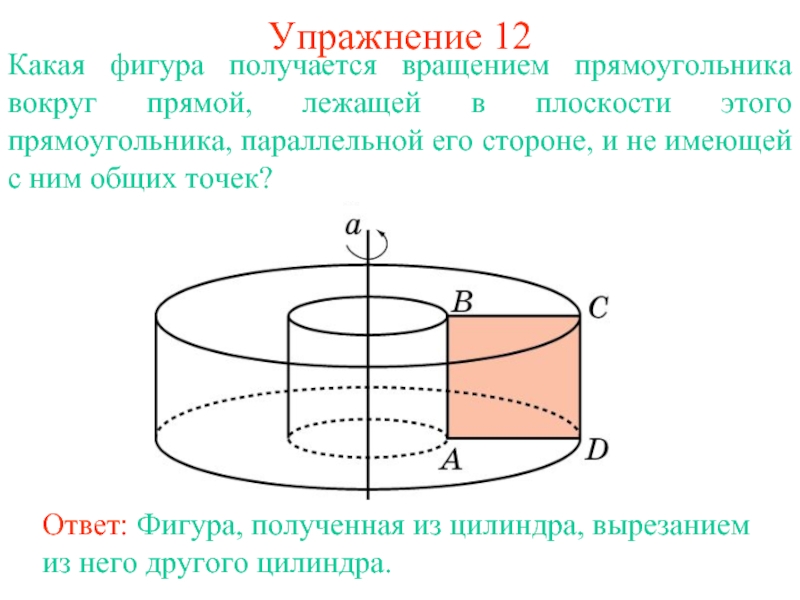
Слайд 21Упражнение 12
Какая фигура получается вращением прямоугольника вокруг прямой, лежащей в
плоскости этого прямоугольника, параллельной его стороне, и не имеющей с
ним общих точек?
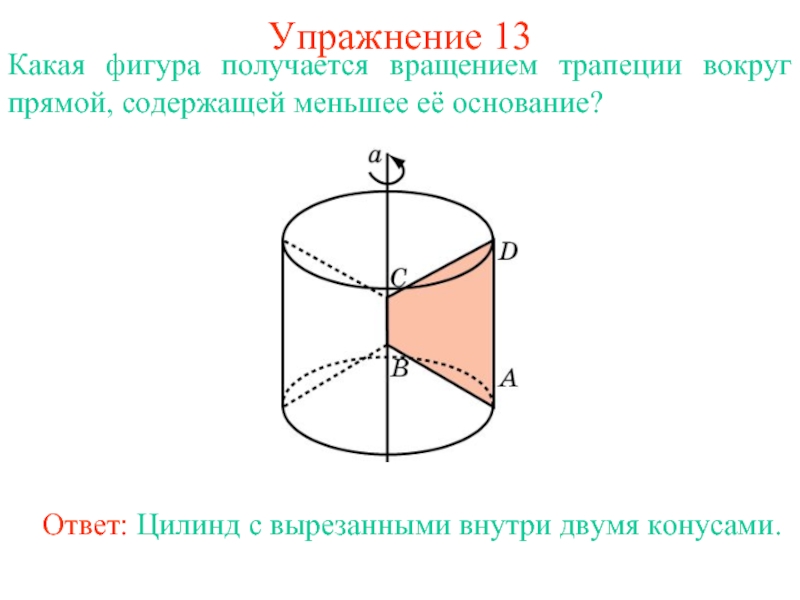
Слайд 22Упражнение 13
Какая фигура получается вращением трапеции вокруг прямой, содержащей меньшее
её основание?
Слайд 23Упражнение 14
Какая фигура получается вращением трапеции вокруг прямой, содержащей большее
её основание?
Слайд 24Упражнение 15
Какая фигура получается при вращении куба вокруг прямой, соединяющей
центры противоположных граней.
Ответ: Цилиндр.
Слайд 25Упражнение 16
Какая фигура получится при вращении правильной n-угольной призмы вокруг
прямой, проходящей через центры ее оснований?
Ответ: Цилиндр.
Слайд 26Упражнение 17
Какая фигура получается при вращении правильной n-угольной пирамиды вокруг
прямой, содержащей ее высоту?
Ответ: Конус.
Слайд 27Упражнение 18
Какая фигура получается при вращении тетраэдра вокруг прямой, соединяющей
середины скрещивающихся ребер?
Слайд 28Упражнение 19
Какая фигура получается при вращении октаэдра вокруг прямой, проходящей
через противоположные вершины?
Слайд 29Упражнение 20
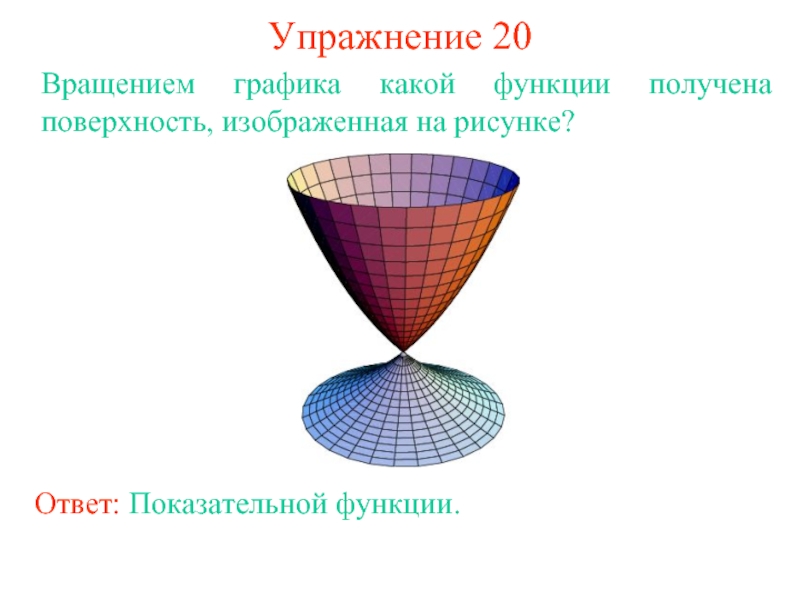
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Слайд 30Упражнение 21
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Слайд 31Упражнение 22
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Слайд 32Упражнение 23
Вращением графика какой функции получена поверхность, изображенная на рисунке?
Слайд 33Упражнение 24
Тетраэдр повернут вокруг прямой, соединяющей середины противоположных ребер, на
угол 90о. Какая фигура является объединением и пересечением исходного тетраэдра
и повернутого?
Слайд 34Упражнение 25
Куб повернут вокруг прямой, соединяющей центры противоположных граней, на
угол 45о. Какая фигура является общей частью исходного куба и
повернутого?
Слайд 35Упражнение 26
Куб повернут вокруг диагонали на угол 60о. Какая фигура
является общей частью исходного куба и повернутого?
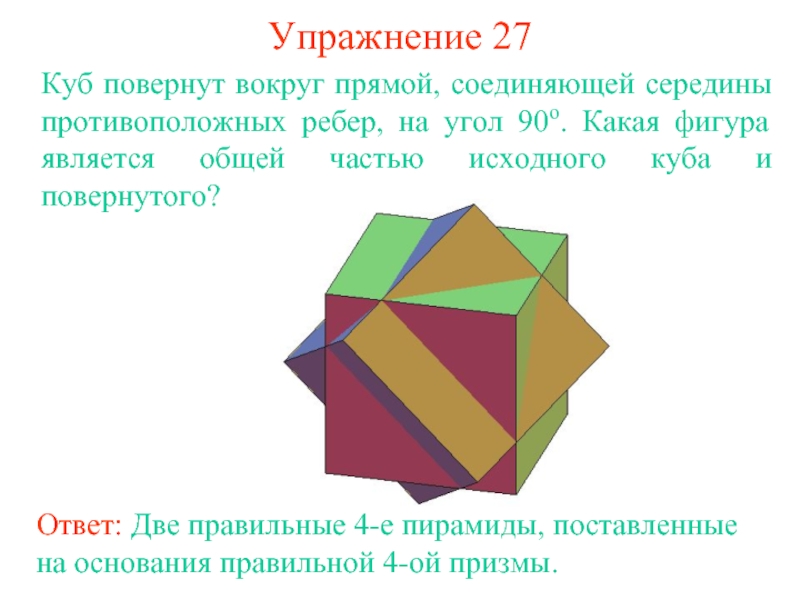
Слайд 36Упражнение 27
Куб повернут вокруг прямой, соединяющей середины противоположных ребер, на
угол 90о. Какая фигура является общей частью исходного куба и
повернутого?
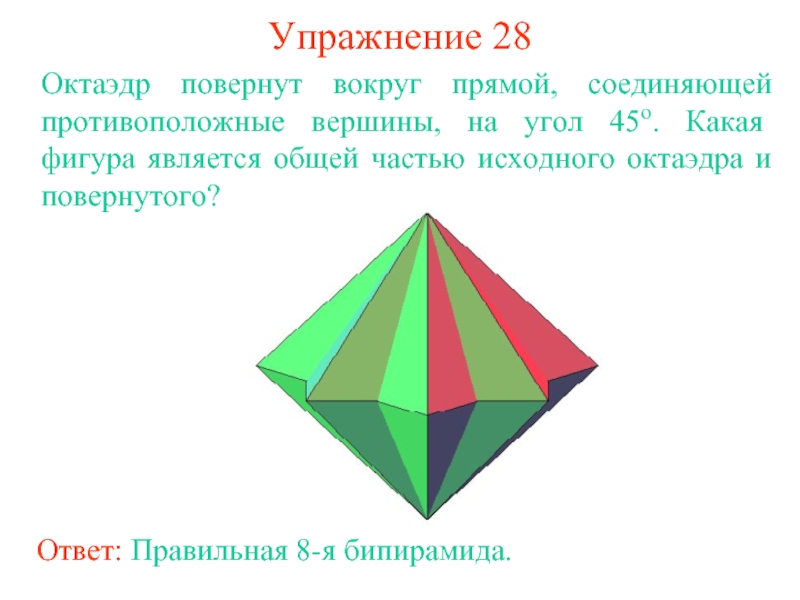
Слайд 37Упражнение 28
Октаэдр повернут вокруг прямой, соединяющей противоположные вершины, на угол
45о. Какая фигура является общей частью исходного октаэдра и повернутого?
Слайд 38Упражнение 29
Октаэдр повернут вокруг прямой, соединяющей центры противоположных граней, на
угол 60о. Какая фигура является общей частью исходного октаэдра и
повернутого?