Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Нахождение угла между скрещивающимися прямыми
Содержание
- 1. Нахождение угла между скрещивающимися прямыми
- 2. Нахождение угла между скрещивающимися прямымиДанная
- 3. Слайд 3
- 4. Задача. Все ребра
- 5. Найдем косинус B1AE1. АВ1Е1
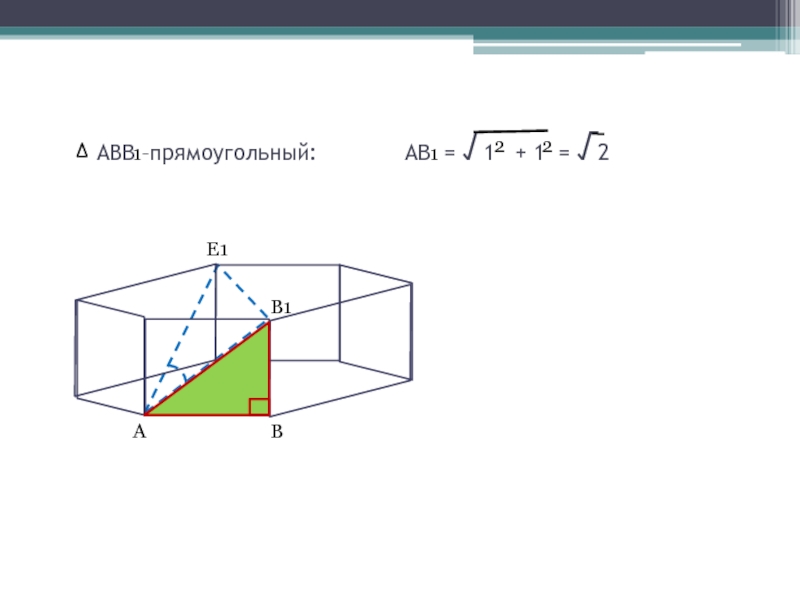
- 6. АВВ –прямоугольный:
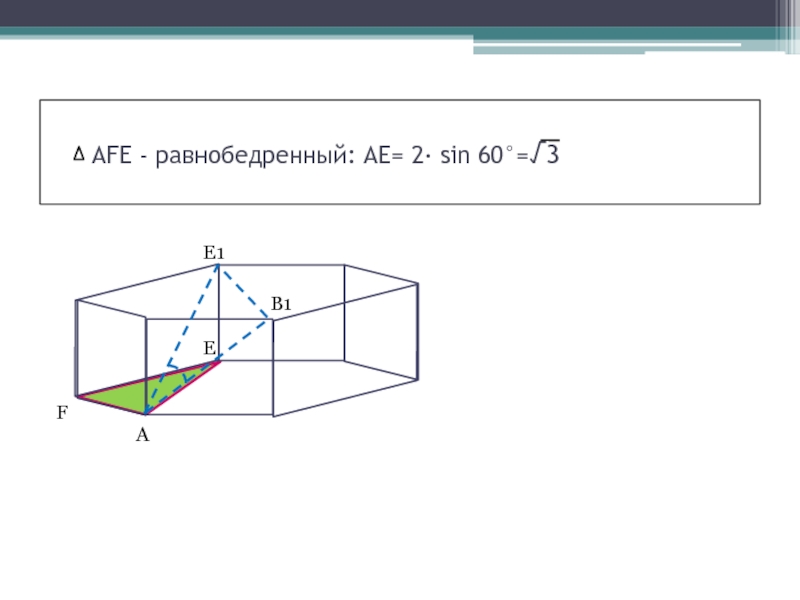
- 7. AFE - равнобедренный: АЕ= 2· sin 60°=√3 FAEE1В1
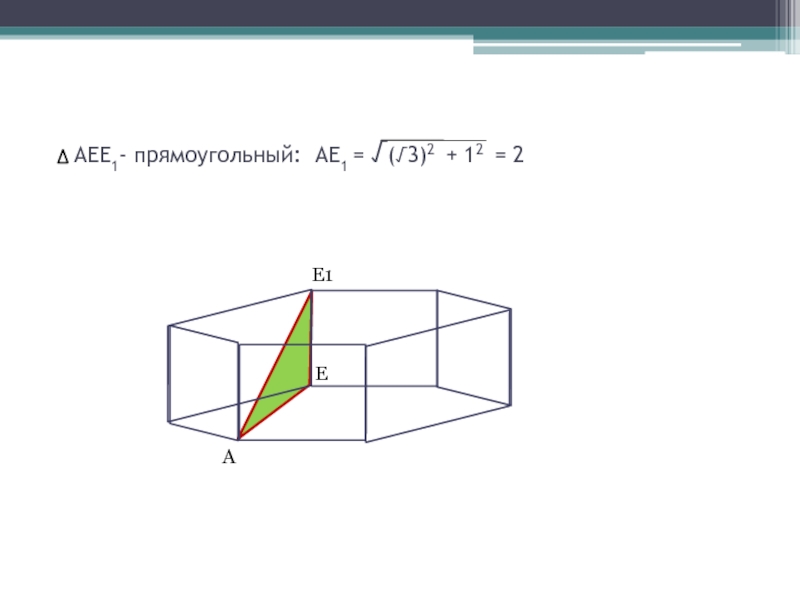
- 8. AEE1- прямоугольный: АЕ1 = √(√3)2 + 12 = 2E1AE
- 9. В1Е1= В1О1 + О1Е1 = 2,
- 10. Слайд 10
- 11. Спасибо за внимание.
- 12. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Нахождение угла между скрещивающимися прямыми.
Решение задач уровня С.
Муниципальное общеобразовательное
учреждение средняя общеобразовательная школа №85 г.о. Тольятти
Баленко Тамара БорисовнаСлайд 2
Нахождение угла между скрещивающимися прямыми
Данная тема актуальна, так как подобные
задачи требуют развитого абстрактного мышления. Задачи, представленные ниже, чаще всего
вызывают затруднения при решении у учащихся. Наглядное решение позволяет лучше усвоить приемы решения таких задач.Слайд 3
Аргументы. 1). Определение скрещивающихся прямых. 2). Определение угла между скрещивающимися прямыми. 3). Признак скрещивающихся прямых. 4). Теорема Пифагора. 5). Свойство высоты равнобедренного треугольника, проведенной к основанию. 6). Определение правильной призмы. 7). Определение синуса острого угла прямоугольного треугольника. 8). Определение косинуса острого угла прямоугольного треугольника. 9). Определение правильного многоугольника. 10). Теорема о сумме углов выпуклого многоугольника. 11). Свойство окружности, описанной около правильного шестиугольника.
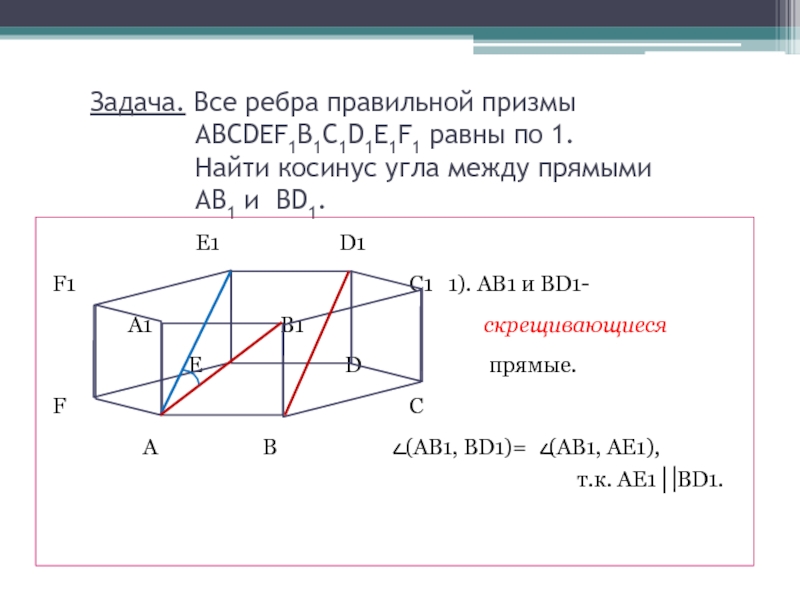
Слайд 4 Задача. Все ребра правильной призмы
ABCDEF1B1C1D1E1F1 равны по 1.
Найти косинус угла между прямыми AB1 и BD1. E1 D1
F1 C1 1). AB1 и BD1-
A1 B1 скрещивающиеся
E D прямые.
F C
A B (AB1, BD1)= (AB1, AE1),
т.к. AE1│ BD1.
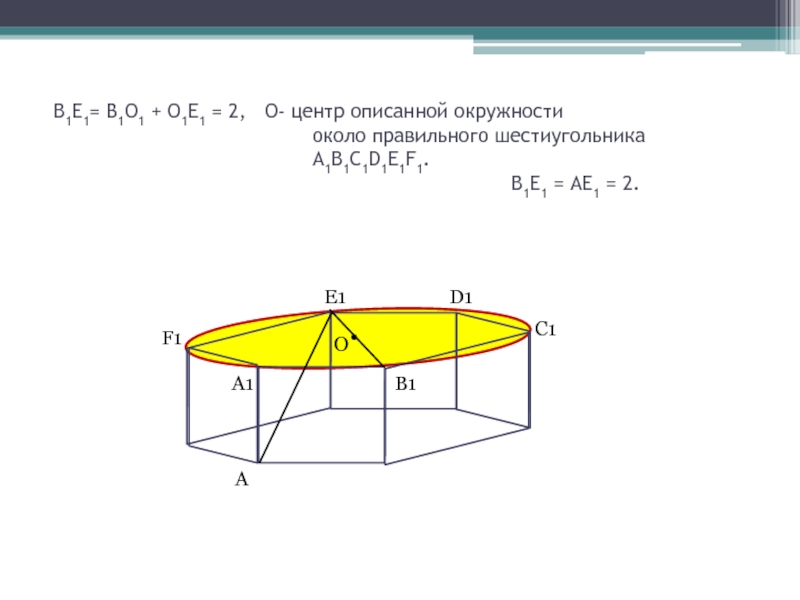
Слайд 9 В1Е1= В1О1 + О1Е1 = 2, О- центр
описанной окружности
около правильного шестиугольника A1B1C1D1E1F1. В1Е1 = АЕ1 = 2. F1
E1
D1
B1
C1
A1
O
A