Определение призмы, пирамиды

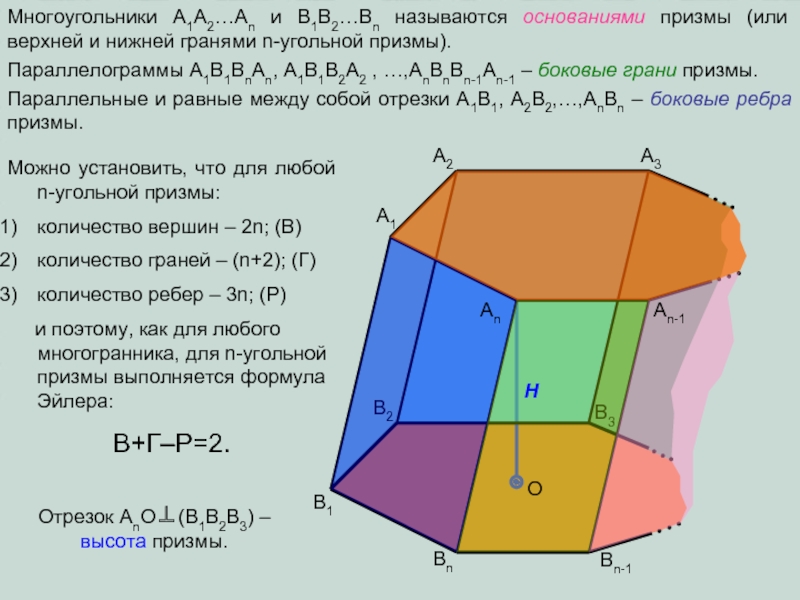
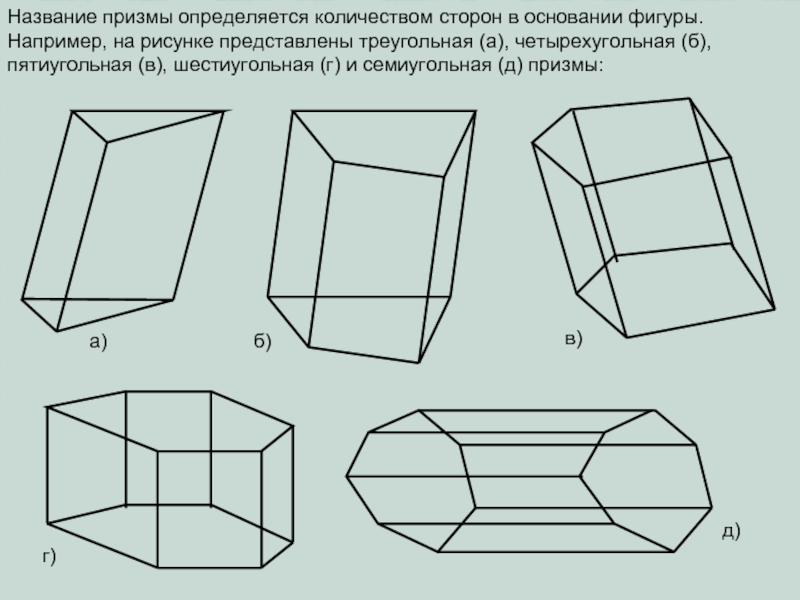
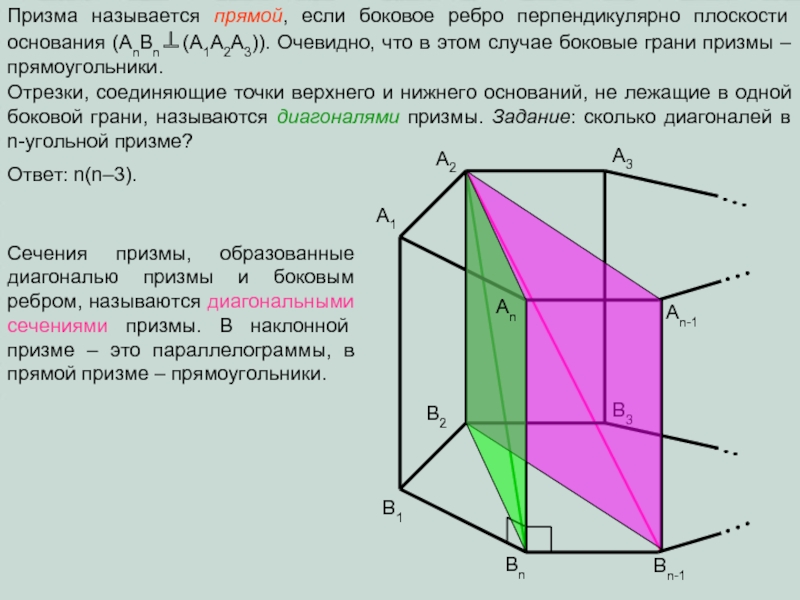
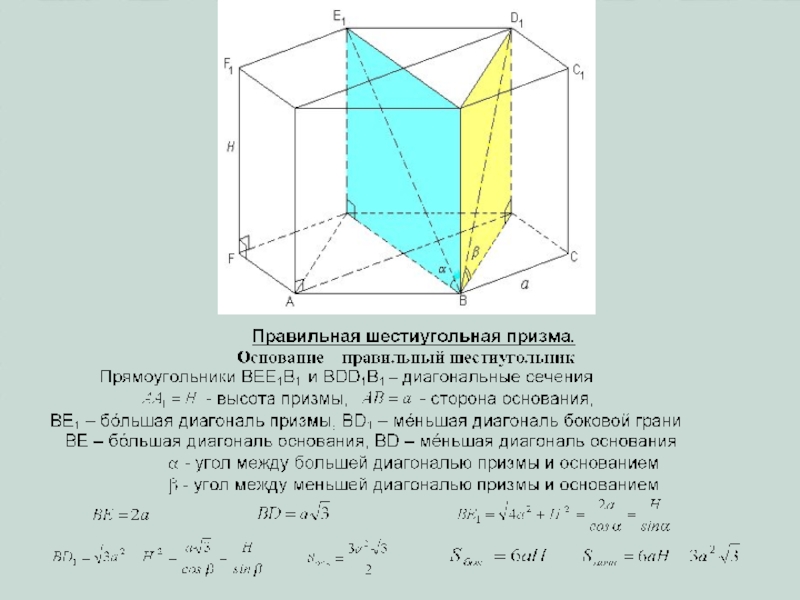
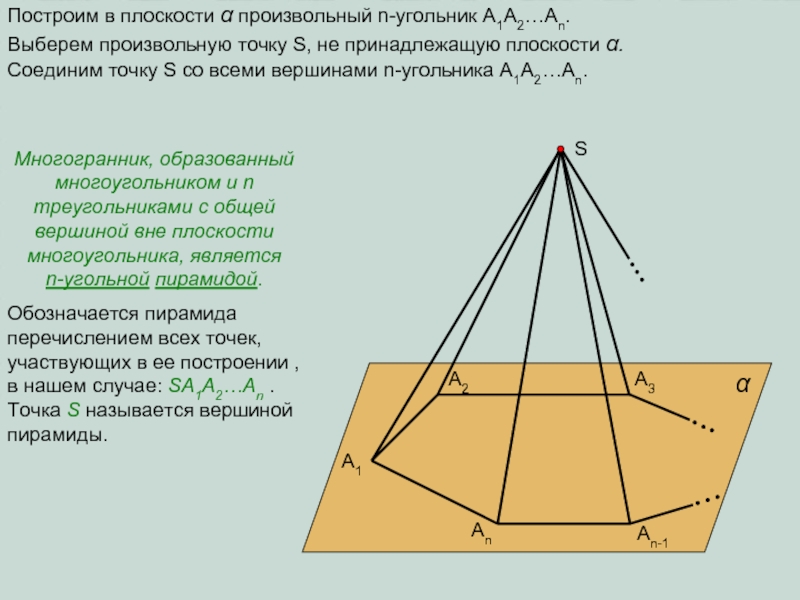
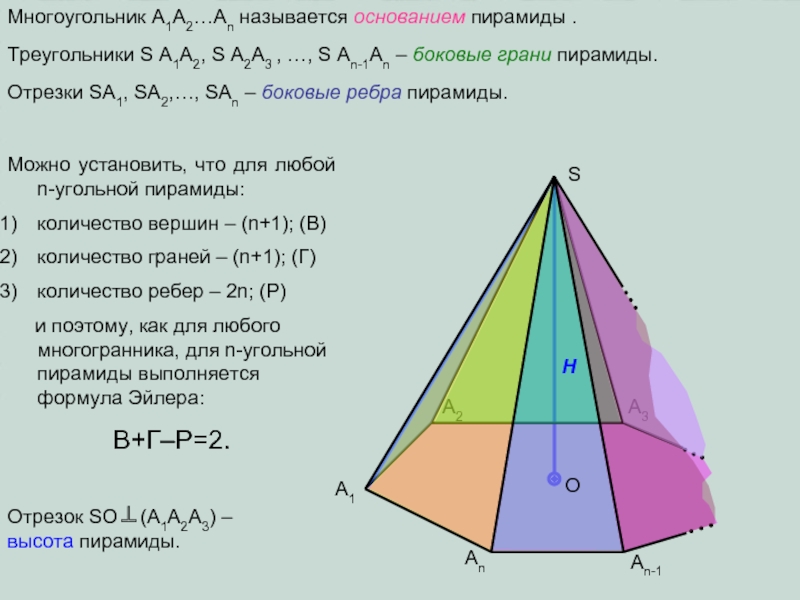
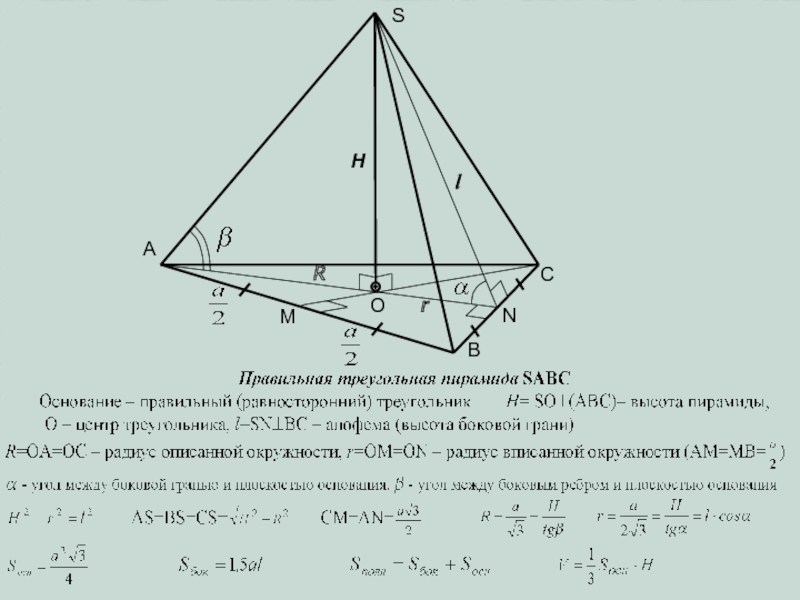
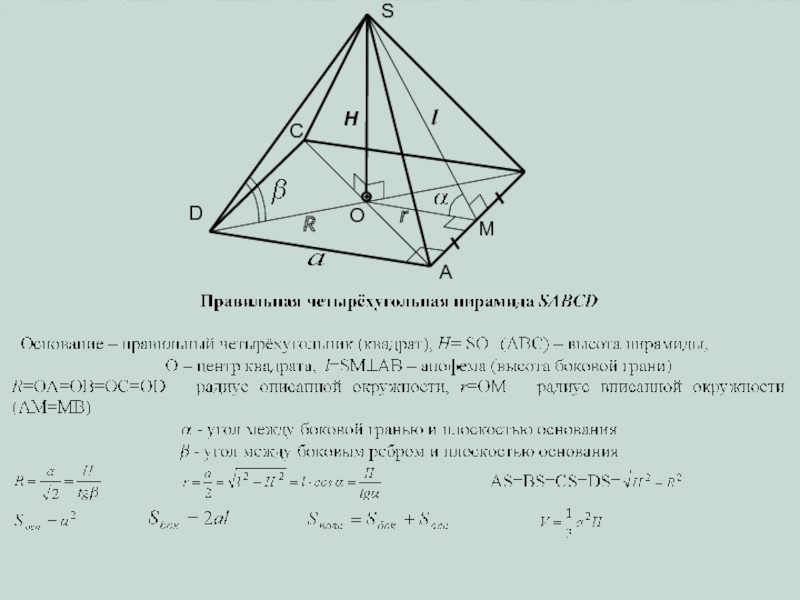
плоскости α произвольный n-угольник A1A2…An.
A1
A2
A3
An
An-1
α
β
B1
B2
B3
Bn
Bn-1
Через его вершины проведем параллельные

Соединив последовательно полученные точки получим n-угольник B1B2…Bn.

Многогранник, образованный двумя равными многоугольниками, лежащими в параллельных плоскостях и n параллелограммами является n-угольной призмой.
Обозначается призма перечислением всех точек, участвующих в ее построении , в нашем случае: A1A2…An B1B2…Bn.

нижней гранями n-угольной призмы).
Параллелограммы A1B1BnAn, A1B1B2A2 , …,AnBnBn-1An-1 – боковые

Параллельные и равные между собой отрезки A1B1, A2B2,…,AnBn – боковые ребра призмы.

Можно установить, что для любой n-угольной призмы:
количество вершин – 2n; (В)
количество граней – (n+2); (Г)
количество ребер – 3n; (Р)
и поэтому, как для любого многогранника, для n-угольной призмы выполняется формула Эйлера:
В+Г–Р=2.

An

An-1

H

O

Отрезок AnO⊥(B1B2B3) – высота призмы.

рисунке представлены треугольная (а), четырехугольная (б), пятиугольная (в), шестиугольная (г)

а)

б)

в)

г)

д)

Очевидно, что в этом случае боковые грани призмы – прямоугольники.
Отрезки,

A1

A2

A3

An-1

B1

B2

B3

Bn

Bn-1

Ответ: n(n–3).

Сечения призмы, образованные диагональю призмы и боковым ребром, называются диагональными сечениями призмы. В наклонной призме – это параллелограммы, в прямой призме – прямоугольники.

An

основания – правильные многоугольники. На рисунке представлены правильные

S, не принадлежащую плоскости α.
S
Соединим точку S со всеми вершинами

Многогранник, образованный многоугольником и n треугольниками с общей вершиной вне плоскости многоугольника, является n-угольной пирамидой.
Обозначается пирамида перечислением всех точек, участвующих в ее построении , в нашем случае: SA1A2…An . Точка S называется вершиной пирамиды.

, …, S An-1An – боковые грани пирамиды.
Отрезки SA1, SA2,…,

Можно установить, что для любой n-угольной пирамиды:
количество вершин – (n+1); (В)
количество граней – (n+1); (Г)
количество ребер – 2n; (Р)
и поэтому, как для любого многогранника, для n-угольной пирамиды выполняется формула Эйлера:
В+Г–Р=2.

H

O

Отрезок SO⊥(A1A2A3) – высота пирамиды.