Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямоугольный треугольник. Признаки равенства прямоугольных треугольников 7 класс
Содержание
- 1. Прямоугольный треугольник. Признаки равенства прямоугольных треугольников 7 класс
- 2. Тема урока: Прямоугольный треугольник. Признаки равенства прямоугольных треугольников.Тема урока: Прямоугольный треугольник. Признаки равенства прямоугольных треугольников.
- 3. Повторение. Тест. Домашние задачи у доски.Признаки равенства прямоугольных треугольников.Решение задач.План урока.
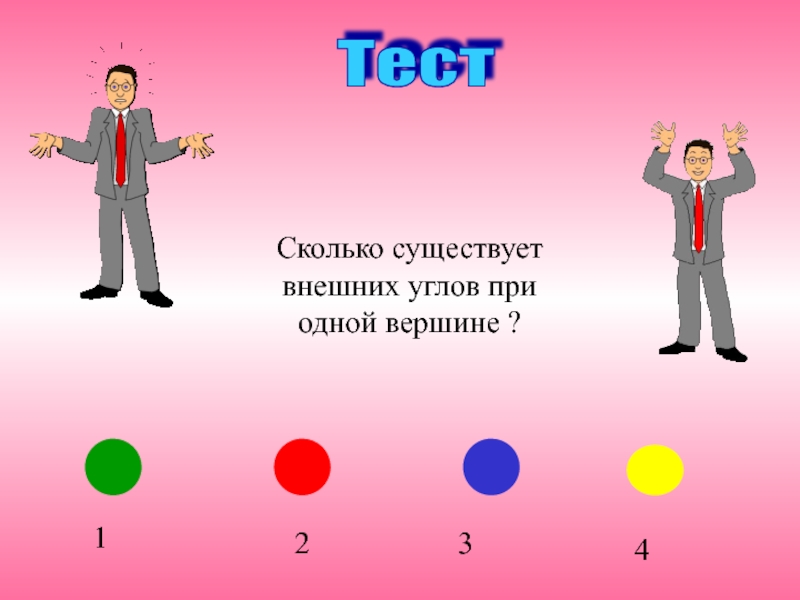
- 4. Тест 3124Сколько существует внешних углов при одной вершине ?
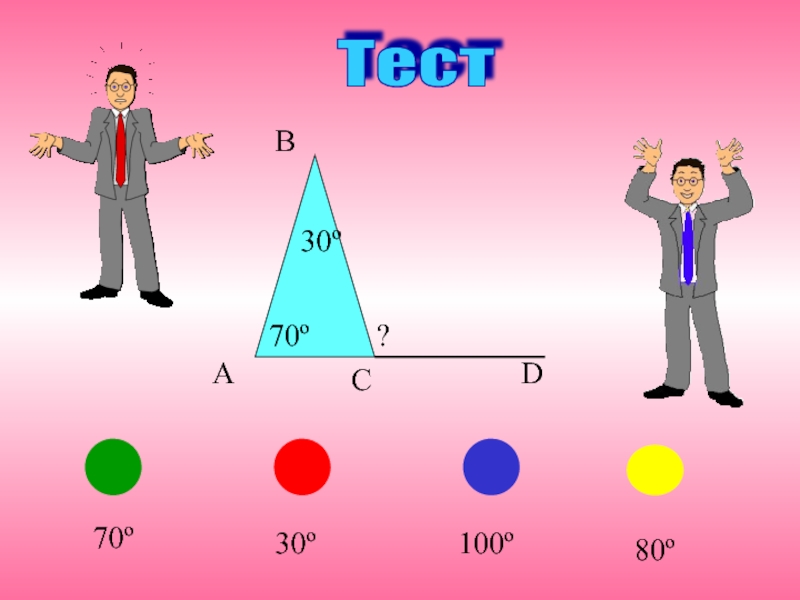
- 5. Тест 100º70º30º80º
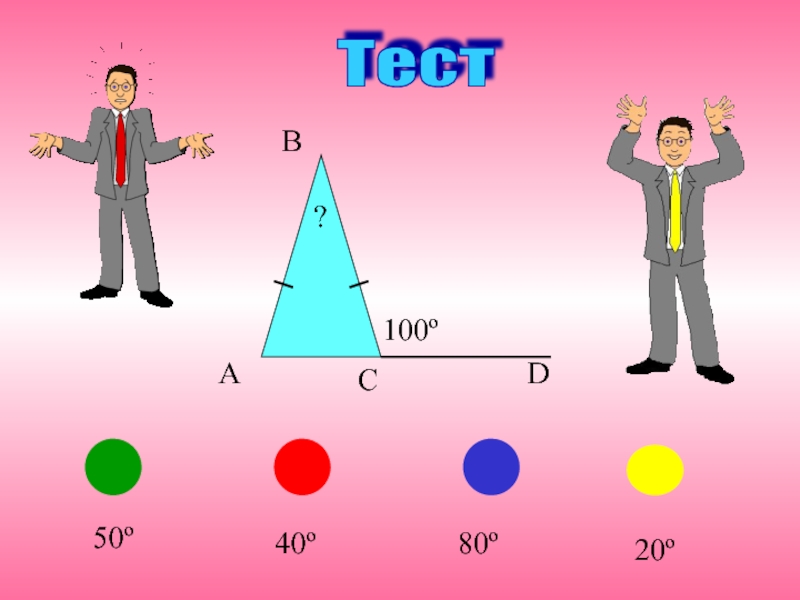
- 6. Тест ABCD?80º50º40º20º100º
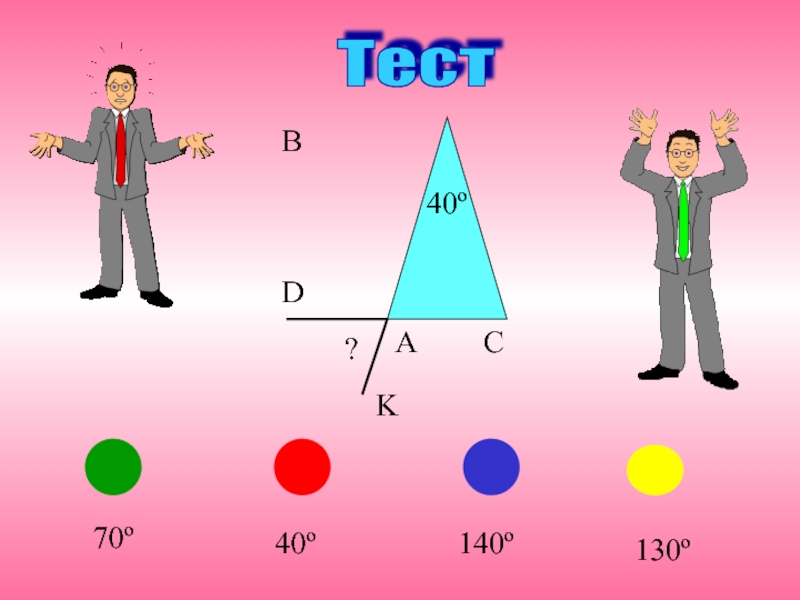
- 7. Тест B140º70º40º130ºK
- 8. Прямоугольный треугольникПрямоугольный треугольник
- 9. Треугольник называется прямоугольным, если у него есть
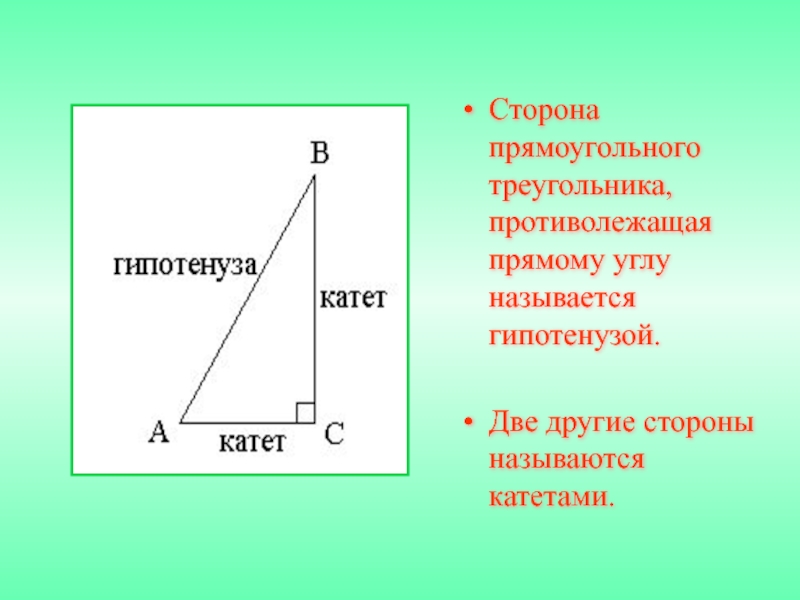
- 10. Сторона прямоугольного треугольника, противолежащая прямому углу называется гипотенузой.Две другие стороны называются катетами.
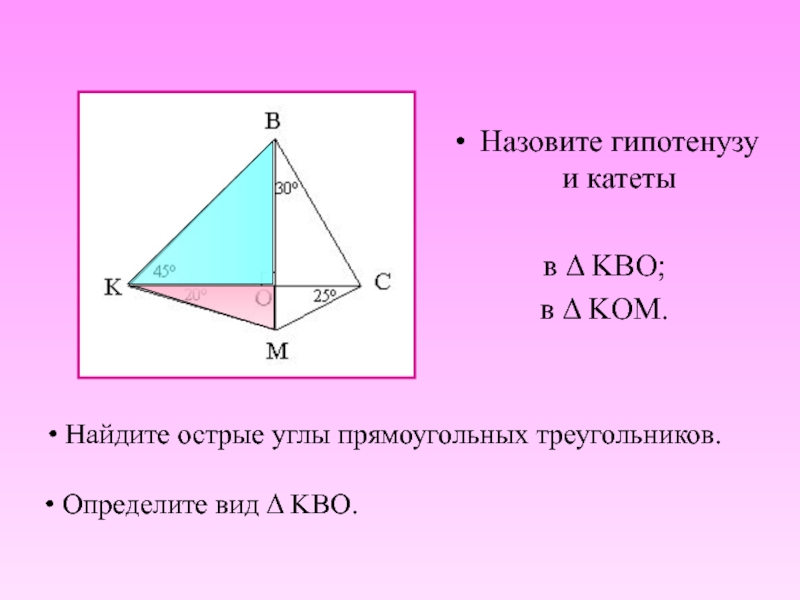
- 11. Найдите острые углы прямоугольных треугольников. Назовите
- 12. Признаки равенства прямоугольных треугольниковПризнаки равенства прямоугольных треугольников
- 13. Если два катета одного прямоугольного треугольника соответственно
- 14. Если гипотенуза и острый угол одного прямоугольного
- 15. Если катет и прилежащий к нему острый
- 16. Если катет и противолежащий острый угол одного
- 17. Если гипотенуза и катет одного прямоугольного треугольника
- 18. Домашнее задание Вопросы №14,15,16. Формулировки признаков. Задачи №40, 41(2).
- 19. Урок №2 по теме "Прямоугольный треугольник".
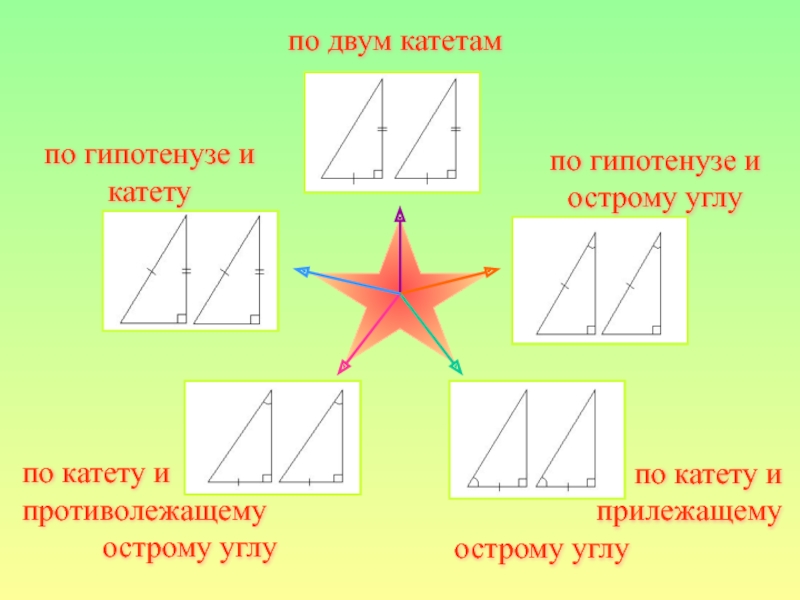
- 20. по двум катетампо гипотенузе и острому углупо
- 21. Тест Выбери правильное завершение определения.Катетом называется…Любая сторона
- 22. Тест Выбери правильное завершение определения.Гипотенузой называется…Любая сторона
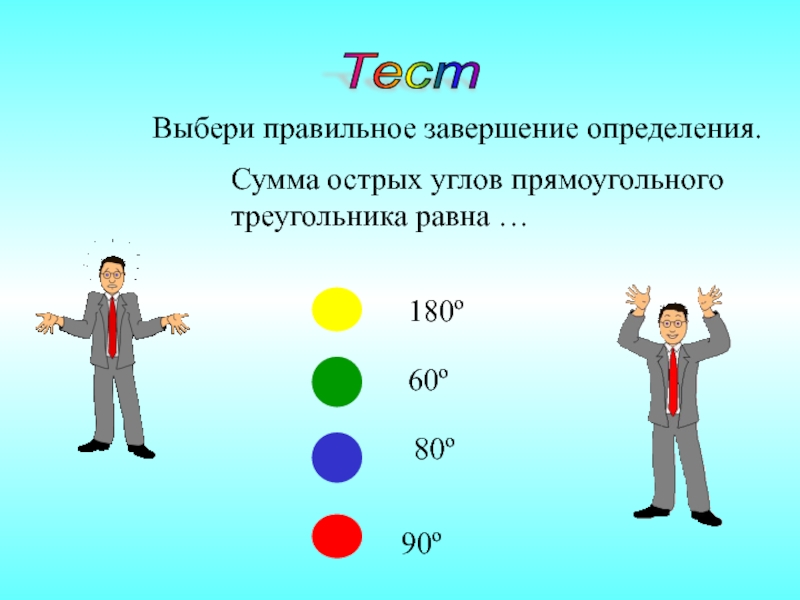
- 23. Тест Выбери правильное завершение определения.Сумма острых углов прямоугольного треугольника равна …
- 24. Тест 153º63º73º27ºABC27º?
- 25. Чему равны углы при основании в
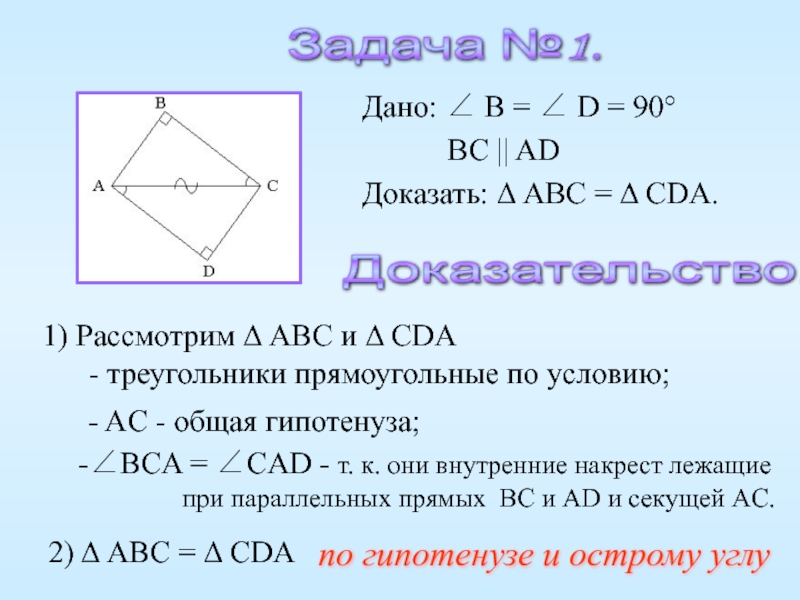
- 26. Задача №1. Доказательство. 1) Рассмотрим Δ
- 27. Из точки D, лежащей на биссектрисе ∠
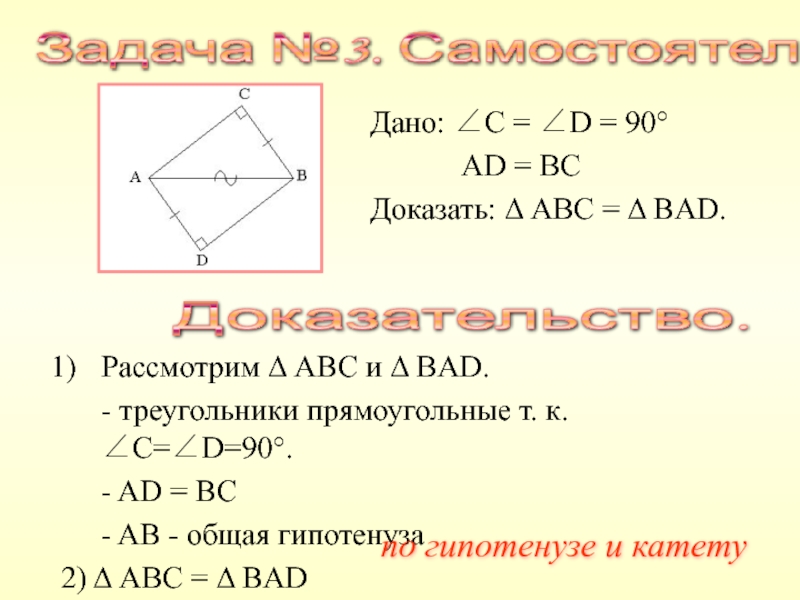
- 28. Дано: ∠C = ∠D = 90°
- 29. Задача №4. Решение. 1) Рассмотрим ΔABO и
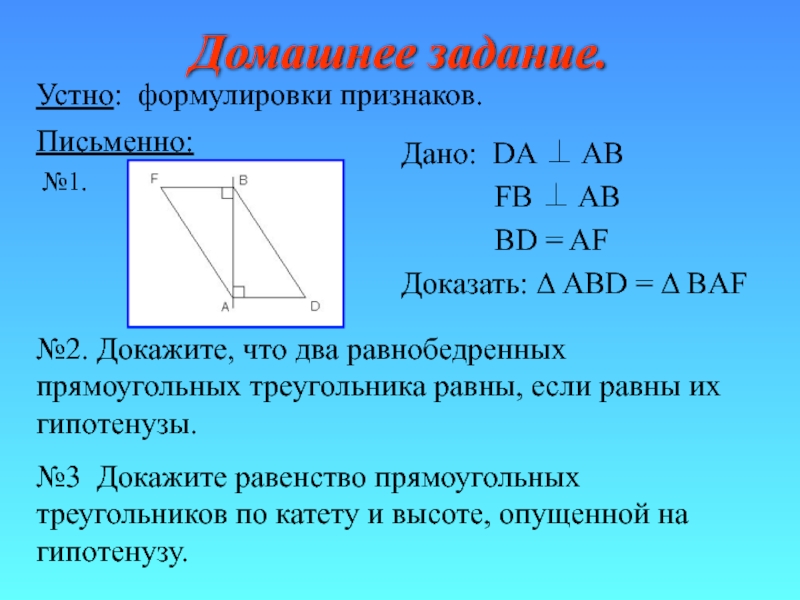
- 30. Домашнее задание.Дано: DA ⊥ AB
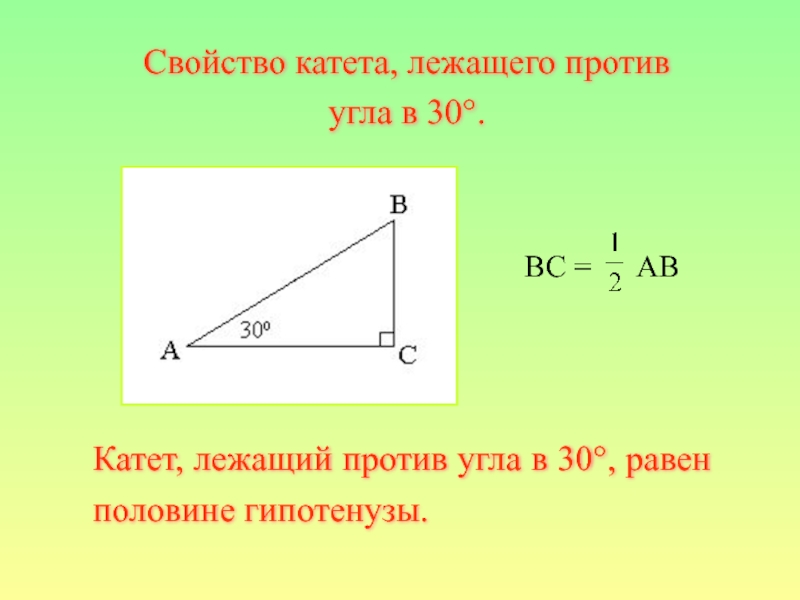
- 31. Cвойство катета, лежащего против угла в 30 градусов. Тема урока
- 32. BC
- 33. Дано: Δ ABC
- 34. Дано: Δ ABC - равнобедренный
- 35. Решение. Δ ABC – равнобедренный
- 36. по двум катетампо гипотенузе и острому углупо
- 37. Докажите, что у равных треугольников высоты, проведенные
- 38. Повторение. №2. Докажите, что сумма трех внешних
- 39. Домашнее задание.Устно: формулировки признаков и формулировка
- 40. BC
- 41. Скачать презентанцию
Тема урока: Прямоугольный треугольник. Признаки равенства прямоугольных треугольников.Тема урока: Прямоугольный треугольник. Признаки равенства прямоугольных треугольников.
Слайды и текст этой презентации
Слайд 2Тема урока:
Прямоугольный треугольник.
Признаки равенства прямоугольных треугольников.
Тема урока:
Прямоугольный треугольник.
Признаки равенства прямоугольных
треугольников.
Слайд 3Повторение. Тест.
Домашние задачи у доски.
Признаки равенства прямоугольных треугольников.
Решение
задач.
План урока.
Слайд 9Треугольник называется прямоугольным, если у него есть прямой угол.
ABC – прямоугольный
∠ C = 90°
∠ A + ∠ B = 90°
Сумма острых углов прямоугольного треугольника равна 90°.
Определение.
Слайд 10Сторона прямоугольного треугольника, противолежащая прямому углу называется гипотенузой.
Две другие стороны
называются катетами.
Слайд 11
Найдите острые углы прямоугольных треугольников.
Назовите гипотенузу и катеты
в Δ
KBO;
в Δ KOM.
Определите вид Δ KBO.
Слайд 12Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Слайд 13Если два катета одного прямоугольного треугольника соответственно равны двум катетам
другого прямоугольного треугольника, то такие треугольники равны.
по двум катетам
по двум
сторонам и углу между ними
Слайд 14Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны
гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники
равны. по гипотенузе и
острому углу
по стороне и двум
прилежащим к ней углам
Слайд 15Если катет и прилежащий к нему острый угол одного прямоугольного
треугольника соответственно равны катету и прилежащему к нему острому углу
другого прямоугольного треугольника, то такие треугольники равны.по катету и прилежащему острому углу
по стороне и двум прилежащим к ней углам
Слайд 16Если катет и противолежащий острый угол одного прямоугольного треугольника соответственно
равны катету и противолежащему острому углу другого прямоугольного треугольника, то
такие треугольники равны.по катету и противолежащему острому углу
по стороне и двум прилежащим углам
Слайд 17Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе
и катету другого прямоугольного треугольника, то такие треугольники равны.
по гипотенузе
и катету
Слайд 20по двум катетам
по гипотенузе и острому углу
по катету и
прилежащему
острому углу
по катету и
противолежащему
острому углу
по гипотенузе и катету
Слайд 21Тест
Выбери правильное завершение определения.
Катетом называется…
Любая сторона треугольника;
Сторона, лежащая против
прямого угла треугольника;
Перпендикуляр из вершины угла на противолежащую сторону;
Сторона, примыкающая
к вершине прямого угла.
Слайд 22Тест
Выбери правильное завершение определения.
Гипотенузой называется…
Любая сторона треугольника;
Сторона, лежащая против
прямого угла треугольника;
Перпендикуляр из вершины угла на противолежащую сторону;
Сторона, примыкающая
к вершине прямого угла.
Слайд 23Тест
Выбери правильное завершение определения.
Сумма острых углов прямоугольного треугольника равна
Слайд 25 Чему равны углы при основании в равнобедренном
прямоугольном
треугольнике?
Могут ли в равнобедренном прямоугольном
треугольнике углы при основании
быть равными 90°?
Слайд 26
Задача №1.
Доказательство.
1) Рассмотрим Δ ABC и Δ
CDA
- треугольники прямоугольные по условию;
Слайд 27Из точки D, лежащей на биссектрисе ∠ A, опущены перпендикуляры
DB и DC на стороны угла. Докажите, что Δ ADB
= Δ ADC.Задача №2.
Доказательство.
1) Рассмотрим Δ ADB и Δ ADC.
- треугольники прямоугольные т. к. DB⊥AB, DC⊥AC.
2) Δ ADB = Δ ADC по гипотенузе и острому углу.
- AD - общая гипотенуза.
Слайд 29Задача №4.
Решение.
1) Рассмотрим ΔABO и ΔDCO.
2) ΔABO =
ΔDCO по гипотенузе и острому углу.
3) Из равенства
треугольников следует AB = CD = 3 см.• AO = OD т. к. O - середина AD.
• треугольники прямоугольные т. к. AB⊥BC и CD⊥BC.
Слайд 30Домашнее задание.
Дано: DA ⊥ AB
FB ⊥ AB
BD
= AF Доказать: Δ ABD = Δ BAF
Устно: формулировки признаков.
№1.
№2. Докажите, что два равнобедренных прямоугольных треугольника равны, если равны их гипотенузы.
№3 Докажите равенство прямоугольных треугольников по катету и высоте, опущенной на гипотенузу.
Письменно:
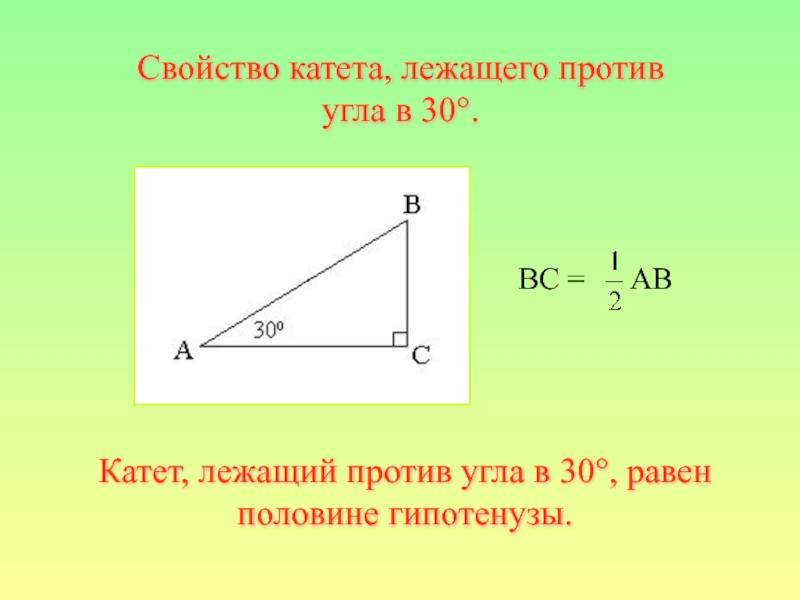
Слайд 32 BC =
AB
Катет, лежащий против угла в 30°, равен половине гипотенузы.
Свойство катета,
лежащего против угла в 30°.
Слайд 33Дано: Δ ABC
∠
C = 90°, ∠ B = 30°.
Доказать: АС =
АВ.Докажите, что в прямоугольном треугольнике с углом 30° катет, противолежащий этому углу, равен половине гипотенузы.
Доказательство.
Задача №43
Слайд 34Дано: Δ ABC - равнобедренный
с
основанием AC;
∠ B =120°;
BD - медиана; BD = 3 см.Найти: ∠ A, ∠ C, AB и BC.
Задача №1.
Решение.
В равнобедренном треугольнике угол, противолежащий основанию, равен 120°, а медиана, проведенная к основанию, равна 3 см. Найдите углы при основании и боковые стороны треугольника.
1) Δ ABC - равнобедренный по условию.
BD - медиана, биссектриса и высота.
Слайд 35Решение.
Δ ABC – равнобедренный
по условию.
BD
- медиана, биссектриса и высота.3) Δ ABD - прямоугольный т. к. ∠ADB = 90°.
5) BD = AB по свойству катета, лежащего против угла в 30°.
AB = 3 • 2 = 6 см. AB = BC = 6 см.
6) ∠A = ∠C = 30° как углы при основании равнобедренного
треугольника.
Слайд 36по двум катетам
по гипотенузе и острому углу
по катету и
прилежащему
острому углу
по катету и
противолежащему
острому углу
по гипотенузе и катету
Слайд 37Докажите, что у равных треугольников высоты, проведенные из соответствующих вершин,
равны.
Задача №1.
Доказательство.
2) ΔABD = ΔA1B1D1 по
гипотенузе и острому углу.3) Из равенства треугольников следует BD = B1D1.
Слайд 38Повторение.
№2.
Докажите, что сумма трех внешних углов треугольника, взятых
по одному при каждой вершине, равна 360º.
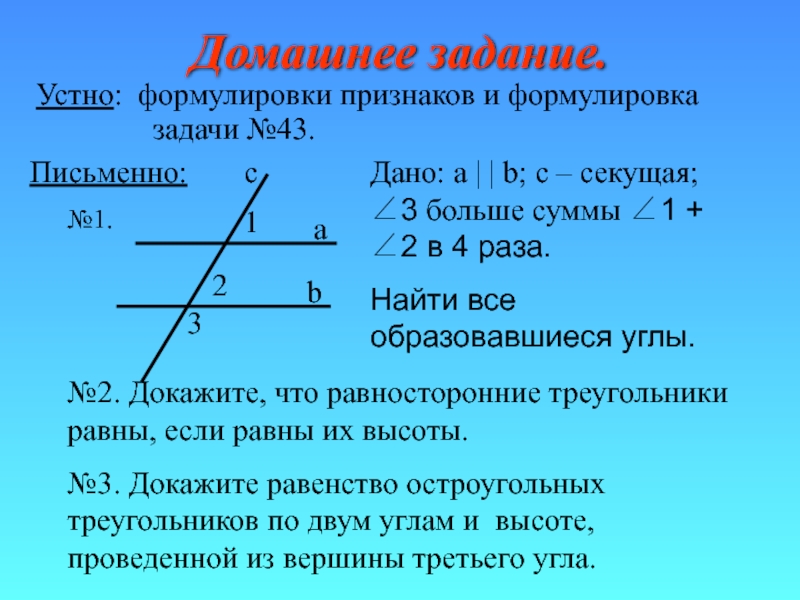
Слайд 39Домашнее задание.
Устно: формулировки признаков и формулировка
задачи №43.
№1.
№2. Докажите, что равносторонние треугольники равны,
если равны их высоты.№3. Докажите равенство остроугольных треугольников по двум углам и высоте, проведенной из вершины третьего угла.
Письменно:
1
2
3
a
b
c
Дано: a | | b; с – секущая; ∠3 больше суммы ∠1 + ∠2 в 4 раза.
Найти все образовавшиеся углы.
Слайд 40 BC =
AB
Катет, лежащий против угла в 30°, равен половине гипотенузы.
Свойство катета,
лежащего против угла в 30°.
