Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Радианная мера угла
Содержание
- 1. Радианная мера угла
- 2. 11Радианная мера угла1 радианУгол в 1 радиан
- 3. № 1.2.1
- 4. № 1.2.2
- 5. № 1.2.3
- 6. № 1.2.4
- 7. Точки B, C, D, F, E делят
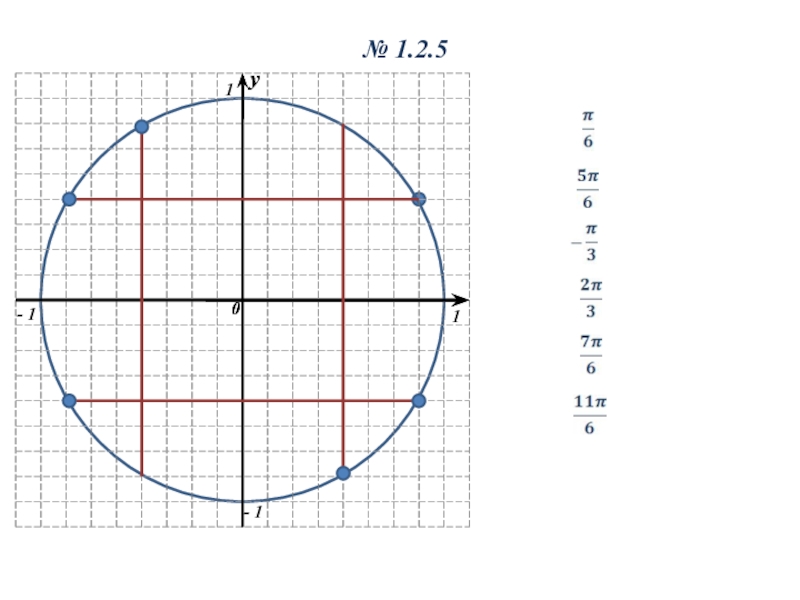
- 8. № 1.2.5
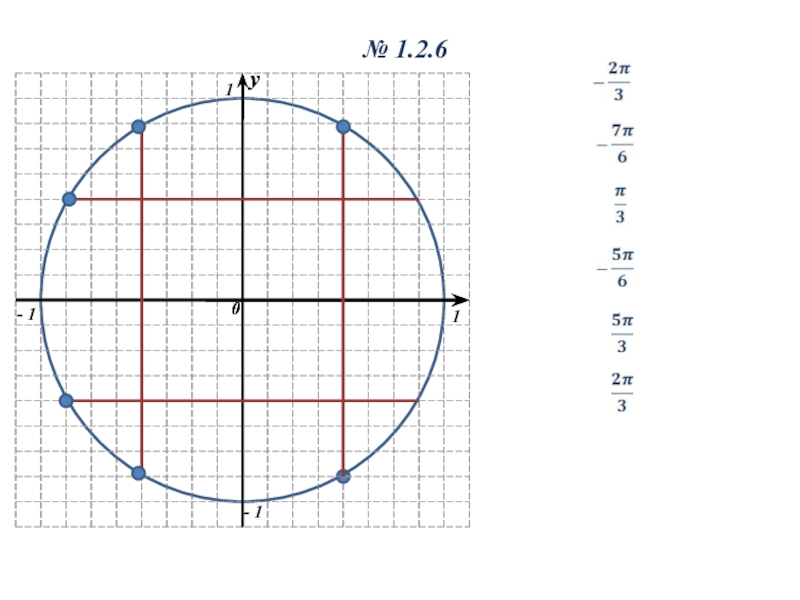
- 9. № 1.2.6
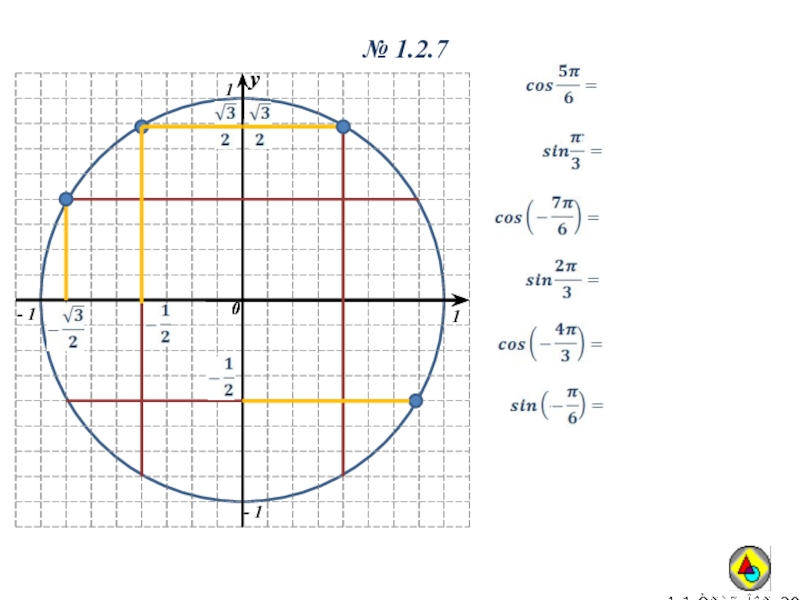
- 10. № 1.2.7
- 11. № 1.2.8
- 12. № 1.2.9
- 13. № 1.2.10
- 14. Точки B, C, D делят дугу AF
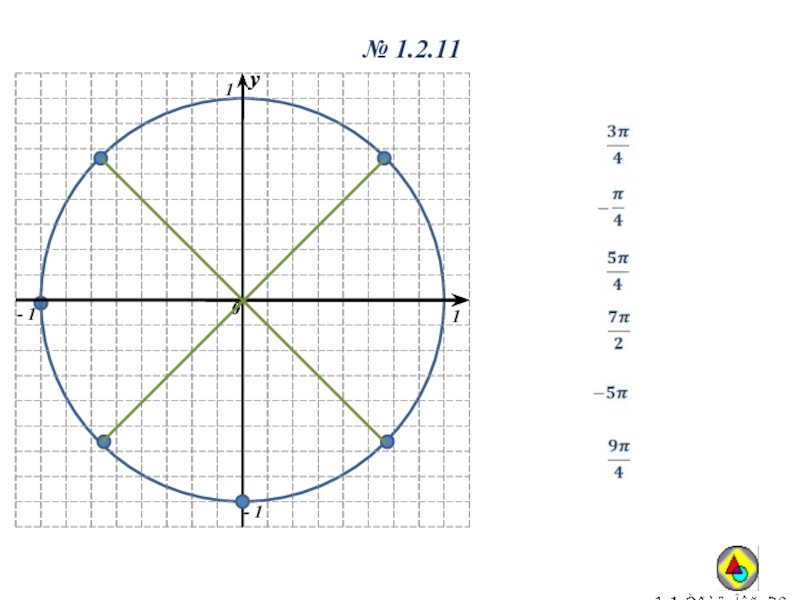
- 15. № 1.2.11
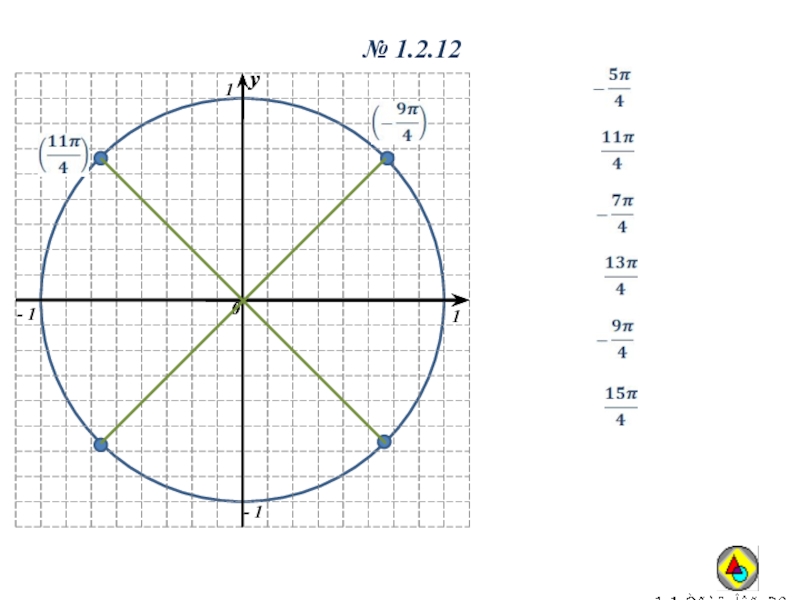
- 16. № 1.2.12
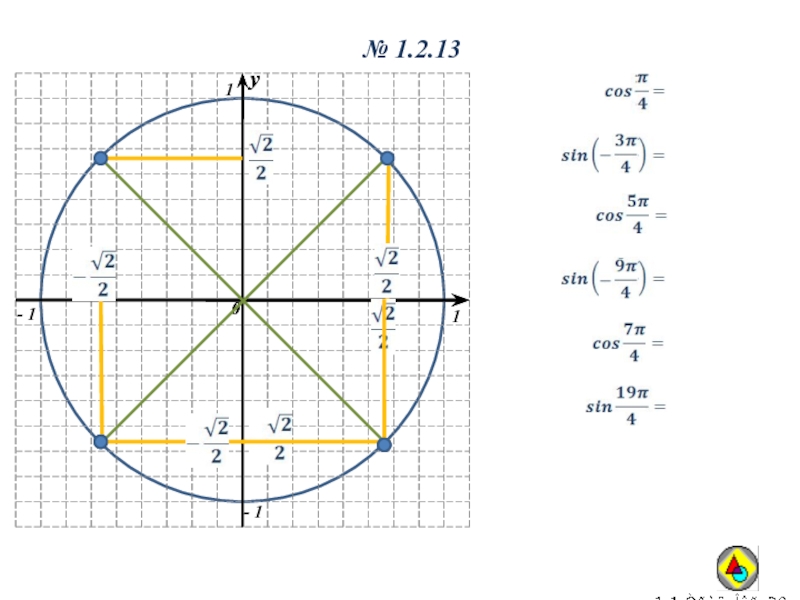
- 17. № 1.2.13
- 18. № 1.2.14
- 19. № 1.2.15
- 20. № 1.2.16
- 21. № 1.2.17
- 22. № 1.2.18
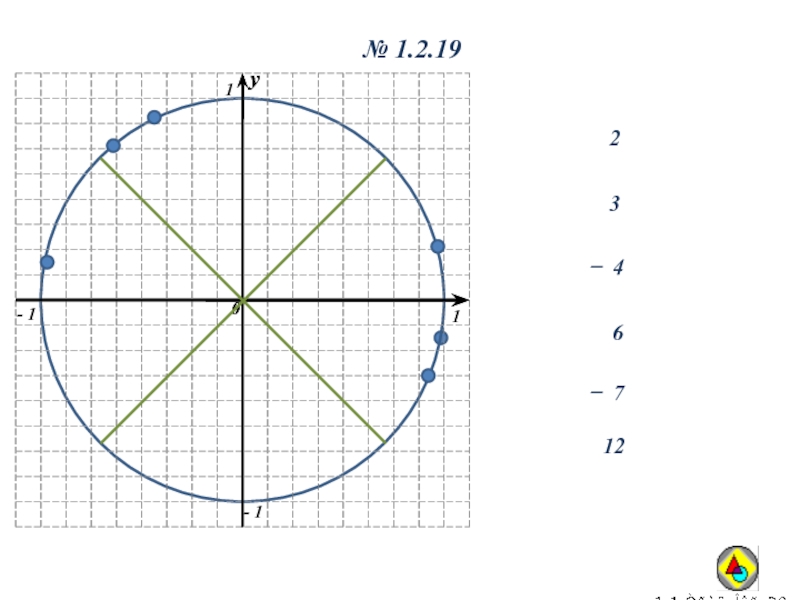
- 23. № 1.2.1923̶ 4̶ 7612
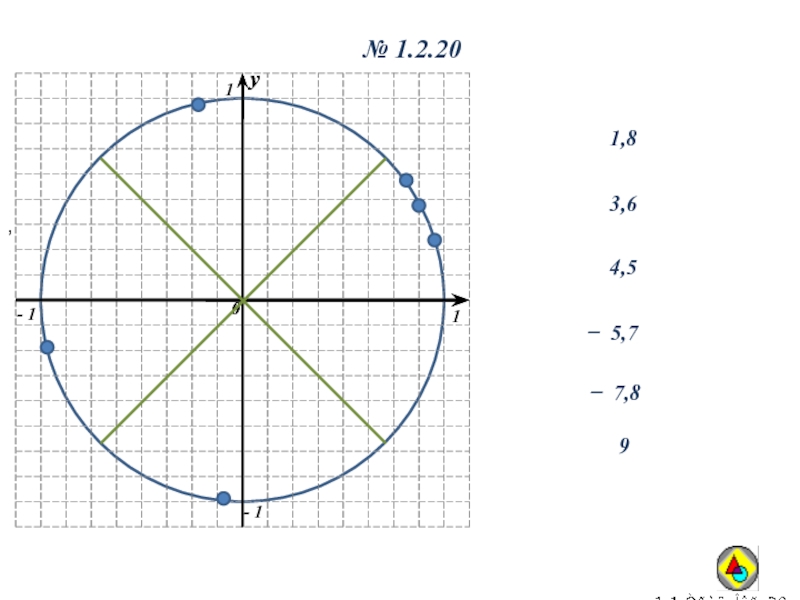
- 24. № 1.2.20,1,83,64,5̶ 7,8̶ 5,79
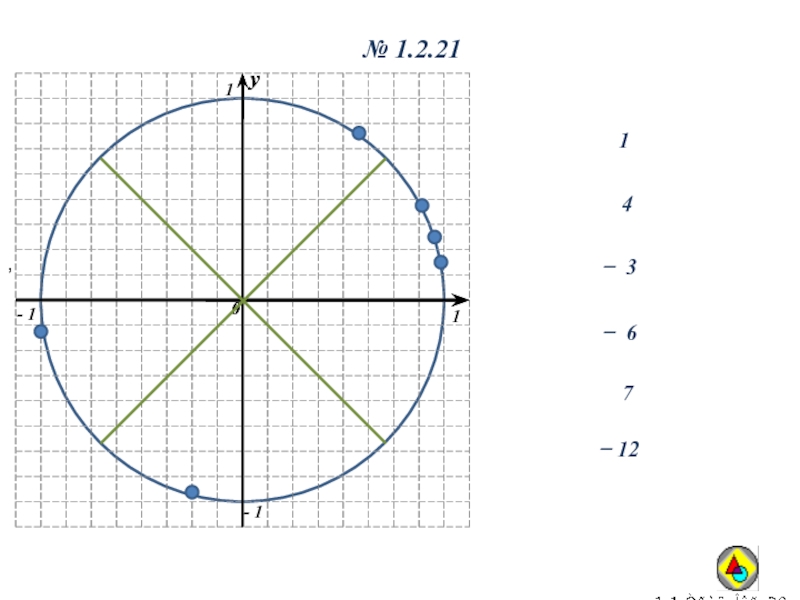
- 25. ,№ 1.2.2114̶ 37̶ 6̶ 12
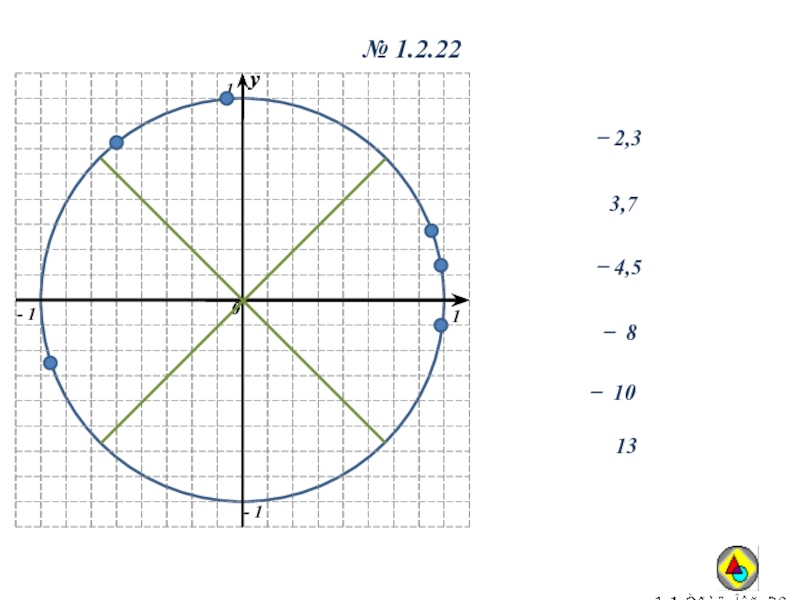
- 26. № 1.2.22̶ 2,33,7̶ 4,5̶ 10̶ 813
- 27. 1,9 ϵ IVчетверти№ 1.2.23̶ 3,8 ϵ5 ϵ17 ϵ̶ 1,3 ϵ̶ 2,8 ϵII четверти IVчетверти IVчетверти IVчетвертиIIIчетверти
- 28. ̶ 5,4 ϵIIIчетверти IVчетверти№ 1.2.242,8 ϵ3,4
- 29. Скачать презентанцию
11Радианная мера угла1 радианУгол в 1 радиан – это центральный угол окружности, который соответствует дуге, равной радиусу.
Слайды и текст этой презентации
Слайд 1
1
1
2
2
3
3
4
4
5
5
6
6
7
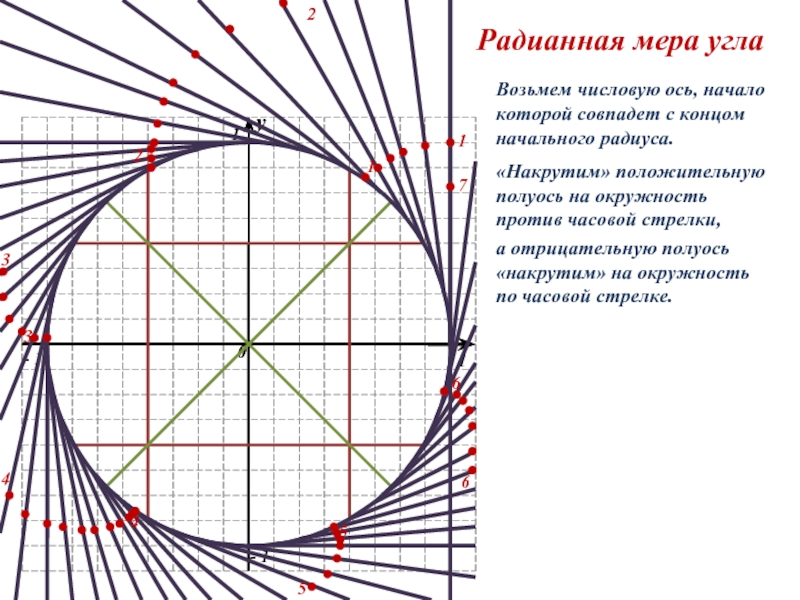
Радианная мера угла
Возьмем числовую ось, начало которой совпадет с концом
начального радиуса.
полуось «накрутим» на окружность по часовой стрелке.Слайд 2
1
1
Радианная мера угла
1 радиан
Угол в 1 радиан – это центральный
угол окружности, который соответствует дуге, равной радиусу.
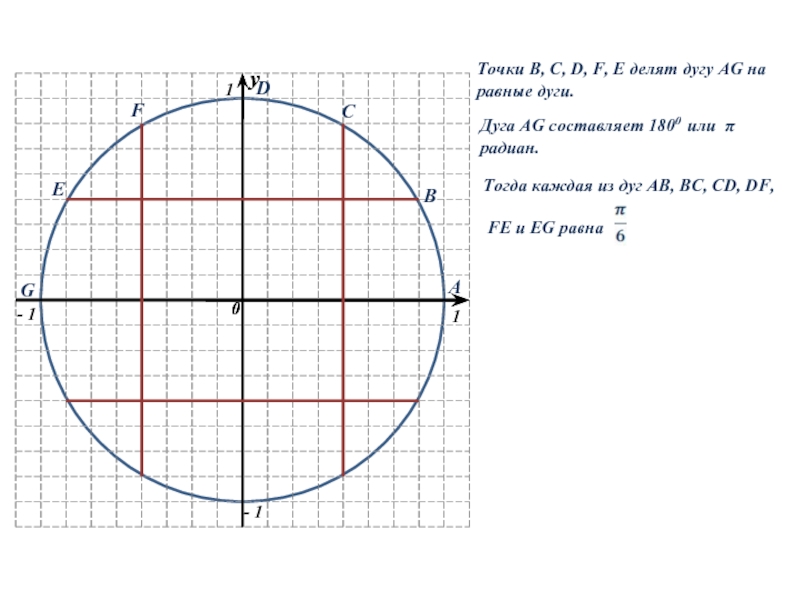
Слайд 7Точки B, C, D, F, E делят дугу AG на
равные дуги.
Дуга AG составляет 1800 или π радиан.
Тогда каждая из
дуг AB, BC, CD, DF,FE и EG равна
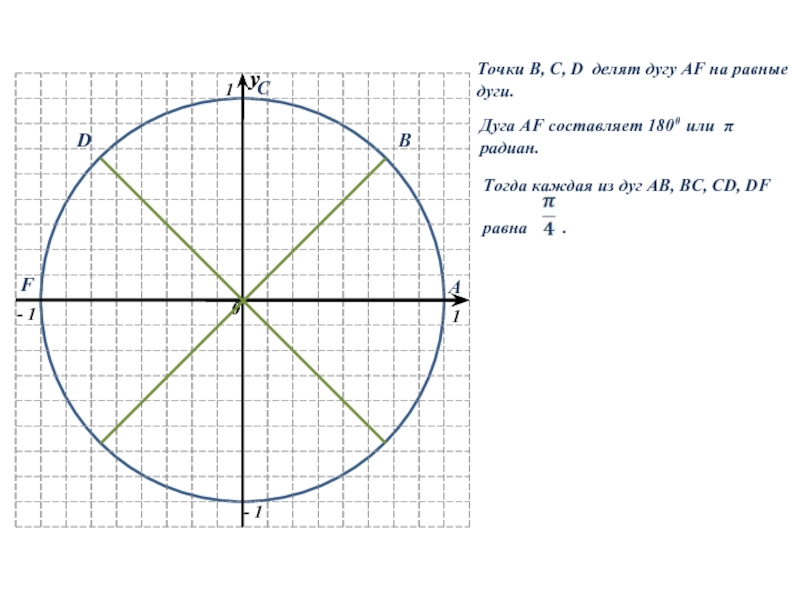
Слайд 14Точки B, C, D делят дугу AF на равные дуги.
Дуга
AF составляет 1800 или π радиан.
Тогда каждая из дуг AB,
BC, CD, DFравна .
Слайд 271,9 ϵ
IVчетверти
№ 1.2.23
̶ 3,8 ϵ
5 ϵ
17 ϵ
̶ 1,3 ϵ
̶
2,8 ϵ
II четверти
IVчетверти
IVчетверти
IVчетверти
IIIчетверти
Слайд 28̶ 5,4 ϵ
IIIчетверти
IVчетверти
№ 1.2.24
2,8 ϵ
3,4 ϵ
̶ 9 ϵ
16
ϵ
̶ 10 ϵ
I четверти
II четверти
I четверти
IVчетверти
Теги