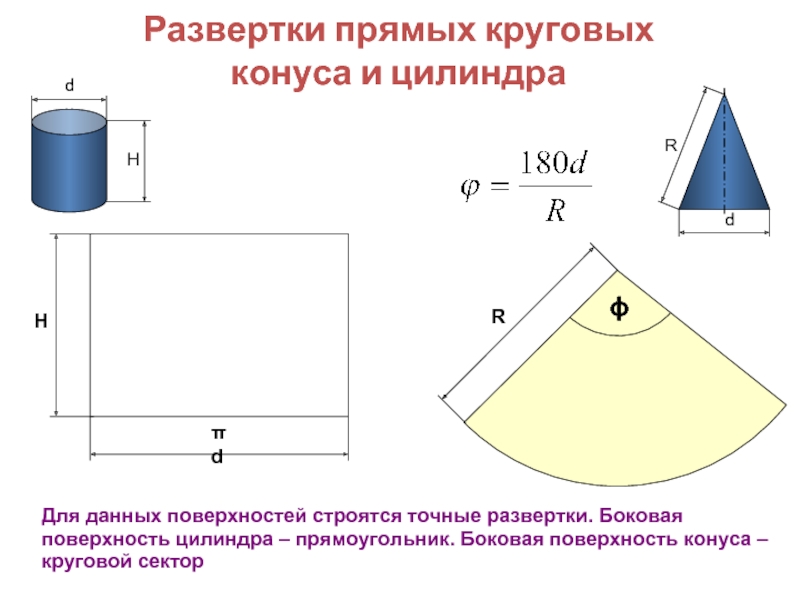
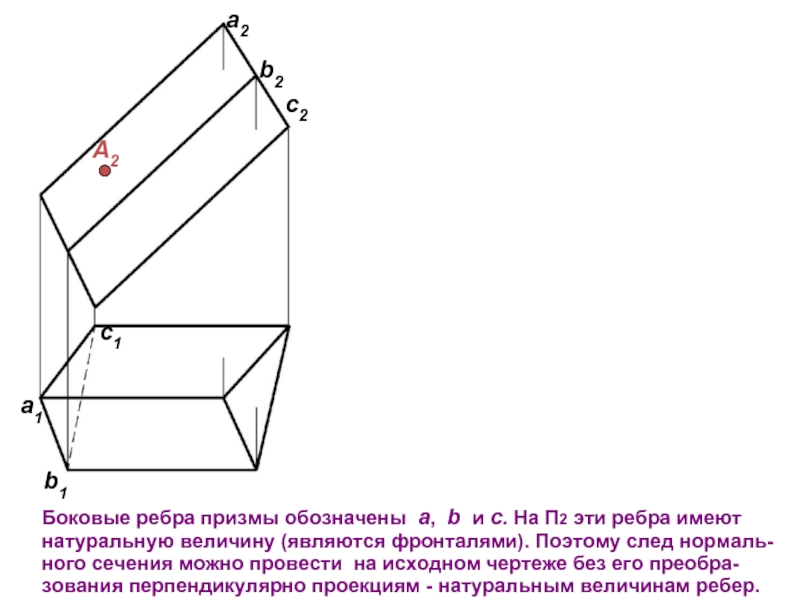
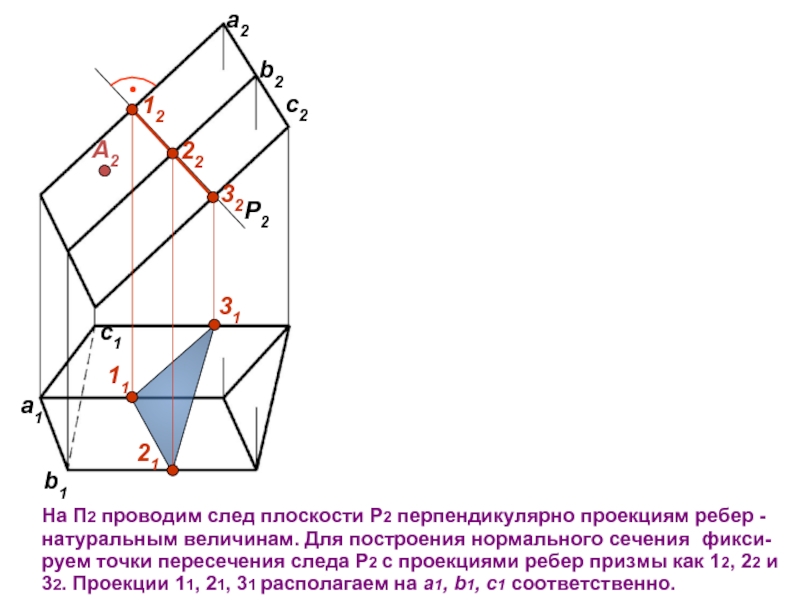
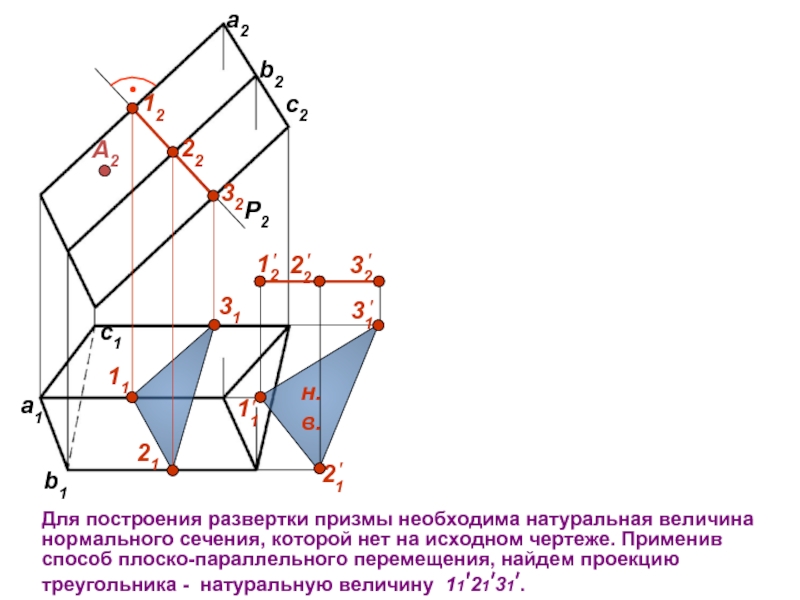
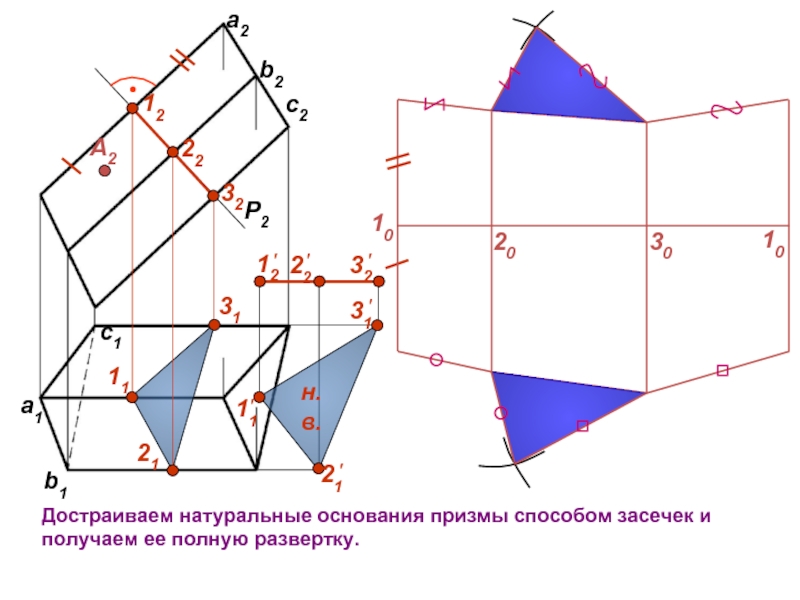
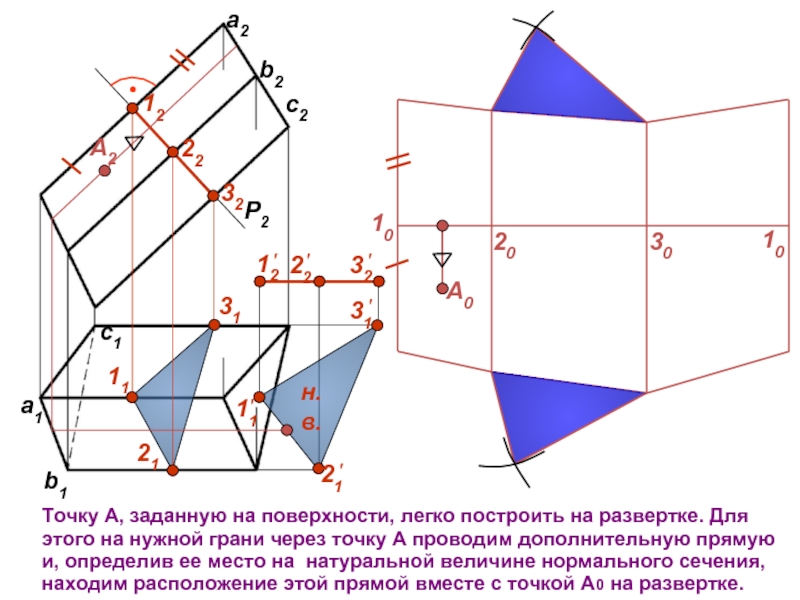
совмещаются с плоскостью.
Развертка - плоская фигура, получаемая в результате данного
преобразования.Поверхности делятся на развертываемые и неразвертываемые.
Развертываемые совмещаются с плоскостью без разрывов и складок
Для неразвертываемых строятся условные развертки