Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Волшебный мир сечений 10-11 класс
Содержание
- 1. Волшебный мир сечений 10-11 класс
- 2. Элективный курс «Использование сечений в стереометрии»Цели
- 3. Слайд 3
- 4. Слайд 4
- 5. Результативность опытаЕГЭ.Олимпиады.Конкурсы, конференции.Поступление в вузы.Профориентация.
- 6. ЕГЭ
- 7. Конкурсы
- 8. Конкурсы
- 9. ВОЛШЕБНЫЙ МИР СЕЧЕНИЙ
- 10. Построение сечений Построить сечение многогранника плоскостью –
- 11. Метод следовСуть метода : построить
- 12. XY – след секущей плоскости
- 13. Метод внутреннего проектирования (МВП)Сущность метода: нахождение
- 14. Построить сечение призмы плоскостью, проходящей через точки
- 15. Комбинированный метод Сущность этого метода состоит
- 16. Дан куб .Через точки М, К
- 17. Группа1. Постройте сечение пирамиды, плоскостью, проходящей через заданные точки.АBCDSMNKXPYQ
- 18. Группа 2. Постройте сечение
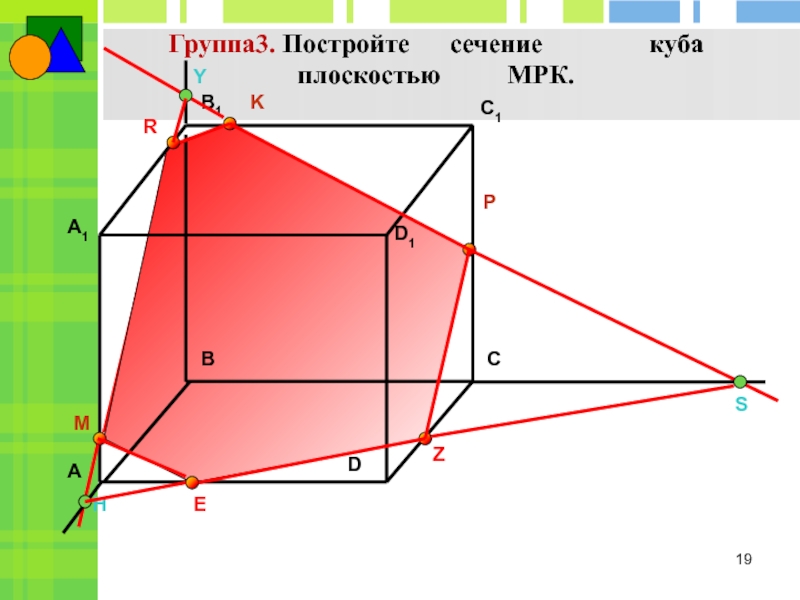
- 19. Группа3. Постройте сечение
- 20. Группа 4. Постройте сечение
- 21. Группа 5. Постройте сечение
- 22. Группа 6. Постройте сечение
- 23. Классификация задач:Нахождение площади сечений в многогранниках.Нахождение расстояния
- 24. Группа 1. В прямоугольном параллелепипеде ABCDA1B1C1D1
- 25. Группа 2.В правильной треугольной призме ABCA1B1C1 стороны основания
- 26. Группа 3.В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания
- 27. Группа 4.В правильной четырёхугольной пирамиде MABCD с вершиной
- 28. Группа 5.В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания
- 29. Группа 6.В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра AB=4,
- 30. Слайд 30
- 31. СПАСИБО ЗА СОТРУДНИЧЕСТВО!
- 32. Скачать презентанцию
Элективный курс «Использование сечений в стереометрии»Цели курса:Обучение учащихся методам построения (изображения) пространственных фигур на плоскости.Обучение учащихся методам решения задач на построение сечений многогранника.
Слайды и текст этой презентации
Слайд 1Мастер-класс в рамках работы ресурсного центра на базе МБОУ гимназии
городского округа г.Урюпинск
Слайд 2Элективный курс
«Использование сечений в стереометрии»
Цели курса:
Обучение учащихся методам построения
(изображения) пространственных фигур на плоскости.
Обучение учащихся методам решения задач на
построение сечений многогранника.Слайд 10Построение сечений
Построить сечение многогранника плоскостью – это значит построить
прямые, являющиеся следами пересечения граней многогранника данной плоскостью.
Секущая плоскость может
быть задана различными способами:- тремя точками, не лежащими на одной прямой;
- прямой и точкой, не лежащей на ней;
- двумя пересекающимися или параллельными прямыми …
Для построения сечений многогранников плоскостью применяются три метода:
- построения следов;
- метод внутреннего проектирования;
- комбинированный метод.
Слайд 11Метод следов
Суть метода :
построить вспомогательную прямую,
которая является изображением линии пересечения секущей плоскости с плоскостью какой-либо
грани фигуры . Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигурыСлайд 12
XY – след секущей плоскости
на
плоскости основания
D
C
B
Z
Y
X
M
N
P
S
Постройте сечение пирамиды плоскостью,
проходящей через три точки M,N,P.
А
F
Слайд 13Метод внутреннего проектирования (МВП)
Сущность метода:
нахождение по известным элементам
сечения в объёмной фигуре их проекций и по проекциям элементов
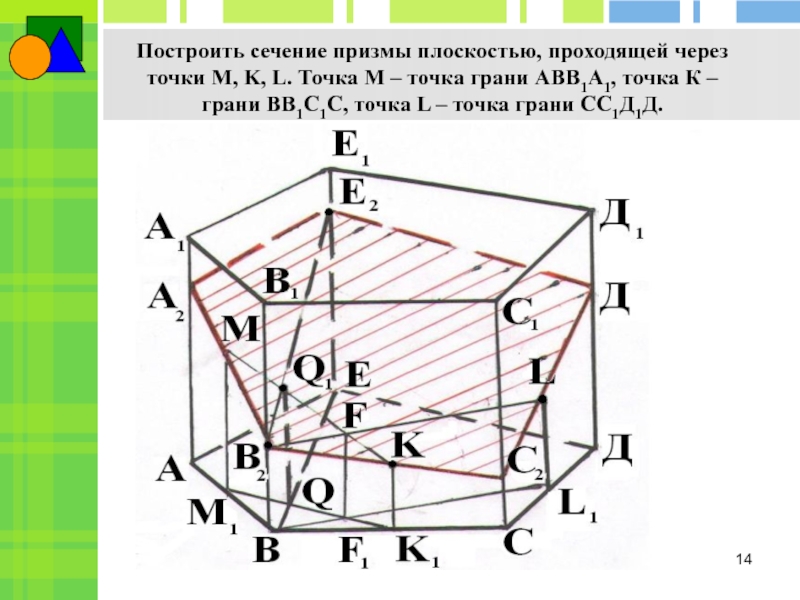
сечения – самих сеченийСлайд 14Построить сечение призмы плоскостью, проходящей через точки M, K, L.
Точка M – точка грани АВВ1А1, точка К – грани
ВВ1С1С, точка L – точка грани СС1Д1Д.Слайд 15Комбинированный метод
Сущность этого метода состоит в том, что
на некоторых этапах построения сечения применяется или метод следов, или
метод внутреннего проецирования, а на других этапах построения этого сечения осуществляется с использованием теорем о параллельности в пространстве и других.Слайд 16
Дан куб .Через точки М, К и середину Е
проведена секущая плоскость. (Постройте сечение )
М
Е
К
м1
L
X
Т
P
J
Z
Слайд 17
Группа1. Постройте сечение пирамиды, плоскостью, проходящей через заданные точки.
А
B
C
D
S
M
N
K
X
P
Y
Q
Слайд 23Классификация задач:
Нахождение площади сечений в многогранниках.
Нахождение расстояния и угла между
скрещивающимися прямыми в многогранниках.
Определение угла между плоскостями.
Отношение объемов частей многогранника.
Нахождение
угла между прямой и плоскостью.Нахождение расстояния между прямой и плоскостью.
Слайд 24Группа 1.
В прямоугольном параллелепипеде ABCDA1B1C1D1 AB=2, AD=AA1=1.
Найдите угол между прямой A1B1 и плоскостью AB1D1.
Ответ: arcsin
.
Слайд 25Группа 2.
В правильной треугольной призме ABCA1B1C1 стороны основания равны 1, боковые
рёбра равны 3, точка D – середина ребра CC1. Найдите угол между
плоскостями ABC и ADB1.Ответ: arctg3.
Слайд 26Группа 3.
В правильной четырёхугольной призме ABCDA1B1C1D1 стороны основания равны 1, а
боковые рёбра равны 4. На ребре AA1 отмечена точка E так, что
AE:EA1=3:1. Найдите угол между плоскостями ABC и BED1.Ответ: arctg
.
Слайд 27Группа 4.
В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны
4, а боковые рёбра равны 8. Найдите площадь сечения пирамиды
плоскостью, проходящей через точку B и середину ребра MD параллельно прямой AC.Ответ:
.
Слайд 28Группа 5.
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания равна 22, а
боковое ребро AA1=7. Точка K принадлежит ребру B1C1 и делит его в
отношении 6:5, считая от вершины B1. Найдите площадь сечения этой призмы плоскостью, проходящей через точки B, D и K.Ответ: 176
.
Слайд 29Группа 6.
В прямоугольном параллелепипеде ABCDA1B1C1D1 известны рёбра AB=4, AD=3, AA1=7. Точка
O принадлежит ребру BB1 и делит его в отношении 3:4, считая от
вершины B. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки A, O и C1.Ответ: