Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Вычисление площадей геометрических фигур
Содержание
- 1. Вычисление площадей геометрических фигур
- 2. АПараллелограммАВСДКПараллелограмм-это четырёхугольник, у которого противолежащие стороны параллельны.ВК
- 3. аРомбааd1d2Ромб – это параллелограмм, у которого все
- 4. аПрямоугольникаbПрямоугольник – это параллелограмм, у которого все углы прямые.Площадь прямоугольника: S = a · b
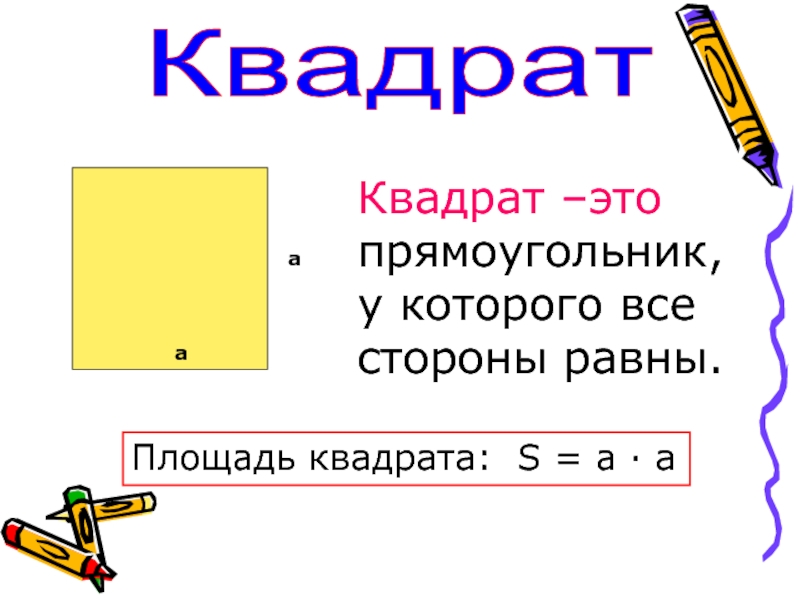
- 5. КвадратаaКвадрат –это прямоугольник,у которого все стороны равны.Площадь квадрата: S = a · a
- 6. Трапеция – это четырёхугольник, у которого две
- 7. АТреугольникАВСКТреугольник – это фигура, состоящая из трёх
- 8. АПрямоугольный треугольникАВСПрямоугольный треугольник – это треугольник,
- 9. АРавнобедренный треугольникАВСКРавнобедренный треугольник –это треугольник, у
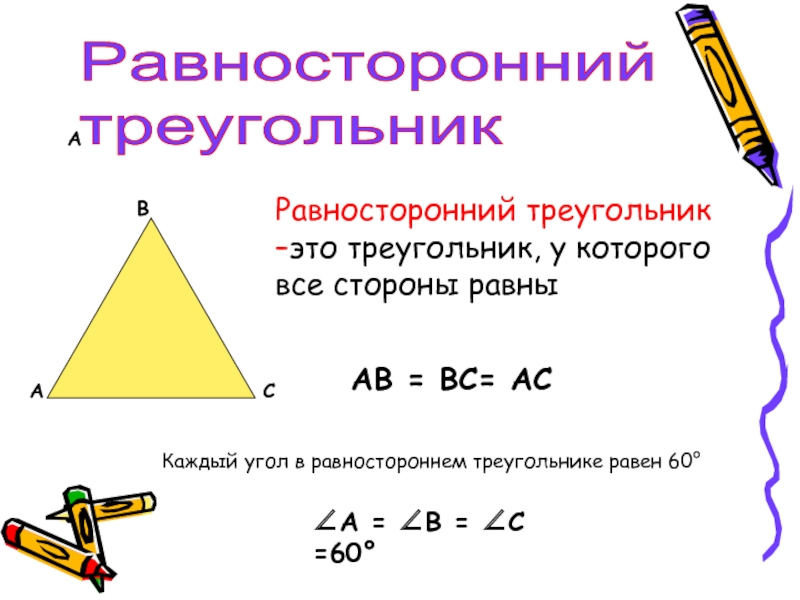
- 10. АРавносторонний треугольникАВСРавносторонний треугольник –это треугольник, у
- 11. Скачать презентанцию
АПараллелограммАВСДКПараллелограмм-это четырёхугольник, у которого противолежащие стороны параллельны.ВК – высота (перпендикулярна АД)Площадь параллелограмма: S = АД · ВКСумма углов четырёхугольника равна 360°
Слайды и текст этой презентации
Слайд 1Повторение свойств и вычисление площадей геометрических фигур.
Тема урока:
Повторение свойств
и вычисление площадей геометрических фигур.
Слайд 2А
Параллелограмм
А
В
С
Д
К
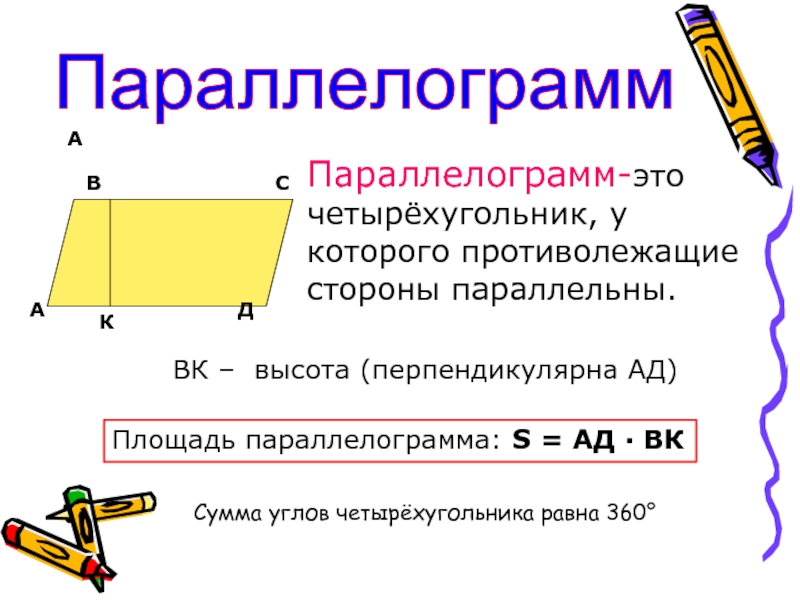
Параллелограмм-это четырёхугольник, у которого противолежащие стороны параллельны.
ВК – высота (перпендикулярна
АД)
Площадь параллелограмма: S = АД · ВК
Сумма углов четырёхугольника равна
360°
Слайд 3а
Ромб
а
а
d1
d2
Ромб – это параллелограмм, у которого все стороны равны
d1, d2
– диагонали ромба
Площадь ромба: S = ½ d1·d2
Слайд 4а
Прямоугольник
а
b
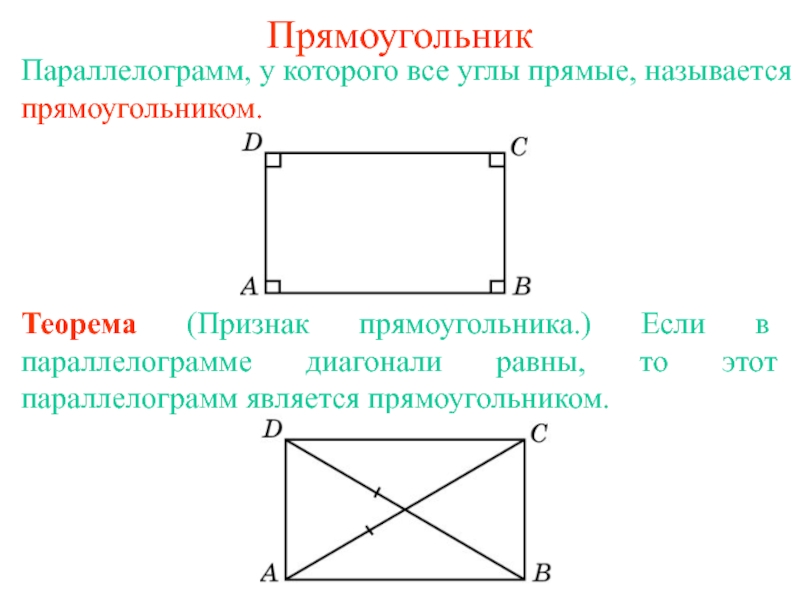
Прямоугольник – это параллелограмм, у которого все углы прямые.
Площадь прямоугольника:
S = a · b
Слайд 6Трапеция – это четырёхугольник, у которого две противолежащие стороны параллельны,
а две другие нет.
Трапеция
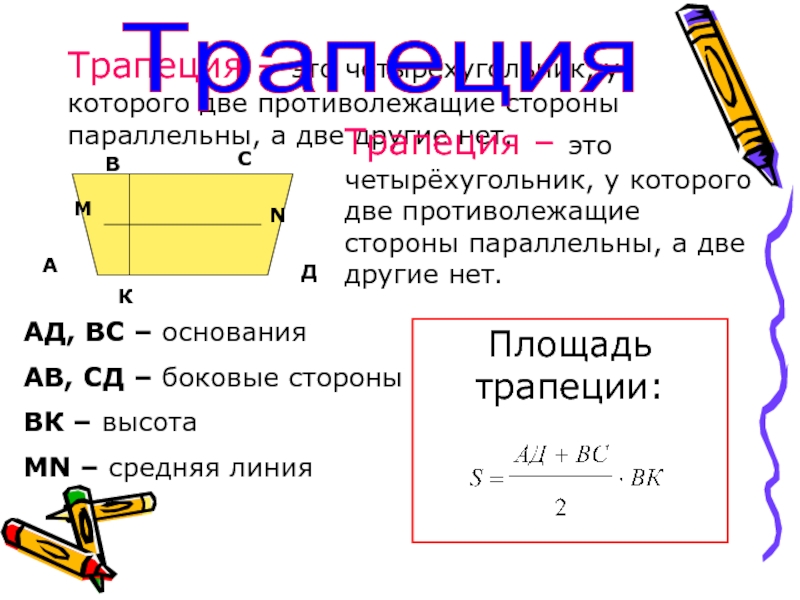
Трапеция – это четырёхугольник, у которого две
противолежащие стороны параллельны, а две другие нет.АД, ВС – основания
АВ, СД – боковые стороны
ВК – высота
MN – средняя линия
А
В
С
Д
К
M
N
Площадь трапеции:
Слайд 7А
Треугольник
А
В
С
К
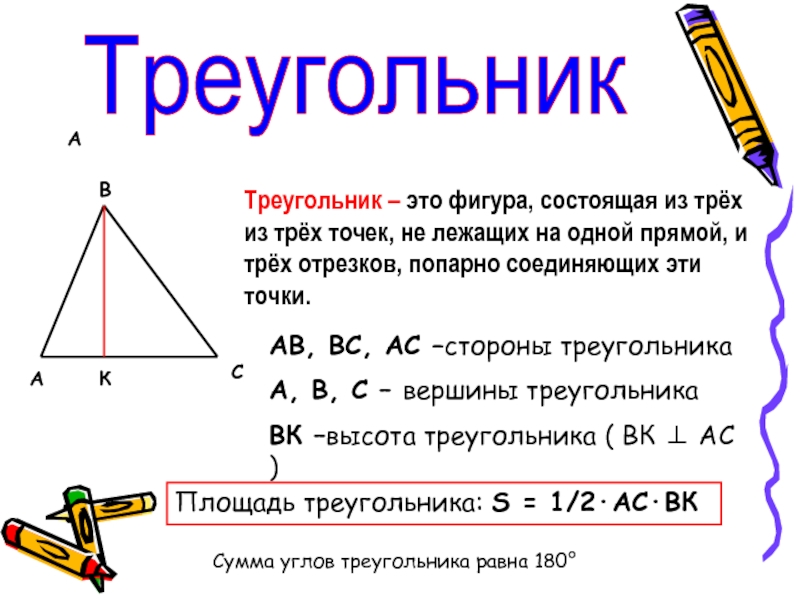
Треугольник – это фигура, состоящая из трёх из трёх точек,
не лежащих на одной прямой, и трёх отрезков, попарно соединяющих
эти точки.АВ, ВС, АС –стороны треугольника
А, В, С – вершины треугольника
ВК –высота треугольника ( ВК ⊥ АС )
Площадь треугольника: S = 1/2·АС·ВК
Сумма углов треугольника равна 180°
Слайд 8А
Прямоугольный
треугольник
А
В
С
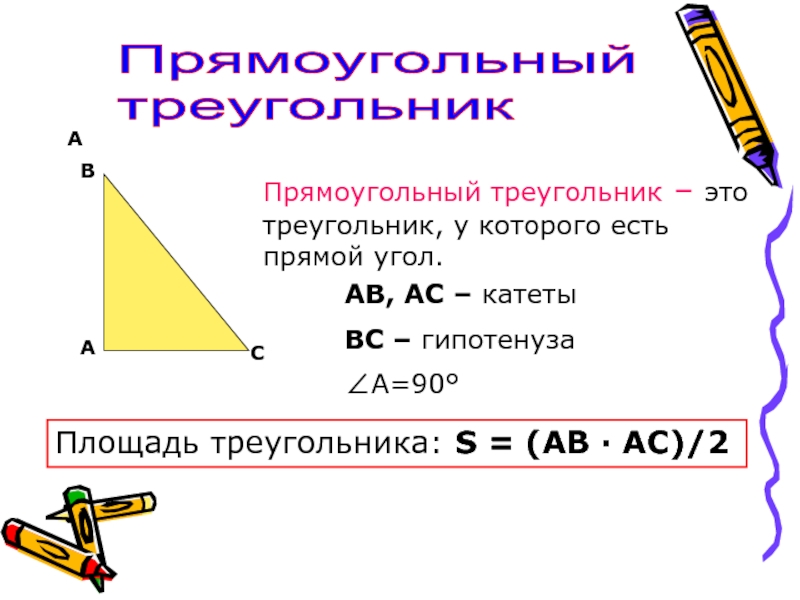
Прямоугольный треугольник – это треугольник, у которого есть прямой
угол.
АВ, АС – катеты
ВС – гипотенуза
∠А=90°
Площадь треугольника: S = (АВ
· АС)/2
Слайд 9А
Равнобедренный
треугольник
А
В
С
К
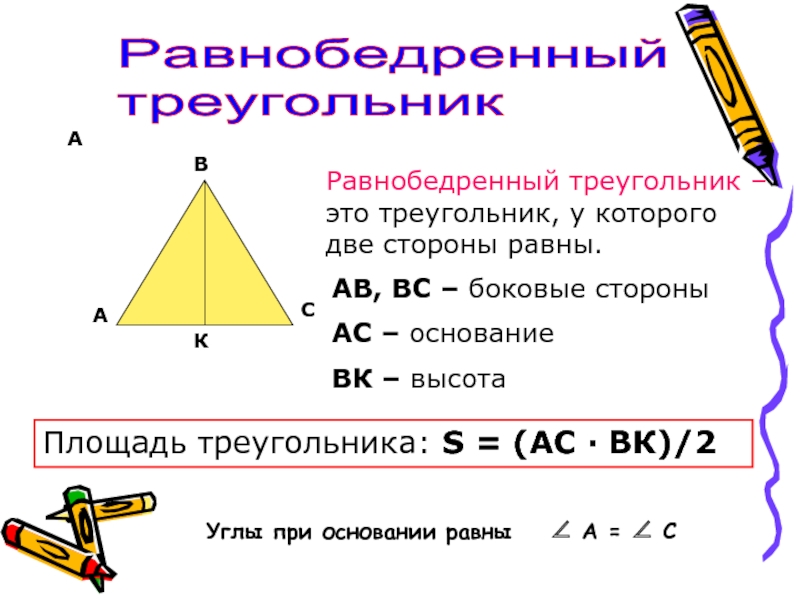
Равнобедренный треугольник –это треугольник, у которого две стороны равны.
АВ,
ВС – боковые стороны
АС – основание
ВК – высота
Площадь треугольника: S
= (АС · ВК)/2Углы при основании равны ∠ А = ∠ С
Слайд 10А
Равносторонний
треугольник
А
В
С
Равносторонний треугольник –это треугольник, у которого все стороны равны
АВ
= ВС= АС
Каждый угол в равностороннем треугольнике равен 60°
∠А =
∠В = ∠С =60°
Теги
