Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгебра логики Логические операции
Содержание
- 1. Алгебра логики Логические операции
- 2. ЛогикаЛогика – это наука о формах и
- 3. Алгебра логикиАлгебра логики — это математический аппарат,
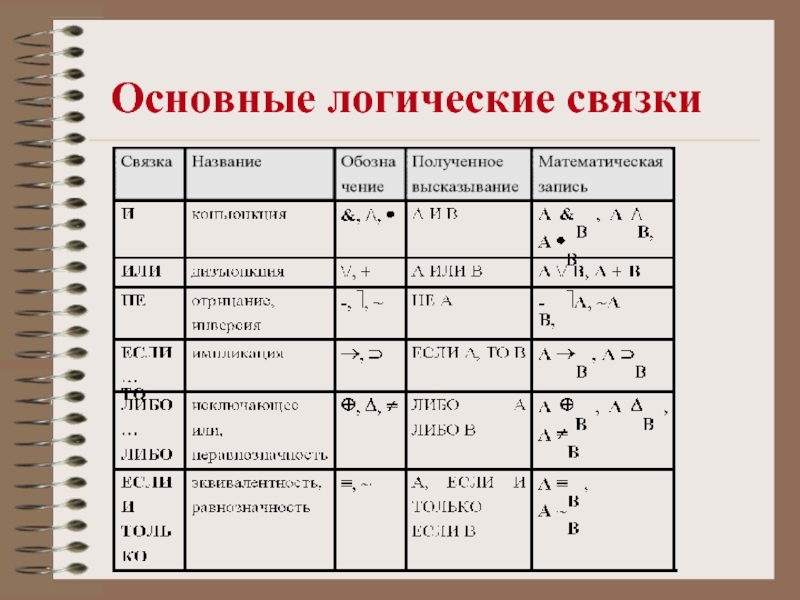
- 4. Основные логические связки
- 5. Таблица истинностиТаблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
- 6. Таблица истинностиДля формулы, которая содержит две переменные,
- 7. Основные логические операцииКОНЪЮНКЦИЯСоответствует союзу И;Обозначение &;В языках программирования and;Название: Логическое умножение.
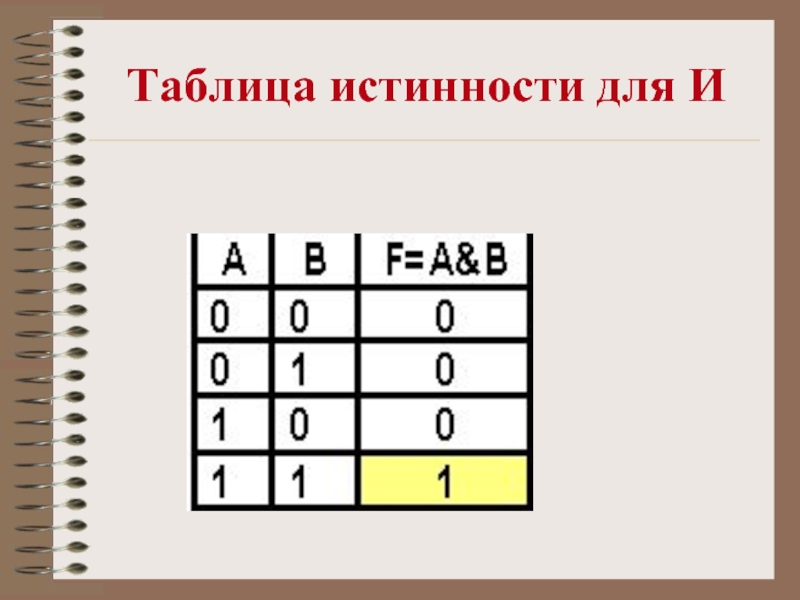
- 8. Таблица истинности для И
- 9. Основные логические операцииДИЗЪЮНКЦИЯСоответствует союзу ИЛИ;Обозначение V;В языках программирования or;Название: Логическое сложение.
- 10. Таблица истинности для ИЛИ
- 11. Основные логические операцииИНВЕРСИЯСоответствует союзу НЕ;Обозначение А;В языках программирования not;Название: Отрицание.
- 12. Таблица истинности для НЕ
- 13. Таблица истинности для эквивалентности
- 14. Порядок выполнения логических операций Порядок выполнения логических
- 15. Логическая формула Определение логической формулы: Всякая логическая
- 16. Тавтология Некоторые формулы принимают значение “истина” при
- 17. Тождественная истина При всех наборах значений
- 18. Тождественная ложь В качестве другого примера
- 19. Тождественная ложь При всех наборах значений
- 20. Выполнимая формулаФормула в некоторых случаях принимает значение
- 21. Основные законы алгебры логики Позволяют производить тождественные преобразования логических выражений:
- 22. Скачать презентанцию
ЛогикаЛогика – это наука о формах и законах человеческой мысли, о законах доказательных рассуждений, изучающая методы доказательств и опровержений, т.е. методы установления истинности или ложности одних высказываний (утверждений) на основе истинности
Слайды и текст этой презентации
Слайд 3Алгебра логики
Алгебра логики — это математический аппарат, с помощью которого
записывают, вычисляют, упрощают и преобразовывают логические высказывания.
Создателем алгебры логики
является живший в ХIХ веке английский математик Джордж Буль, в честь которого эта алгебра названа булевой алгеброй высказываний. Слайд 5Таблица истинности
Таблица истинности логической формулы выражает соответствие между всевозможными наборами
значений переменных и значениями формулы.
Слайд 6Таблица истинности
Для формулы, которая содержит две переменные, таких наборов значений
переменных всего четыре: (0,0), (0,1), (1,0), (1,1).
Если формула содержит три
переменные, то возможных наборов значений переменных восемь:(0,0,0), (0,0,1), (0,1,0), (0,1,1),
(1,0,0), (1,0,1), (1,1,0), (1,1,1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Слайд 7Основные логические операции
КОНЪЮНКЦИЯ
Соответствует союзу И;
Обозначение &;
В языках программирования and;
Название: Логическое
умножение.
Слайд 9
Основные логические операции
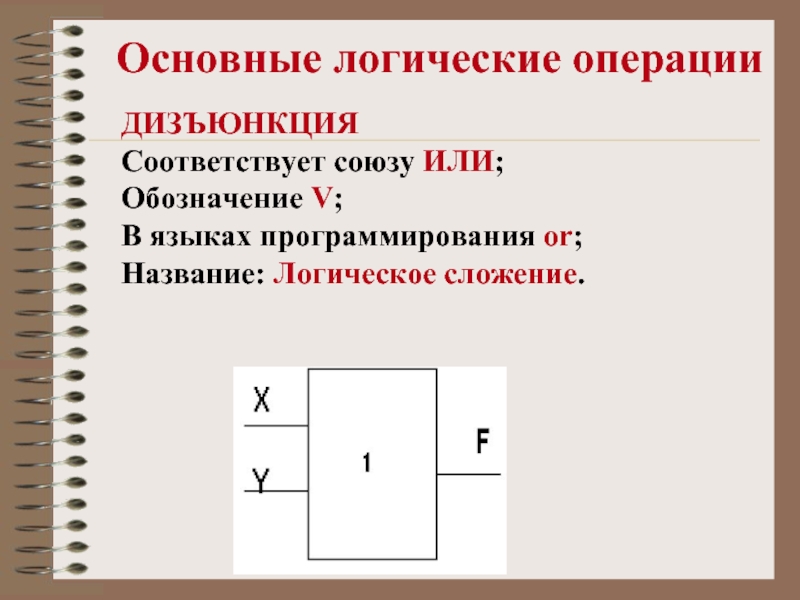
ДИЗЪЮНКЦИЯ
Соответствует союзу ИЛИ;
Обозначение V;
В языках программирования or;
Название:
Логическое сложение.
Слайд 11
Основные логические операции
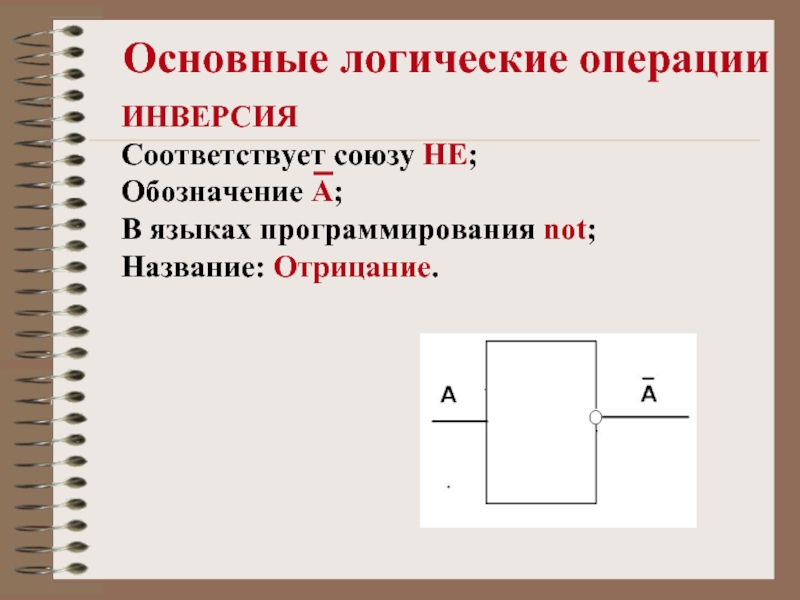
ИНВЕРСИЯ
Соответствует союзу НЕ;
Обозначение А;
В языках
программирования not;
Название: Отрицание.
Слайд 14Порядок выполнения логических операций
Порядок выполнения логических операций задается круглыми
скобками.
Но для уменьшения числа скобок договорились считать, что сначала
выполняется операция отрицания (“не”), затем конъюнкция (“и”), после конъюнкции — дизъюнкция (“или”) и в последнюю очередь — импликация →. Слайд 15Логическая формула
Определение логической формулы:
Всякая логическая переменная и символы
“истина” (“1”) и “ложь” (“0”) — формулы.
Если А и
В — формулы, то , (А • В), (А v В), (А → B), (А ↔ В) — формулы.
Слайд 16Тавтология
Некоторые формулы принимают значение “истина” при любых значениях истинности
входящих в них переменных. Например, формула А v
Такие формулы называются
тождественно истинными формулами или тавтологиями. Высказывания, которые формализуются тавтологиями, называются логически истинными высказываниями.
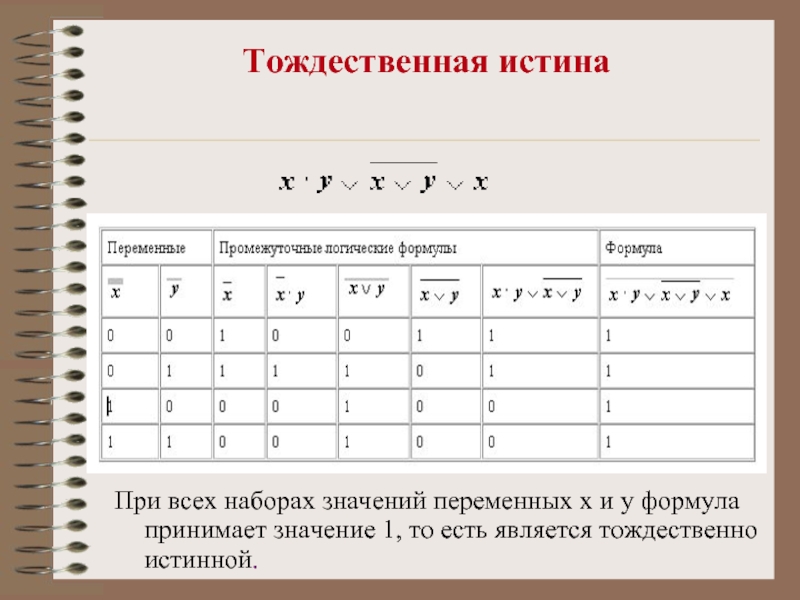
Слайд 17Тождественная истина
При всех наборах значений переменных x и y
формула принимает значение 1, то есть является тождественно истинной.
Слайд 18Тождественная ложь
В качестве другого примера рассмотрим формулу А •
, которой соответствует, например, высказывание “Катя самая высокая
девочка в классе, и в классе есть девочки выше Кати”. Очевидно, что эта формула ложна, так как либо А, либо обязательно ложно.Такие формулы называются тождественно ложными формулами или противоречиями.
Высказывания, которые формализуются противоречиями, называются логически ложными высказываниями.
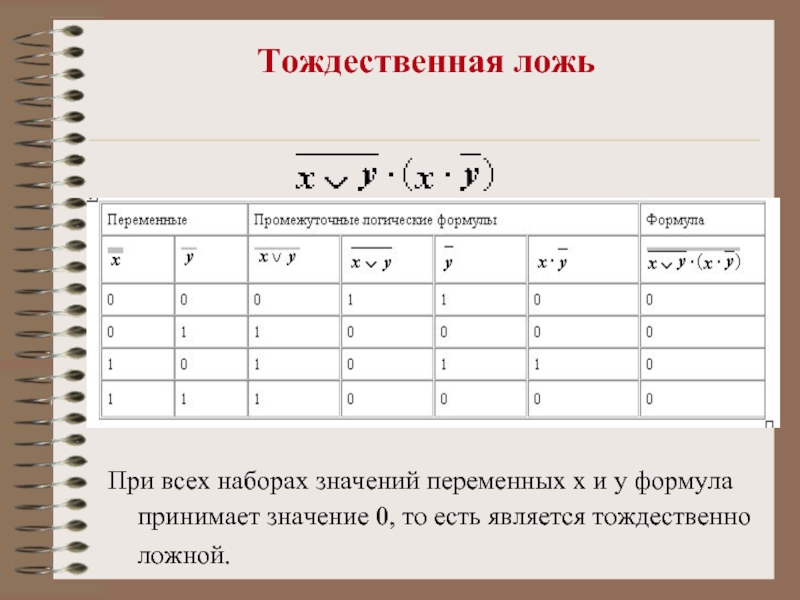
Слайд 19Тождественная ложь
При всех наборах значений переменных x и y
формула принимает значение 0, то есть является тождественно ложной.
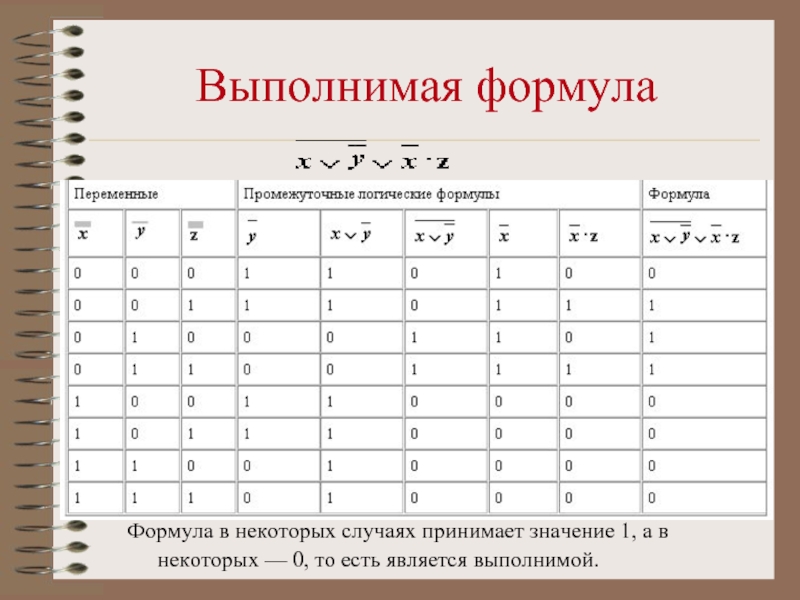
Слайд 20Выполнимая формула
Формула в некоторых случаях принимает значение 1, а в
некоторых — 0, то есть является выполнимой.
Слайд 21Основные законы алгебры логики
Позволяют производить тождественные преобразования логических выражений:
Теги