Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Алгоритм построения орграфа Хаффмана (алгоритм сжатия) 11 класс
Содержание
- 1. Алгоритм построения орграфа Хаффмана (алгоритм сжатия) 11 класс
- 2. Давид Хаффман (1925-1999)
- 3. Закодируем предложение «НА_ДВОРЕ_ТРАВА,_НА_ТРАВЕ_ДРОВА» Вначале нужно подсчитать количество вхождений каждого символа в тексте.Создаем первый узел013
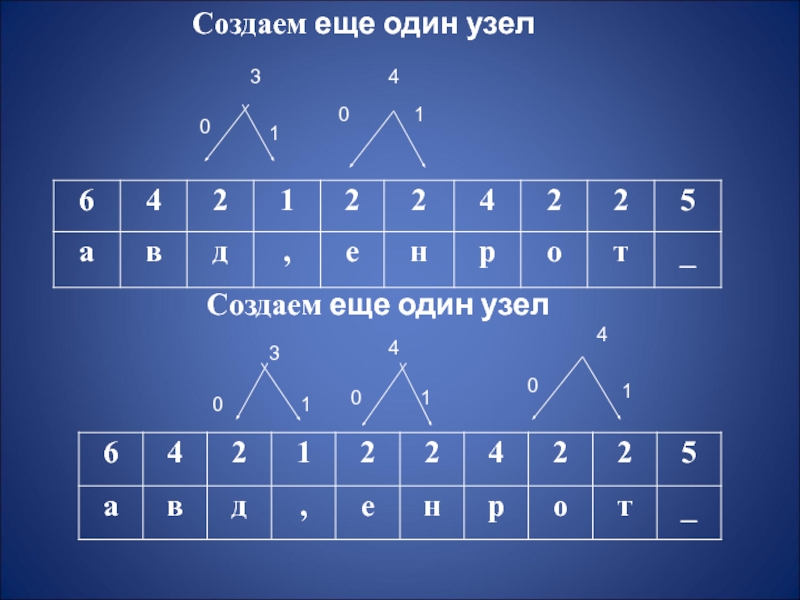
- 4. Создаем еще один узел11404001300114Создаем еще один узел3
- 5. Создаем еще один узел111004000171870000111144Создаем еще один узел
- 6. Создаем еще один узел111100000017189
- 7. Создаем еще один узел111100000001111389
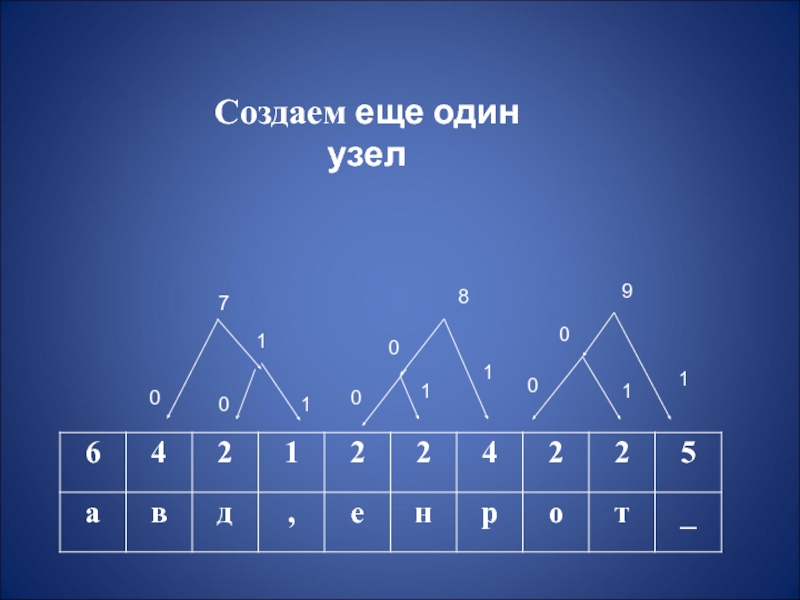
- 8. Создаем еще один узел11111000000001111317
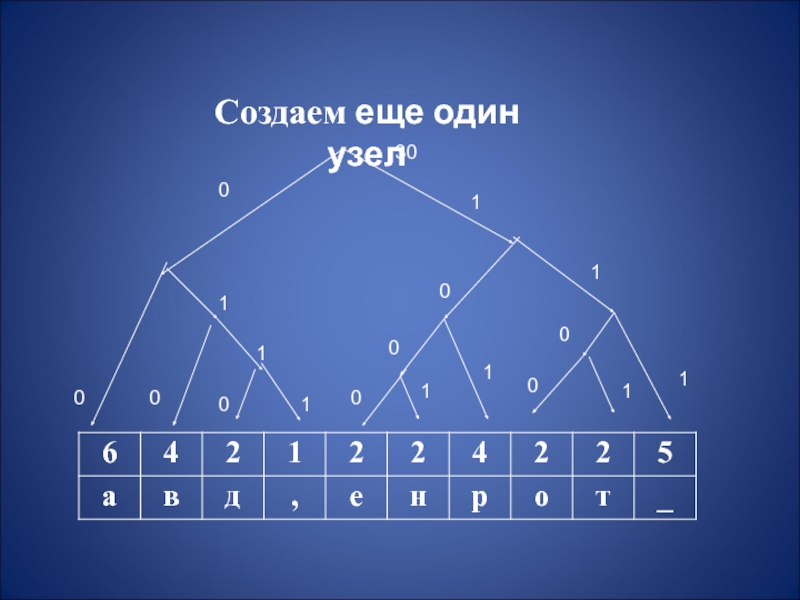
- 9. Создаем еще один узел30011111100000000111
- 10. Чтобы определить код для
- 11. ПОДСЧИТАЕМ, СКОЛЬКО ДВОИЧНЫХ СИМВОЛОВ
- 12. ПОСКОЛЬКУ В СООБЩЕНИИ ИСПОЛЬЗУЕТСЯ
- 13. НА САМОМ
- 14. ДЛЯ ДЕКОДИРОВНИЯ СЖАТОГО СООБЩЕНИЯ
- 15. Используемая литература:А.Г. Гейн. Математические основы информатики.Педагогический университет «Первое сентября», 2008г.http://edu.1september.ru/courses/07/008/01.pdf
- 16. Скачать презентанцию
Давид Хаффман (1925-1999) Давид начал свою научную карьеру студентом в Массачусетсом технологическом институте (MIT), где построил свои коды в начале пятидесятых годов прошлого века.
Слайды и текст этой презентации
Слайд 1Алгоритм построения орграфа Хаффмана
(алгоритм сжатия)
Учитель информатики:
Константинова Елена Ивановна
Муниципальное образовательное учреждение
Раменская средняя общеобразовательная школа №8
Слайд 2
Давид Хаффман (1925-1999)
Давид начал
свою научную карьеру студентом в Массачусетсом технологическом институте (MIT), где
построил свои коды в начале пятидесятых годов прошлого века.Слайд 3Закодируем предложение
«НА_ДВОРЕ_ТРАВА,_НА_ТРАВЕ_ДРОВА»
Вначале нужно подсчитать количество вхождений каждого символа в
тексте.
Создаем первый узел
0
1
3
Слайд 10 Чтобы определить код для каждого из символов,
входящих в сообщение, мы должны пройти путь от листа дерева,
соответствующего этому символу, до корня дерева, накапливая биты при перемещении по ветвям дерева. Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.Слайд 11
ПОДСЧИТАЕМ, СКОЛЬКО ДВОИЧНЫХ СИМВОЛОВ ОКАЖЕТСЯ В СООБЩЕНИИ
«НА_ ДВОРЕ_ ТРАВА,_ НА_ ТРАВЕ_ ДРОВА»
ДЛЯ
ЭТОГО НАДО НАЙТИ ПРОИЗВЕДЕНИЕ ЧИСЛА СИМВОЛОВ В КОДЕ КАЖДОЙ БУКВЫ НА КОЛИЧЕСТВО РАЗ, КОТОРОЕ ЭТА БУКВА ВСТРЕЧАЕТСЯ В СООБЩЕНИИ, А ЗАТЕМ ПОЛУЧЕННЫЕ ПРОИЗВЕДЕНИЯ СЛОЖИТЬ. ПОЛУЧАЕМ:2*6+ 3*4+ 4*2+ 4*1+ 4*2+ 4*2 +3*4 +4*2 +4*2 +3*5 = 95
Слайд 12
ПОСКОЛЬКУ В СООБЩЕНИИ ИСПОЛЬЗУЕТСЯ 10 РАЗЛИЧНЫХ СИМВОЛОВ,
ДЛЯ ИХ КОДИРОВАНИЯ ТРЕБУЕТСЯ КАК МИНИМУМ ЧЕТЫРЕХБИТОВЫЕ ЦЕПОЧКИ, ПОЭТОМУ ПОСЛЕ
КОДИРОВАНИЯ ДАННОГО СООБЩЕНИЯ ПОЛУЧИТСЯ ЦЕПОЧКА ОБЪЕМОМ 120 БИТ.КОЭФФИЦИЕНТ СЖАТИЯ ЭТО ОТНОШЕНИЕ ОБЪЕМА ИСХОДНОГО СООБЩЕНИЯ К ОБЪЕМУ СЖАТОГО. В НАШЕМ СЛУЧАЕ ЭТО ОТНОШЕНИЕ РАВНО 120/95 = 120/95 = 1,26 .
Слайд 13
НА САМОМ ДЕЛЕ ДАННОЕ СООБЩЕНИЕ
В ПАМЯТИ КОМПЬЮТЕРА ЗАКОДИРОВАНО С ПОМОЩЬЮ ASCII, ПОЭТОМУ НА КАЖДЫЙ
СИМВОЛ ОТВЕДЕНО 8 БИТ.ТЕМ САМЫМ, ОБЪЕМ ИСХОДНОГО СООБЩЕНИЯ 240 БИТ, А КОЭФФИЦИЕНТ СЖАТИЯ СОСТАВЛЯЕТ 240/95 = 2,53.
ИЗ ЭТОГО ВИДНО, КАКОЙ ВЫИГРЫШ МЫ ПОЛУЧИЛИ, ЕСЛИ ЭТО СООБЩЕНИЕ НУЖНО БЫЛО БЫ ПЕРЕДАТЬ ПО КАНАЛУ СВЯЗИ ИЛИ СОХРАНИТЬ НА КАКОМ-ЛИБО НОСИТЕЛЕ.
Слайд 14
ДЛЯ ДЕКОДИРОВНИЯ СЖАТОГО СООБЩЕНИЯ ВМЕСТЕ С НИМ
ОБЫЧНО ПЕРЕСЫЛАЮТ НЕ КОДЫ ИСХОДНЫХ СИМВОЛОВ (Т.Е. ПЕРВЫЕ ДВЕ СТРОКИ),
А САМ ОРГРАФ ХАФФМАНА (БЕЗ УКАЗАНИЯ ВЕСА КОРНЯ И РАЗМЕТКИ НА ДУГАХ, ИБО ОНА СТАНДАРТНА: ДУГА, ИДУЩАЯ ВЛЕВО, РАЗМЕЧАЕТСЯ -0, А ИДУЩАЯ ВПРАВО -1).НА ЭТОМ, ОКАЗЫВАЕТСЯ, ТО ЖЕ МОЖНО СЭКОНОМИТЬ.
МАТЕМАТИКИ ДОКАЗАЛИ, ЧТО СРЕДИ АЛГОРИТМОВ КОДИРУЮЩИХ КАЖДЫЙ СИМВОЛ ПО ОТДЕЛЬНОСТИ И ЦЕЛЫМ КОЛИЧЕСТВОМ БИТ АЛГОРИТМ ХАФФМАНА ОБЕСПЕЧИВАЕТ НАИЛУЧШЕЕ СЖАТИЕ.