Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Двоичная система счисления. Перевод целых десятичных чисел в двоичный код 6 класс
Содержание
- 1. Двоичная система счисления. Перевод целых десятичных чисел в двоичный код 6 класс
- 2. Вильгельм Готфрид Лейбниц (1646-1716)Медаль, нарисованная В. Лейбницем
- 3. 1 способ – метод разностей.Любое десятичное число
- 4. Переведем число 121 в двоичную систему счисления.121
- 5. 121=64+32+16+8+1==1.64+1.32+1.16+1.8++0.4+0.2+1.1
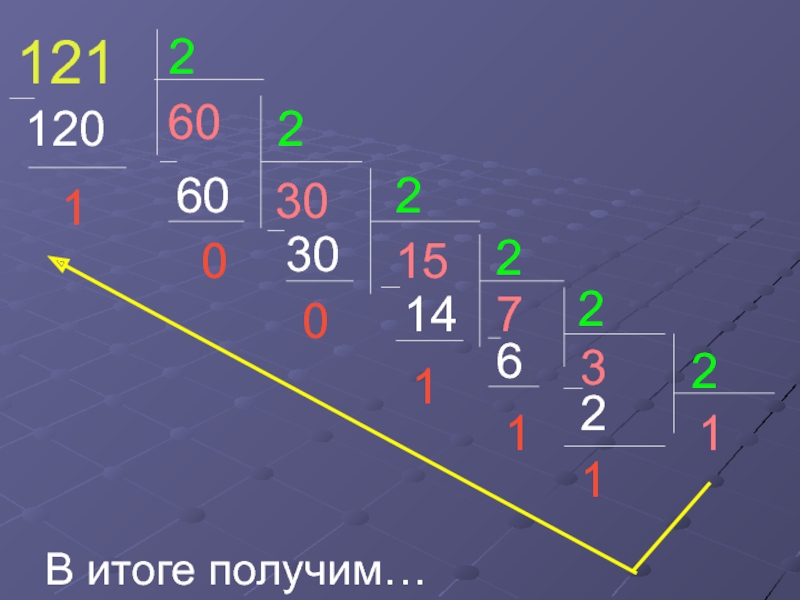
- 6. 2 способ.Выполняем деление десятичного числа и получаемых
- 7. 12126012012306002301502714123611221В итоге получим…
- 8. Слайд 8
- 9. Время в двоичной системе счисления
- 10. С виду двоичные часы напоминают совершенно обычную
- 11. часы: (1010) = 10 минуты:четверть: I
- 12. Скачать презентанцию
Вильгельм Готфрид Лейбниц (1646-1716)Медаль, нарисованная В. Лейбницем в 1697 г., поясняющая соотношение между двоичной и десятичной системами исчисления
Слайды и текст этой презентации
Слайд 1Двоичная система счисления
Перевод целых десятичных чисел в двоичный код.
Автор: Загоскина
Н.С.,
Слайд 2Вильгельм Готфрид Лейбниц
(1646-1716)
Медаль, нарисованная В. Лейбницем в 1697 г., поясняющая
соотношение между двоичной и десятичной системами исчисления
Слайд 31 способ – метод разностей.
Любое десятичное число можно представить в
виде суммы слагаемых ряда:
1, 2, 4, 8, 16, 32, 64,
128,...Слайд 4Переведем число 121 в двоичную систему счисления.
121 – 64 =
57
57 – 32 = 25
25 – 16 = 9
9 –
8 = 1В итоге получим…
Слайд 62 способ.
Выполняем деление десятичного числа и получаемых неполных частных на
основание двоичной системы – 2 до тех пор, пока не
получим неполное частное меньшее делителя (2).Слайд 10С виду двоичные часы напоминают совершенно обычную китайскую поделку, однако,
если нажать на кнопку, которая находится у них на боку,
то нормальное время сразу же переведется в двоичный форматСлайд 11часы: (1010) = 10
минуты:
четверть: I (00) = 0; II (01)
= 16; III (10)=32; IV (11) = 48;
плюс еще значение
(1001) = 9;
итого: (011001) = 16 + 9 = 25.Время 10:25.