Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формы мышления. Алгебра высказываний
Содержание
- 1. Формы мышления. Алгебра высказываний
- 2. Цель: Рассмотреть основные понятия логики предикатов.
- 3. Логика – это наука о формах и
- 4. Понятие. Понятие – это форма мышления,
- 5. Алгебра множеств, одна из основополагающих
- 6. Для наглядной иллюстрации объемов
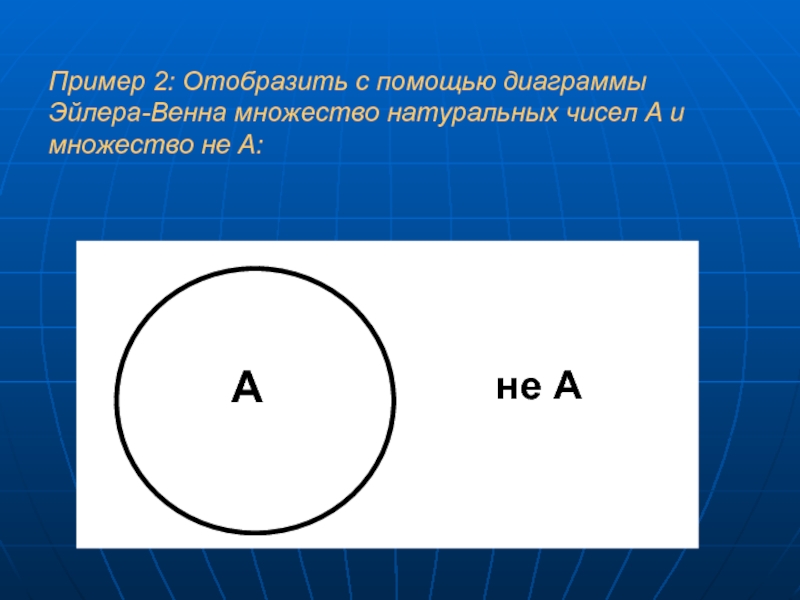
- 7. Ане АПример 2: Отобразить с помощью диаграммы Эйлера-Венна множество натуральных чисел А и множество не А:
- 8. Высказывание – это предложение в
- 9. Общее высказывание начинается со слов:
- 10. Частное высказывание начинается со слов:
- 11. Во всех других случаях высказывание является единичным.
- 12. Высказывание может быть простым или составным.
- 13. Высказывания имеют определенную логическую форму.
- 14. Оба эти понятия – субъект и
- 15. Пример: Иванов является учеником 10 б. Здесь
- 16. Умозаключение. Умозаключение – это форма
- 17. В дедуктивных умозаключениях рассуждения ведутся
- 18. В индуктивных умозаключениях рассуждения ведутся
- 19. Умозаключение по аналогии представляет собой
- 20. Доказательство. Доказательство – есть мыслительный процесс,
- 21. Спасибоза внимание!
- 22. Автор презентации:Ширяева Ольга Мухадинновна,Муниципальное Общеобразовательное Учреждение«Средняя общеобразовательная школа №2»,учитель информатики,1 квалификационной категории.http://www.shiryaeva.86sch2-nyagan.edusite.ru
- 23. В презентации использованыматериалы учебного пособия: «ПРАКТИКУМ по
- 24. Скачать презентанцию
Цель: Рассмотреть основные понятия логики предикатов.
Слайды и текст этой презентации
Слайд 4Понятие.
Понятие – это форма мышления, отражающая наиболее существенные
свойства предмета, отличающие его от других предметов.
В
структуре каждого понятия нужно различать две стороны: содержание и объем. Содержание понятия составляет совокупность существенных признаков предмета.
Объем понятия определяется совокупностью предметов, на которую оно распространяется, и может быть представлено в форме множества объектов, состоящего из элементов множеств.
Слайд 5 Алгебра множеств, одна из основополагающих современных математических теорий.
Между множествами может могут быть различные виды отношений:
равнозначность,
когда объемы понятий полностью совпадаютпересечение, когда объемы понятий частично совпадают
подчинение, когда объем одного понятия полностью входит в объем другого.
Слайд 6 Для наглядной иллюстрации объемов понятий используются диаграммы
Эйлера-Венна. Если имеются какие-либо понятия А, В, С, то объем
каждого понятия (множество) можно представить в виде круга, а отношения между ними в виде пересекающихся кругов.Пример 1: Отобразить с помощью диаграммы Эйлера-Венна соотношение между объемами понятий натуральные числа и четные числа.
Натуральные числа – это множество целых положительных чисел А, а четные – это множество отрицательных и положительных чисел B. Там, где они пересекаются получается множество натуральных четных чисел С:
Слайд 7
А
не А
Пример 2: Отобразить с помощью диаграммы Эйлера-Венна множество натуральных
чисел А и множество не А:
Слайд 8 Высказывание – это предложение в отношении которого можно
однозначно сказать истинно оно или ложно. Высказывания бывают общими, частными
или единичными.Слайд 9 Общее высказывание начинается со слов: все, всякий, каждый,
ни один.
Все кошки умеют летать
Всякий ребенок ходит в школу
Ни
один ребенок не старше своей мамыКаждая рыба умеет плавать
Слайд 10 Частное высказывание начинается со слов: некоторые, большинство и
т.п.
Некоторые птицы умеют разговаривать
Большинство людей любят мороженное
Слайд 12 Высказывание может быть простым или составным.
Простое высказывание,
если никакая его часть сама не является высказыванием.
Составное
– это высказывание, состоящее из простых высказываний.Слайд 13 Высказывания имеют определенную логическую форму.
Понятие о
предмете мысли называется субъектом и обозначается буквой S, а понятие
о свойствах и отношениях предмета называется предикатом и обозначается буквой Р.Слайд 14 Оба эти понятия – субъект и предикат называются терминами
суждения.
Отношения между субъектом и предикатом выражаются связкой «есть», «не
есть», «является», «состоит» и т.д. Таким образом, каждое высказывание состоит из трех элементов – субъекта, предиката и связки.
Состав суждения можно выразить общей формулой «S есть Р» или «S не есть Р».
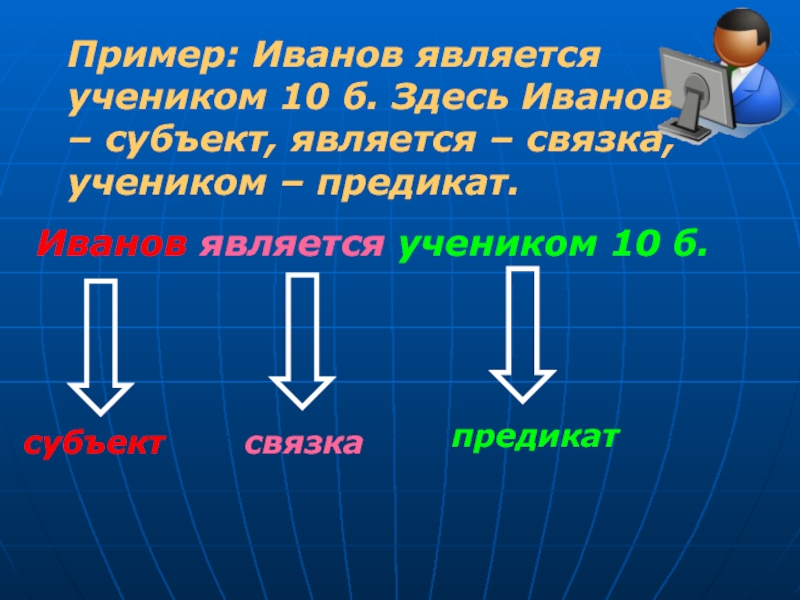
Слайд 15Пример: Иванов является учеником 10 б. Здесь Иванов – субъект,
является – связка, учеником – предикат.
Иванов является учеником 10 б.
субъект
связка
предикат
Слайд 16Умозаключение.
Умозаключение – это форма мышления, с помощью
которой из одного или нескольких суждений (посылок) может быть получено
новое суждение (вывод).Умозаключения бывают дедуктивные, индуктивные и по аналогии.
Слайд 17 В дедуктивных умозаключениях рассуждения ведутся от общего к
частному.
Например, из двух высказываний: «Ртуть является металлом»
и «Все металлы электропроводны» можно сделать вывод «Ртуть электропроводна».Слайд 18 В индуктивных умозаключениях рассуждения ведутся от частного к
общему.
Например, установив, что отдельные металлы – железо,
медь, цинк и так далее – обладают свойством электропроводности можно сделать вывод, что все металлы электропроводны.Слайд 19 Умозаключение по аналогии представляет собой движение мысли от
общности одних свойств и отношений у сравниваемых предметов или процессов.
Например, химический состав Солнца и Земли сходен по многим показателям, поэтому, когда на Солнце нашли еще неизвестный элемент гелий, предположили, что данный элемент есть и на Земле.
Слайд 20Доказательство.
Доказательство – есть мыслительный процесс, направленный на подтверждение
или опровержение какого либо положения посредством других несомненных, ранее обоснованных
доводов.Слайд 22Автор презентации:
Ширяева Ольга Мухадинновна,
Муниципальное Общеобразовательное Учреждение
«Средняя общеобразовательная школа №2»,
учитель информатики,
1
квалификационной категории.
http://www.shiryaeva.86sch2-nyagan.edusite.ru
Слайд 23В презентации использованы
материалы учебного пособия: «ПРАКТИКУМ по
информатике и информационным
технологиям», Н.
Угринович, Л. Босова,
Н. Михайлова - М.: БИНОМ. Лаборатория знаний,
2004.
Теги