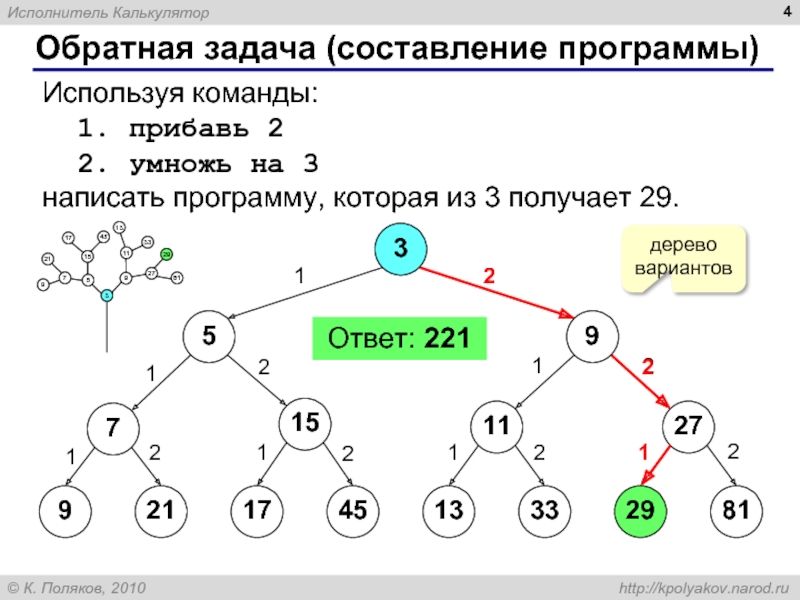
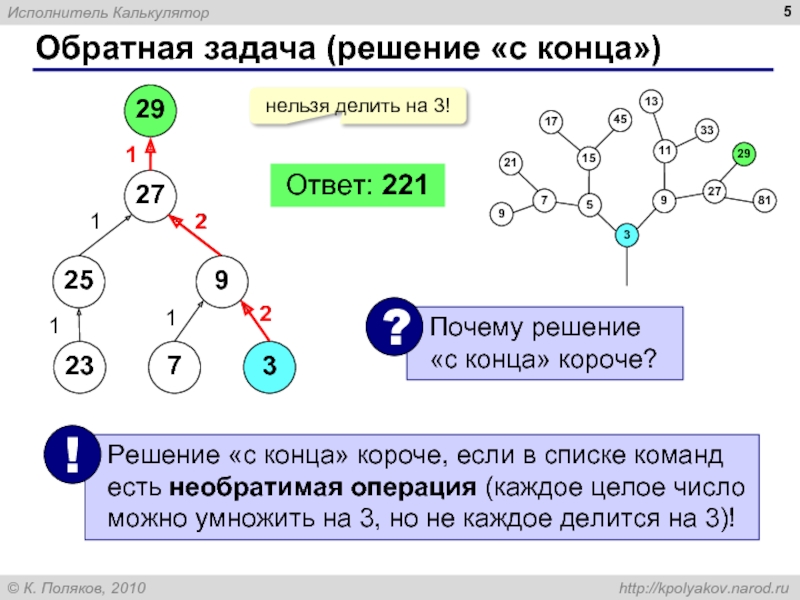
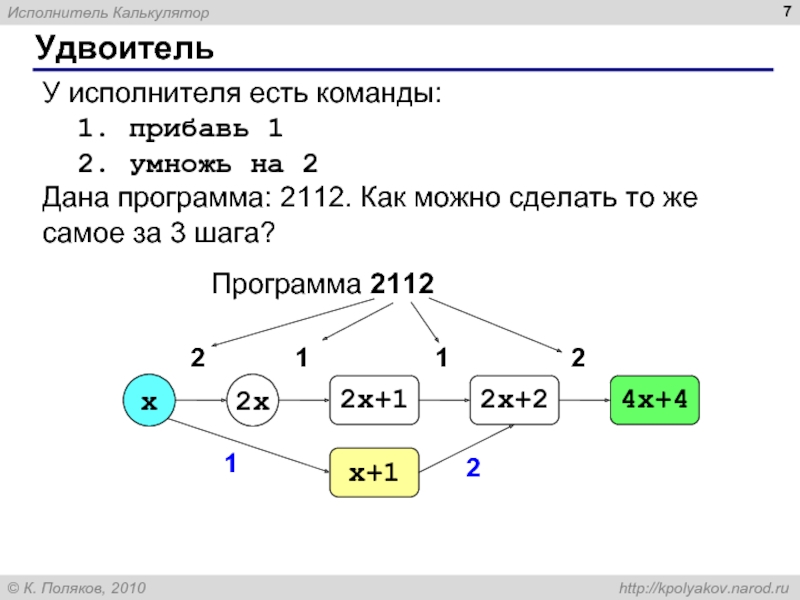
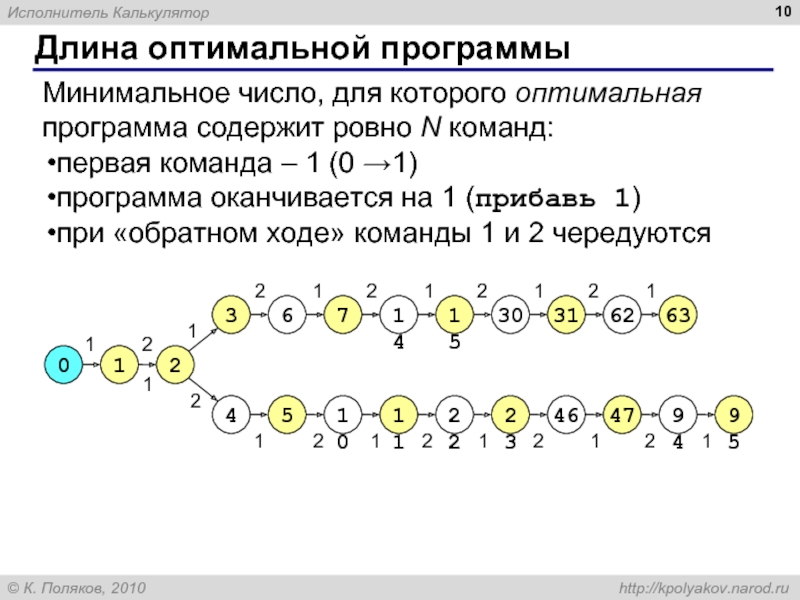
команды, известные исполнителю (входящие в СКИ)
определенность: при одинаковых исходных данных
всегда выдает один и тот же результатконечность: заканчивается за конечное число шагов
массовость: может применяться многократно при различных исходных данных
корректность: дает верное решение при любых допустимых исходных данных
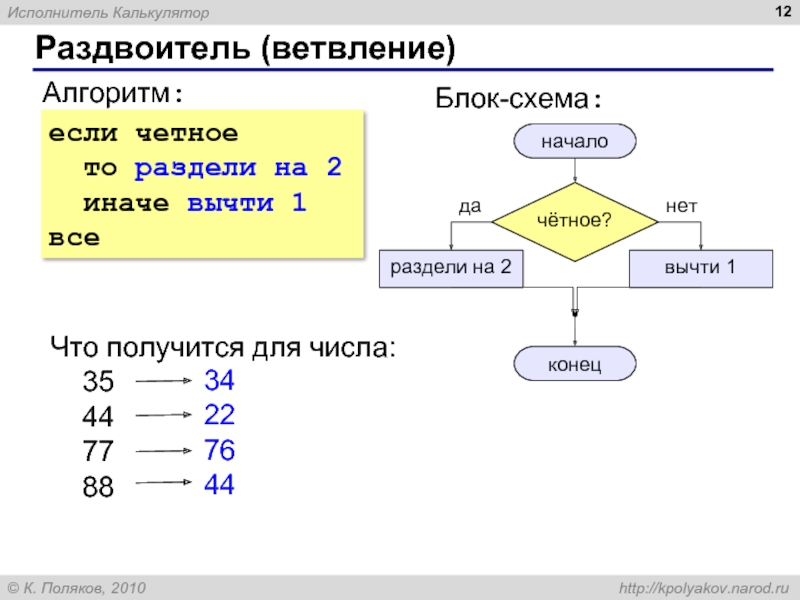
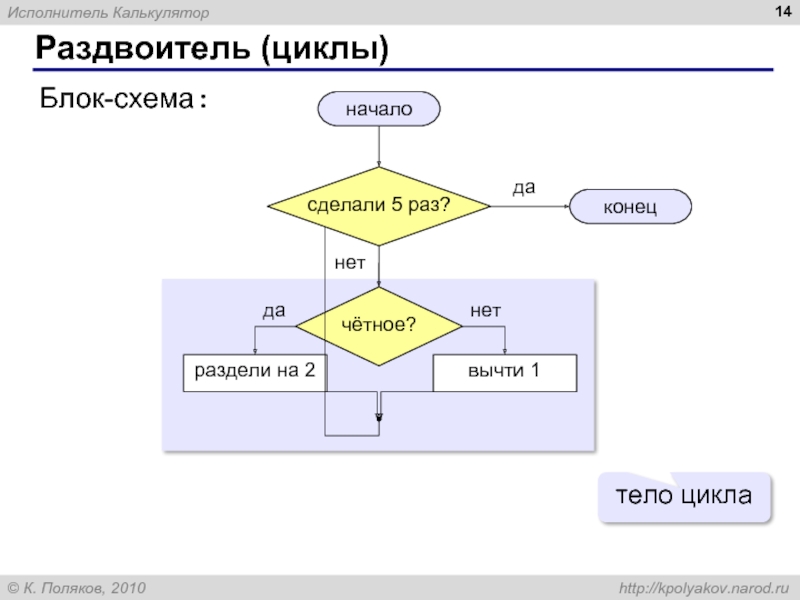
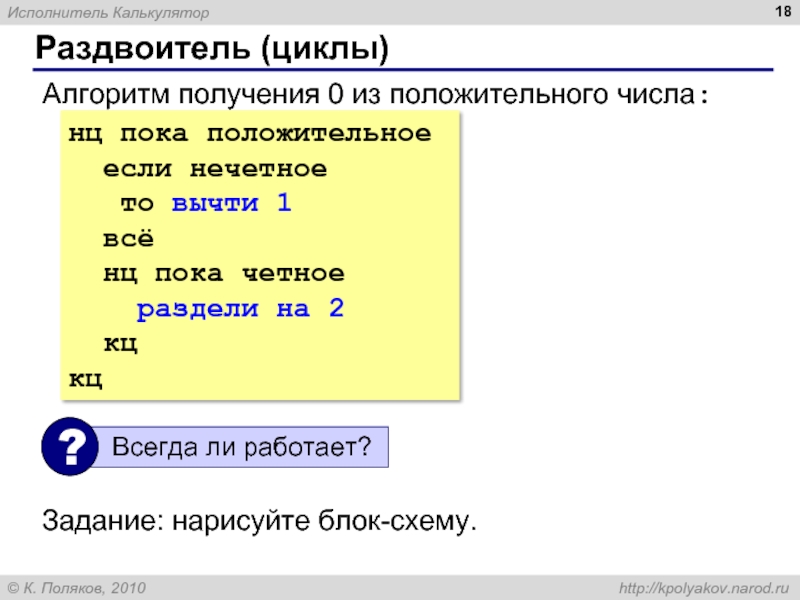
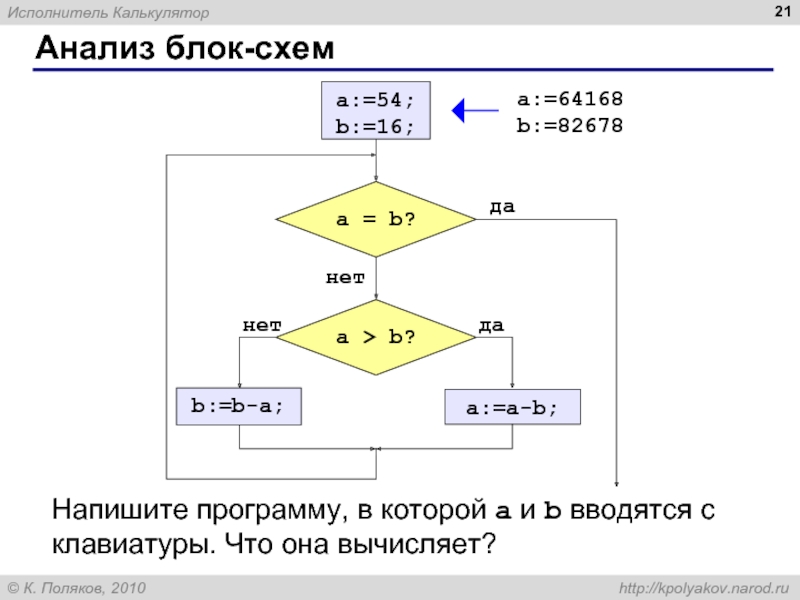
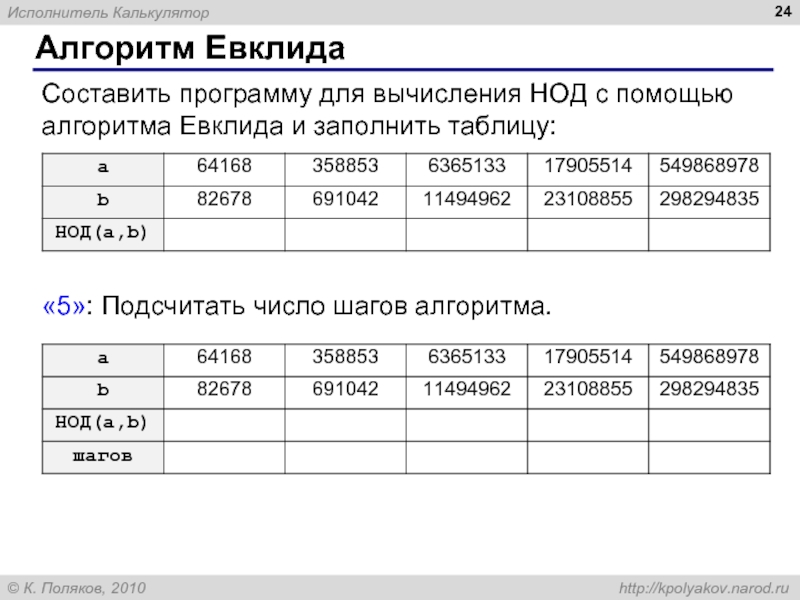
Алгоритм – это четко определенный план действий для исполнителя.