Слайд 1Исследование физических моделей
Построение и исследование модели на примере движения тела,
брошенного под углом к горизонту.
Биологические модели развития популяций
Оптимизационное моделирование в
экономике
Геоинформационные модели
Слайд 2Построение и исследование модели на примере движения тела, брошенного под
углом к горизонту.
Содержательная постановка задачи:
-в процессе тренировки теннисистов используют автоматы
по бросанию мячика в определенное место площадки. Необходимо задать автомату скорость и угол бросания мячика для попадания в мишень определенного размера, находящуюся на известном расстоянии.
Слайд 3Качественная описательная модель
Из условия задачи можно сформулировать основные предположения:
-мячик мал
по сравнению с Землей, поэтому его можно считать материальной точкой;
-изменение
высоты мячика мало, поэтому ускорение свободного падения можно считать постоянной величиной g=9,8 м/с2 и движение по оси OY можно считать равноускоренным;
-скорость бросания тела мала, поэтому сопротивлением воздуха можно пренебречь и движение по оси OX можно считать равномерным
Слайд 4Синус острого угла в прямоугольном треугольнике
— это отношение противолежащего катета к гипотенузе:
Косинус острого
угла в прямоугольном треугольнике —
отношение прилежащего катета к гипотенузе:
Тангенс острого угла в прямоугольном
треугольнике —
отношение противолежащего катета к прилежащему:
Слайд 5Формальная модель
Для формализации модели используем формулы равномерного и равноускоренного движения.
При заданных начальной скорости v0 и угле бросания α значения
координат дальности полета х и высоты у от времени можно описать следующими формулами:
Высоту мячика L над землей на расстоянии S определяем по формуле:
Попадание произойдет, если значение высоты L мячика будет удовлетворять неравенству:
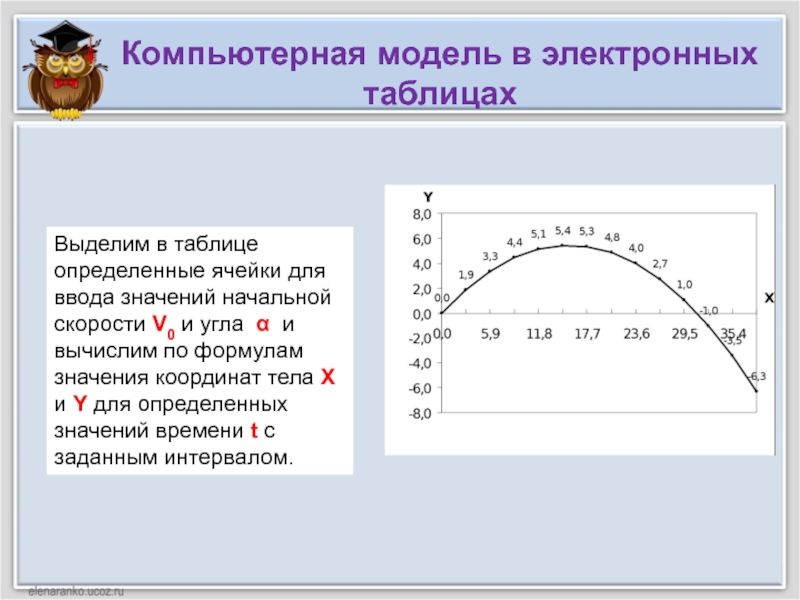
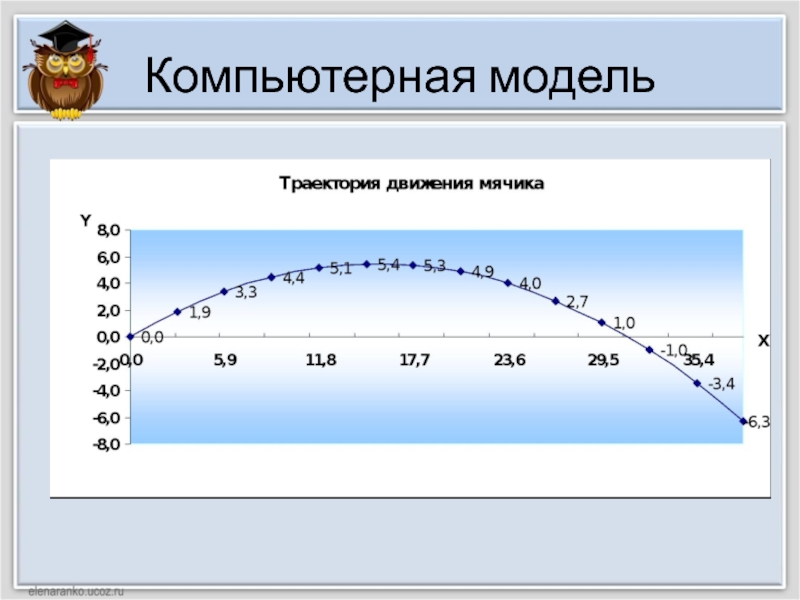
Слайд 6Компьютерная модель в электронных таблицах
Выделим в таблице определенные ячейки для
ввода значений начальной скорости V0 и угла α и вычислим
по формулам значения координат тела Х и Y для определенных значений времени t с заданным интервалом.
Слайд 7Задача «Бросание мячика в стенку»
I этап. Постановка задачи
Описание задачи:
В
процессе тренировок теннисистов используются автоматы по бросанию мячика. Необходимо задать
автомату нужную скорость и угол бросания мячика для попадания в стенку определённой высоты, находящуюся на известном расстоянии.
Слайд 8Цель моделирования
Определить скорость и угол бросания мячика для попадания в
стенку
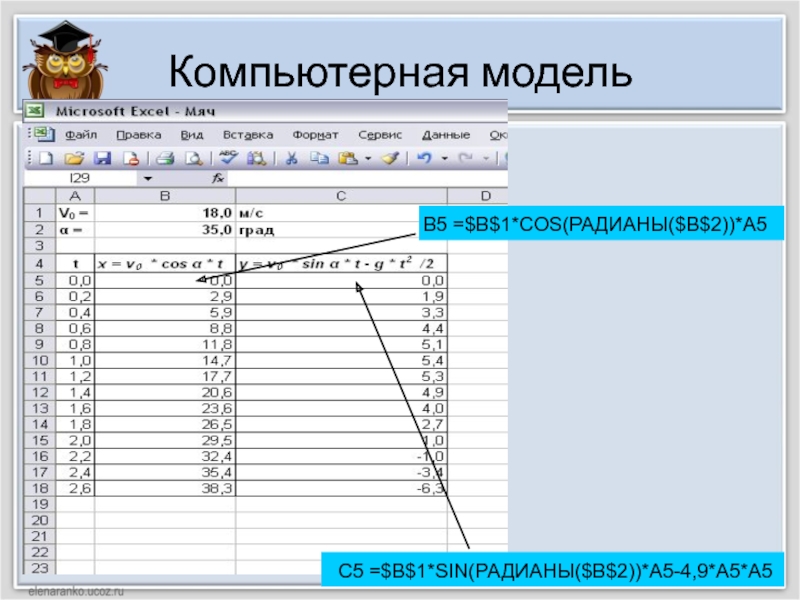
Слайд 9Компьютерная модель
С5 =$B$1*SIN(РАДИАНЫ($B$2))*A5-4,9*A5*A5
В5 =$B$1*COS(РАДИАНЫ($B$2))*A5
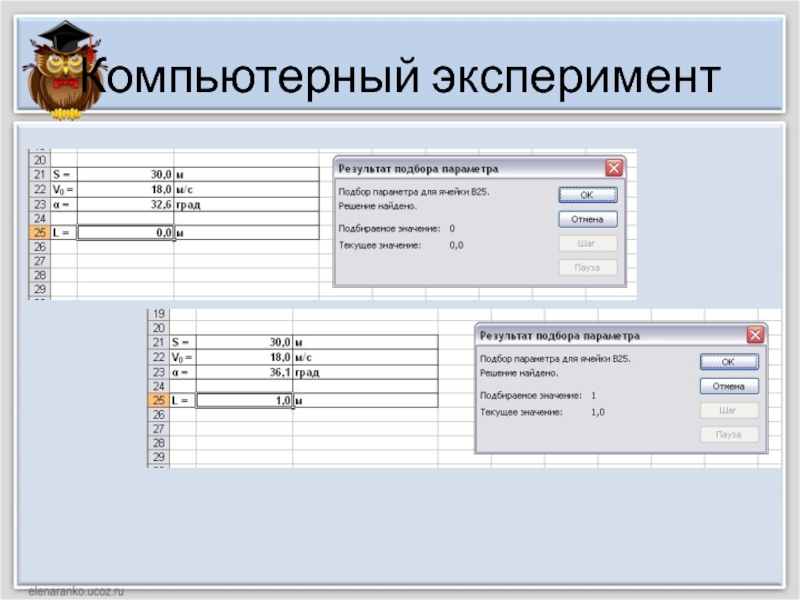
Слайд 11Компьютерный эксперимент
В25 = B21*TAN(РАДИАНЫ(B23))-(9,81*B21^2)/(2*B22^2*COS(РАДИАНЫ(B23))^2)
Слайд 14Исследование модели
Исследуем модель и определим с заданной точностью 0,1º диапазон
изменений угла, который обеспечивает попадание в мишень, находящуюся на расстоянии
30 м и имеющую высоту 1 м, при заданной начальной скорости 18 м/с.
Воспользуемся для этого методом Подбор параметров.
Выводы: Таким образом, исследование компьютерной модели в электронных таблицах показало, что существует диапазон значений угла бросания ( указать ! ) , который обеспечивает попадание в мишень высотой 1 м, находящуюся на расстоянии 30 м, мячиком, брошенным со скоростью 18 м/с.
Слайд 15Биологические модели развития популяций
Слайд 16 В биологии при исследовании развития развития биосистем
строятся динамические модели изменения численности популяций различных живых существ с
учетом различных факторов.
Взаимовлияние популяций рассматривается в моделях типа «хищник – жертва».
Формальная модель
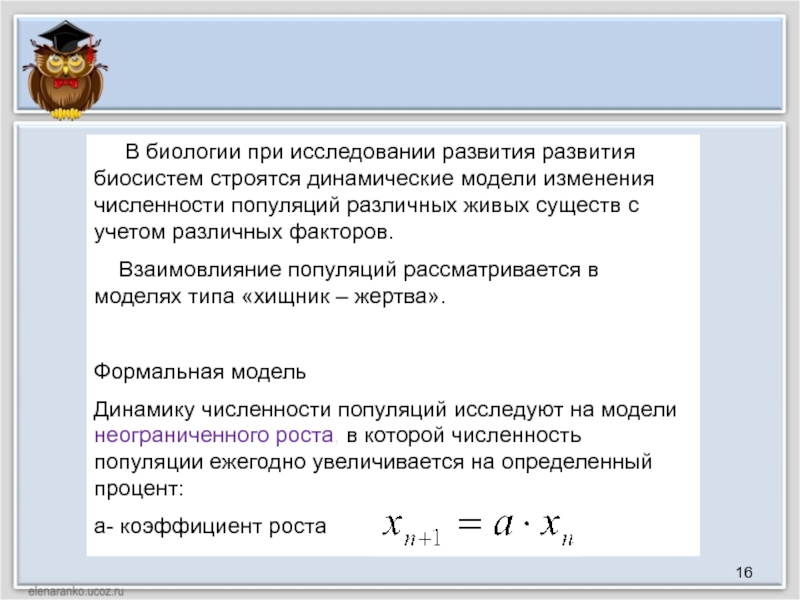
Динамику численности популяций исследуют на модели неограниченного роста, в которой численность популяции ежегодно увеличивается на определенный процент:
а- коэффициент роста
Слайд 17 В модели ограниченного роста учитывается коэффициент перенаселенности, связанный
с нехваткой питания, болезнями и т.д., который замедляет рост популяции
с увеличением ее численности:
b – коэффициент перенаселенности (b < a):
Слайд 18 В модели ограниченного роста с отловом учитывается,
что на численность популяции промысловых животных и рыб оказывает влияние
величина ежегодного
отлова – с:
В модели «хищник – жертва» количество жертв xn и количество хищников уn связаны между собой. Количество встреч жертв с хищниками можно считать пропорциональным произведению количеств жертв и хищников, а коэффициент f характеризует возможность гибели жертвы при встрече с хищниками:
Слайд 19Компьютерная модель
Построим в электронных таблицах компьютерную модель,
позволяющую исследовать численность популяций с использованием различных моделей: неограниченного роста,
ограниченного роста, ограниченного роста с отловом и «хищник – жертва».
A, b, c, f – значения коэффициентов, влияющих на изменение численности жертв
D, e - значения коэффициентов, влияющих на изменение численности хищников
Столбец D-численность популяции по модели неограниченного роста;
Столбец Е-численность популяции по модели ограниченного роста;
Столбец F- ограниченного роста c отловом;
Столбцы G и H -численность популяции по модели «хищник – жертва»
Слайд 20Исследование модели
Провести исследование моделей роста популяций различного типа, задавая различные
значения коэффициентов и начальные численности популяций. Подобрать значения коэффициентов, чтобы:
-
определить через сколько лет произойдет удвоение численности популяции в модели неограниченного роста;
численность популяций в моделях ограниченного роста и ограниченного роста с отловом стабилизировалась примерно на одном уровне (так определяют квоты на ловлю рыбы);
в модели «жертва – хищник» численность жертв и хищников стабилизировалась со временем (так определяют охотничьи квоты)
и сделать выводы.
Слайд 22 Геоинформационное моделирование базируется на создании многослойных
электронных карт, в которых опорный слой описывает географию определенной территории,
а каждый из остальных – один из аспектов состояния этой территории. На географическую карту могут быть выведены различные слои объектов: города, дороги, аэропорты и др.
Слайд 23 Интерактивные географические карты реализуются с использованием векторной графики
и связаны с базами данных, которые хранят всю необходимую информацию
об объектах, изображенных на картах.
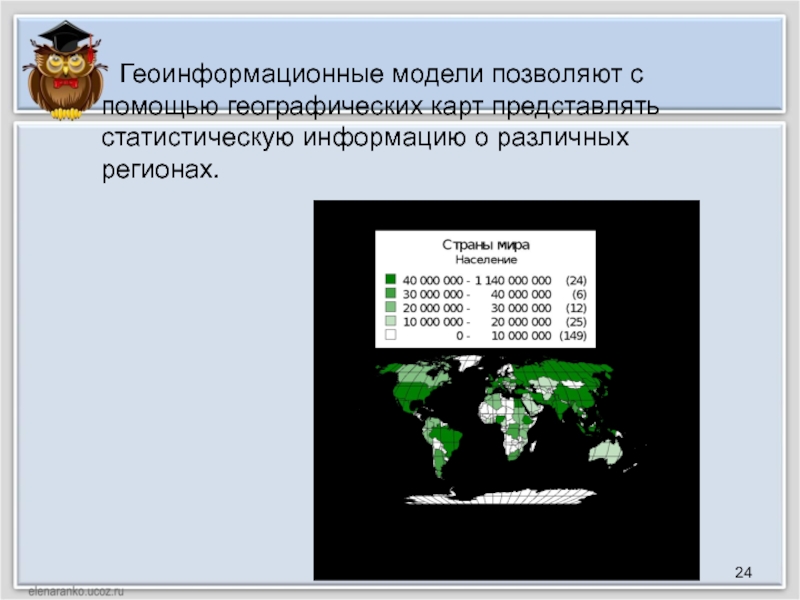
Слайд 24 Геоинформационные модели позволяют с помощью географических карт представлять
статистическую информацию о различных регионах.
Слайд 25Задание:
С помощью геоинформационной модели «Численность населения в странах мира» найдите
свой регион (страну) и выпишите следующую информацию:
Слайд 26Оптимизационное моделирование в экономике
Слайд 27 В сфере управления сложными системами применяется оптимизационное моделирование,
в процессе которого осуществляется поиск наиболее оптимального пути развития системы.
Оптимальное развитие соответствует экстремальному (максимальному или минимальному) значению выбранного целевого параметра.
Слайд 28Содержательная постановка проблемы
В ходе производственного процесса из
листов материала получают заготовки деталей двух типов А и Б
тремя различными способами, при этом количество получаемых заготовок при каждом методе различается.
Необходимо выбрать оптимальное сочетание способов раскроя, для того, чтобы получить 500 заготовок первого типа и 300 заготовок второго типа при расходовании наименьшего количества листов материала.
Слайд 29Компьютерная модель
Искать решение задачи путем создания и исследования
компьютерной модели в электронных таблицах Excel.
Исследование модели
Для поиска
оптимального выбора значений параметров, который соответствует минимальному значению целевой функции используем надстройку электронных таблиц Поиск решения.
Модель «Оптимизационное моделирование» хранится в файле model.xls
Слайд 30Вывод:
Таким образом, для изготовления 500 деталей А и 300 деталей
Б требуется
___ листов материала (целевая функция),
При этом необходимо раскроить листов
по
первому варианту______ (Х1)
по второму варианту_______(Х2)
по третьему варианту ______(Х3)
Слайд 31Домашнее задание
Садовый участок прямоугольной формы имеет площадь S=120. При каких
размерах длины и ширины участка длина изгороди будет наименьшей?
Составить геометрическую
и математическую модель. Провести расчеты.