История возникновения информатики как науки

кодировки символов для телетайпов. В честь Бодо названа единица скорости

передачи сигнала — БОД

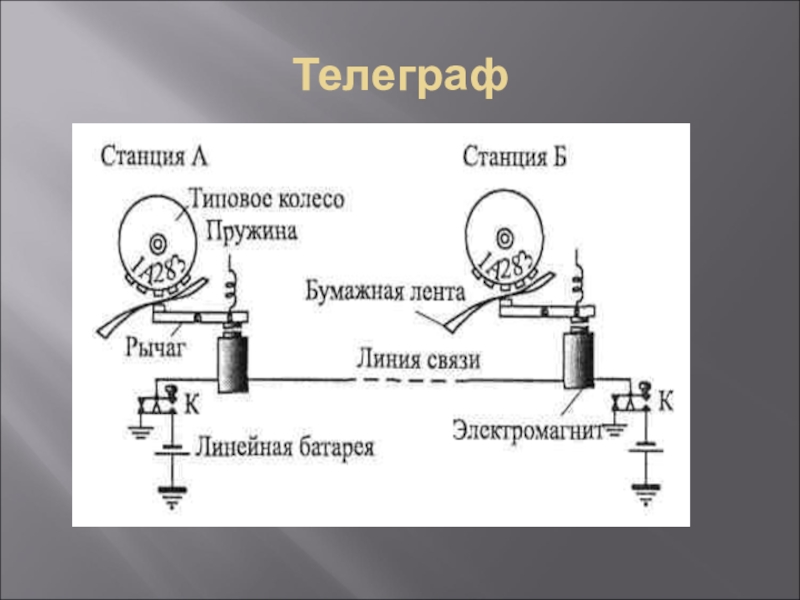
В 1872 году Бодо создал телеграфный аппарат многократного действия, при помощи которого можно было передавать по одной линии два и более сообщения.
Такой аппарат и все последующие устройства, которые были созданы по такому же принципу, получили название стартстопных.  До этого изобретения все телеграфные передачи велись с использованием азбуки Морзе  До этого изобретения все телеграфные передачи велись с использованием азбуки Морзе. Бодо впервые создал аппарат, который передавал сообщения, используя буквы латинского алфавита.

повсеместно. Он был назван Международный телеграфный код №1. Через два

года Бодо усовершенствовал свое изобретение и создал двукратный аппарат, который передавал информацию со скоростью 360 знаков в минуту. Еще через два года он создал уже пятикратный аппарат, скорость передачи в котором увеличилась по сравнению с первым в пять раз, а со вторым в 2,5 раза. Первые подобные аппараты были введены в эксплуатацию в 1877 году на линии Париж – Бордо. Благодаря аппарату Бодо появилась возможность использовать время интервалов между тире и точками. Это было достигнуто в результате работы на одной линии четырех или шести телеграфистов. Самыми популярными стали двукратные аппараты, которые передавали информацию на большие дистанции и использовались до конца ХХ века. Скорость передачи в таких аппаратах была 760 знаков за минуту. Помимо данного аппарата, Бодо разработал распределитель, дешифратор и печатающие механизм. Аппарат Бодо стал самым значимым достижением техники передачи информации на расстоянии в ХIХ веке.

наряду с исследованиями по физиологии нервной деятельности привело Винера к

привело Винера к формулировке идей и принципов кибернетики
Винер занимался также теоритичесой физикой, получил ряд значительных результатов в области математического анализа и теории вероятностей

и машине», 1948

точек зрения, философских взглядов, теоретических посылок, политических оценок и т.

п.

ШЕННОНОМ В РАБОТЕ «МАТЕМАТИЧЕСКАЯ ТЕОРИЯ СВЯЗИ» . ПОД ИНФОРМАЦИЕЙ ШЕННОН

ПОНИМАЛ ТОЛЬКО ТЕ ПЕРЕДАВАЕМЫЕ СООБЩЕНИЯ, КОТОРЫЕ УМЕНЬШАЮТ НЕОПРЕДЕЛЕННОСТЬ У ПОЛУЧАТЕЛЯ ИНФОРМАЦИИ. ТАКИМ ОБРАЗОМ, ИНФОРМАЦИЯ ИЗМЕРЯЕТСЯ РАЗНОСТЬЮ ЭНТРОПИЙ СИСТЕМЫ ДО И ПОСЛЕ ПОЛУЧЕНИЯ ИНФОРМАЦИИ, А САМА ИНФОРМАЦИЯ ВЫСТУПАЕТ КАК МЕРА ОТНОШЕНИЯ И ВЗАИМОСВЯЗИ МЕЖДУ СИСТЕМАМИ, ЯВЛЕНИЯМИ И ПРОЦЕССАМИ.

ПРОЕКТИРУЮТСЯ НА ОСНОВЕ ФУНДАМЕНТАЛЬНЫХ ПРИНЦИПОВ И ЗАКОНОВ ПЕРЕДАЧИ ИНФОРМАЦИИ, РАЗРАБОТАННЫХ

ШЕННОНОМ. В СООТВЕТСТВИИ С ТЕОРИЕЙ ИНФОРМАЦИИ ВНАЧАЛЕ ИЗ СООБЩЕНИЯ УСТРАНЯЕТСЯ ИЗБЫТОЧНОСТЬ, ЗАТЕМ ИНФОРМАЦИЯ КОДИРУЕТСЯ ПРИ ПОМОЩИ КОДОВ, УСТОЙЧИВЫХ К ПОМЕХАМ, И ЛИШЬ ПОТОМ СООБЩЕНИЕ ПЕРЕДАЕТСЯ ПО КАНАЛУ ПОТРЕБИТЕЛЮ. ЗНАЧИТЕЛЬНО БЫЛА СОКРАЩЕНА ИЗБЫТОЧНОСТЬ ТЕЛЕВИЗИОННЫХ, РЕЧЕВЫХ И ФАКСИМИЛЬНЫХ СООБЩЕНИЙ, ИМЕННО БЛАГОДАРЯ ТЕОРИИ ИНФОРМАЦИИ.

ШУМЫ В КАНАЛАХ СВЯЗИ С ТОЧКИ ЗРЕНИЯ СТАТИСТИКИ, РАССМАТРИВАЯ КАК

КОНЕЧНЫЕ МНОЖЕСТВА СООБЩЕНИЙ, ТАК И НЕПРЕРЫВНЫЕ МНОЖЕСТВА СООБЩЕНИЙ. РАЗВИТАЯ ШЕННОНОМ ТЕОРИЯ ИНФОРМАЦИИ ПОМОГЛА РЕШИТЬ ГЛАВНЫЕ ПРОБЛЕМЫ, СВЯЗАННЫЕ С ПЕРЕДАЧЕЙ СООБЩЕНИЙ, А ИМЕННО: УСТРАНИТЬ ИЗБЫТОЧНОСТЬ ПЕРЕДАВАЕМЫХ СООБЩЕНИЙ, ПРОИЗВЕСТИ КОДИРОВАНИЕ И ПЕРЕДАЧУ СООБЩЕНИЙ ПО КАНАЛАМ СВЯЗИ С ШУМАМИ. РЕШЕНИЕ ПРОБЛЕМЫ ИЗБЫТОЧНОСТИ ПОДЛЕЖАЩЕГО ПЕРЕДАЧЕ СООБЩЕНИЯ ПОЗВОЛЯЕТ МАКСИМАЛЬНО ЭФФЕКТИВНО ИСПОЛЬЗОВАТЬ КАНАЛ СВЯЗИ.

СИСТЕМАХ ТЕЛЕВИЗИОННОГО ВЕЩАНИЯ НА СЕГОДНЯШНИЙ ДЕНЬ ПОЗВОЛЯЮТ ПЕРЕДАВАТЬ ДО ШЕСТИ

ЦИФРОВЫХ ПРОГРАММ КОММЕРЧЕСКОГО ТЕЛЕВИДЕНИЯ, В ПОЛОСЕ ЧАСТОТ, КОТОРУЮ ЗАНИМАЕТ ОБЫЧНЫЙ СИГНАЛ АНАЛОГОВОГО ТЕЛЕВИДЕНИЯ. РЕШЕНИЕ ПРОБЛЕМЫ ПЕРЕДАЧИ СООБЩЕНИЯ ПО КАНАЛАМ СВЯЗИ С ШУМАМИ ПРИ ЗАДАННОМ СООТНОШЕНИИ МОЩНОСТИ ПОЛЕЗНОГО СИГНАЛА К МОЩНОСТИ СИГНАЛА ПОМЕХИ В МЕСТЕ ПРИЕМА, ПОЗВОЛЯЕТ ПЕРЕДАВАТЬ ПО КАНАЛУ СВЯЗИ СООБЩЕНИЯ СО СКОЛЬ УГОДНО МАЛОЙ ВЕРОЯТНОСТЬЮ ОШИБОЧНОЙ ПЕРЕДАЧИ СООБЩЕНИЯ. ТАКЖЕ, ЭТО ОТНОШЕНИЕ ОПРЕДЕЛЯЕТ ПРОПУСКНУЮ СПОСОБНОСТЬ КАНАЛА. ЭТО ОБЕСПЕЧИВАЕТСЯ ПРИМЕНЕНИЕМ КОДОВ, УСТОЙЧИВЫХ К ПОМЕХАМ, ПРИ ЭТОМ СКОРОСТЬ ПЕРЕДАЧИ СООБЩЕНИЙ ПО ДАННОМУ КАНАЛУ ДОЛЖНА БЫТЬ НИЖЕ ЕГО ПРОПУСКНОЙ СПОСОБНОСТИ

ИНФОРМАЦИИ ПО ТЕЛЕГРАФНОМУ ИЛИ ТЕЛЕФОННОМУ КАНАЛУ, НАХОДЯЩЕМУСЯ ПОД ВОЗДЕЙСТВИЕМ ЭЛЕКТРИЧЕСКИХ

ВОЗМУЩЕНИЙ ИЛИ ШУМА. ОН ПРИШЕЛ К ВЫВОДУ, ЧТО НАИЛУЧШЕЕ РЕШЕНИЕ ЗАКЛЮЧАЕТСЯ НЕ В ТЕХНИЧЕСКОМ УСОВЕРШЕНСТВОВАНИИ ЛИНИЙ СВЯЗИ, А В БОЛЕЕ ЭФФЕКТИВНОЙ УПАКОВКЕ ИНФОРМАЦИИ.

О СОДЕРЖАНИИ ЭТОГО ПОНЯТИЯ, ШЕННОН ПОКАЗАЛ, ЧТО ЭТО ИЗМЕРИМАЯ ВЕЛИЧИНА:

КОЛИЧЕСТВО ИНФОРМАЦИИ, СОДЕРЖАЩЕЙСЯ В ДАННОМ СООБЩЕНИИ, ЕСТЬ ФУНКЦИЯ ВЕРОЯТНОСТИ, ЧТО ИЗ ВСЕХ ВОЗМОЖНЫХ СООБЩЕНИЙ БУДЕТ ВЫБРАНО ДАННОЕ. ОН НАЗВАЛ ОБЩИЙ ПОТЕНЦИАЛ ИНФОРМАЦИИ В СИСТЕМЕ СООБЩЕНИЙ КАК ЕЕ “ЭНТРОПИЮ”. В ТЕРМОДИНАМИКЕ ЭТО ПОНЯТИЕ ОЗНАЧАЕТ СТЕПЕНЬ СЛУЧАЙНОСТИ (ИЛИ, ЕСЛИ УГОДНО, “ПЕРЕМЕШАННОСТИ”) СИСТЕМЫ. (ОДНАЖДЫ ШЕННОН СКАЗАЛ, ЧТО ПОНЯТИЕМ ЭНТРОПИИ ЕМУ ПОСОВЕТОВАЛ ВОСПОЛЬЗОВАТЬСЯ МАТЕМАТИК ДЖОН ФОН НЕЙМАН, УКАЗАВШИЙ, ЧТО, Т. К. НИКТО НЕ ЗНАЕТ, ЧТО ЭТО ТАКОЕ, У ШЕННОНА ВСЕГДА БУДЕТ ПРЕИМУЩЕСТВО В СПОРАХ, КАСАЮЩИХСЯ ЕГО ТЕОРИИ.)

количества информации, названную потом битом, как сообщение, представляющее один из

двух вариантов: например, “орел” — “решка”, или “да” — “нет”. Бит можно представить как или 0, или как присутствие или отсутствие тока в цепи.

На этом математическом фундаменте Шеннон затем показал, что любой канал связи имеет свою максимальную пропускную способность для надежной передачи информации. В действительности он доказал, что, хотя можно приблизиться к этому максимуму за счет искусного кодирования, достичь его невозможно.

как предел Шеннона, Каким образом можно приблизиться к пределу Шеннона?

Первый шаг заключается в том, чтобы воспользоваться избыточностью кода. Подобно тому как влюбленный мог бы лаконично написать в своей любовной записке “я лбл в”, путем эффективного кодирования можно сжать информацию, представив ее в наиболее компактной форме. С помощью специальных методов кодирования, позволяющих проводить коррекцию ошибок, можно гарантировать, что сообщение не будет искажено шумом.