Слайд 1Логические основы компьютера
Слайд 2Каждая логическая связка рассматривается как операция над логическими высказываниями и
имеет свое название и обозначение.
Логические операции.
Выделяют следующие логические операции:
инверсия;инверсия;
конъюнкция;
дизъюнкция; импликация;
эквиваленция.
Слайд 3Операция инверсия (отрицание):
Отрицание - это логическая операция, которая каждому простому
высказыванию ставит в соответствие составное высказывание, заключающееся в том, что
исходное высказывание отрицается.
Обозначается: ол
В естественном языке: соответствует словам "неверно, что..." и частице "не"
Диаграмма Эйлера-Венна:
Принимаемые значения: лрл
Диаграмма Эйлера-Венна:
В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, т.е. множеству получившемуся в результате отрицания множества соответствует множество, дополняющее его до универсального множества.
Слайд 4Операция конъюнкция
(лат. conjunctio — соединение)
(логическое умножение):
Конъюнкция - это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.
Обозначается: ол
В естественном языке: соответствует союзу "и"
Принимаемые значения: лрл
Диаграмма Эйлера-Венна:
В алгебре множеств конъюнкции соответствует операция пересечения множеств, т.е. множеству получившемуся в результате умножения множеств А и В соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.
Слайд 5Примеры:
10 делится на 2 (A - и). 5 больше
3 (B - и). 10 делится на 2 и 5
больше 3 (A B - и).
10 не делится на 2 (A - л). 5 больше 3 (B - и). 10 не делится на 2 и 5 больше 3 (A B - л).
10 делится на 2 (A - и). 5 не больше 3 (B - л). 10 делится на 2 и 5 не больше 3 (A B - л).
10 не делится на 2 (A - л). 5 не больше 3 (B - л). 10 делится на 2 и 5 больше 3 (A B - л).
Слайд 6Операция дизъюнкция (лат. disjunctio — разделение) (логическое сложение):
Дизъюнкция - это
логическая операция, которая каждым двум простым высказываниям ставит в соответствие
составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.
Обозначается: ол
В естественном языке: соответствует союзу "или"
Принимаемые значения: лрл
Слайд 7Примеры:
10 делится на 2 (A - и). 5 больше
3 (B - и).
10 делится на 2 или
5 больше 3 (A B - и).
10 не делится на 2 (A - л). 5 больше 3 (B - и).
10 не делится на 2 или 5 больше 3 (A B - и).
10 делится на 2 (A - и). 5 не больше 3 (B - л).
10 делится на 2 или 5 не больше 3 (A B - и).
10 не делится на 2 (A - л). 5 не больше 3 (B - л).
10 не делится на 2 или 5 не больше 3 (A B - л).
Слайд 8Операция импликация (лат. лат. implico — тесно связаны) (логическое сложение):
Импликация
- это логическая операция, ставящая в соответствие каждым двум простым
высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.
Обозначается: ол
В естественном языке: соответствует обороту "если ..., то ..."
Принимаемые значения: лрл
Слайд 9Примеры:
Данный четырёхугольник — квадрат (A - и). Около данного
четырёхугольника можно описать окружность (B - и). Если данный четырёхугольник
квадрат, то около него можно описать окружность (A B - и).
Данный четырёхугольник — не квадрат (A - л). Около данного четырёхугольника можно описать окружность (B - и). Если данный четырёхугольник не квадрат, то около него можно описать окружность (A B - и).
Данный четырёхугольник — квадрат (A - и). Около данного четырёхугольника нельзя описать окружность (B - л). Если данный четырёхугольник квадрат, то около него можно описать окружность (A B - л).
Данный четырёхугольник — не квадрат (A - л). Около данного четырёхугольника нельзя описать окружность (B - л). Если данный четырёхугольник не квадрат, то около него нельзя описать окружность (A B - и).
Слайд 10Операция эквиваленция
(двойная импликация):
Эквиваленция – это логическая операция, ставящая в
соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда
и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.
Обозначается: ол
В естественном языке: соответствует оборотам речи
"тогда и только тогда"; "в том и только в том случае"
Принимаемые значения: лрл
Слайд 11Примеры:
24 делится на 6 (A - и). 24 делится
на 3 (B - и). 24 делится на 6 тогда
и только тогда, когда 24 делится на 3 (A B - и).
24 не делится на 6 (A - л). 24 делится на 3 (B - и). 24 не делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - л).
24 делится на 6 (A - и). 24 не делится на 3 (B - л). 24 делится на 6 тогда и только тогда, когда 24 делится на 3 (A B - л).
24 не делится на 6 (A - л). 24 не делится на 3 (B - л). 24 не делится на 6 тогда и только тогда, когда 24 не делится на 3 (A B - и).
Слайд 12Порядок выполнения логических операций задается круглыми скобками.
Но для уменьшения
числа скобок договорились считать, что сначала выполняется операция
отрицания (“не”),
затем конъюнкция (“и”),
после конъюнкции — дизъюнкция (“или”)
и в последнюю очередь —
импликацияимпликация и эквиваленция
Слайд 13Логические формулы.
С помощью логических переменных и
символов логических операций любое высказывание можно формализовать, то есть заменить
логической формулой.
Определение логической формулы:
1. Всякая логическая переменная и символы "истина" ("1") и "ложь" ("0") — формулы.
2. Если А и В — формулы, то , (А &В), (А v В), (А B), (А В) — формулы.
3. Никаких других формул в алгебре логики нет.
В п. 1 определены элементарные формулы; в п. 2 даны правила образования из любых данных формул новых формул.
Слайд 14Пример:
Рассмотрим высказывание "если я куплю яблоки или абрикосы, то
приготовлю фруктовый пирог".
Обозначим буквой A высказывание: "купить яблоки", буквой
B - высказывание: "купить абрикосы", буквой C - высказывание: "испечь пирог".
Тогда высказывание "если я куплю яблоки или абрикосы, то приготовлю фруктовый пирог" формализуется в виде формулы:
(A v B)
C
Формула выполнимая - если при определенных сочетаниях значений переменных она принимает значение "истина" ("1") или "ложь" ("0").
Как показывает анализ формулы (A v B) C, при определённых сочетаниях значений переменных A, B и C она принимает значение "истина", а при некоторых других сочетаниях — значение "ложь".
Слайд 15Тавтология - тождественно истинная формула, или формула принимающая значение "истина"
("1") при любых входящих в нее значениях переменных.
Логически истинные
высказывания - высказывания, которые формализуются тавтологиями.
В качестве другого примера рассмотрим формулу А &A, которой соответствует, например, высказывание “Катя самая высокая девочка в классе, и в классе есть девочки выше Кати”. Очевидно, что эта формула ложна, так как либо А, либо A обязательно ложно.
Противоречие - тождественно ложная формула, или формула принимающая значение "ложь" ("0") при любых входящих в нее значениях переменных.
Слайд 16Логически ложные высказывания - высказывания, которые формализуются противоречиями.
Равносильные формулы
- две формулы А и В принимающие одинаковые значения, при
одинаковых наборах значений входящих в них переменных.
Равносильность двух формул алгебры логики обозначается символом
Равносильное преобразование формулы - замена формулы другой, ей равносильной.
Слайд 17Таблицы истинности.
Таблицу, показывающую, какие значения принимает составное высказывание при
всех сочетаниях (наборах) значений входящих в него простых высказываний, называют
таблицей истинности
составного высказывания.
Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.
Слайд 18Алгоритм построения таблицы истинности:
1.Подсчитать количество переменных n
в логическом выражении.
2. Определить число строк в таблице, которое равно
m = 2n.
3. Подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице: количество переменных + количество операций = количество столбцов.
4. Ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов.
5. Заполнить столбцы входных переменных наборами значений.
6. Провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.
Слайд 19Пример:
для формулы
построить таблицу истинности.
Решение:
Количество логических переменных
3, следовательно, количество строк в таблице истинности должно быть 2*2*2=8.
Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3+5=8.
Слайд 21
Основные законы логики.
Пусть высказывание A равносильно высказыванию B, тогда
можно записать A B.
В алгебре
логики выполняются следующие основные законы, позволяющие производить тождественные преобразования логических выражений.
1. Законы коммутативности:
2. Законы ассоциативности:
Слайд 223. Законы дистрибутивности:
4. Законы де Моргана:
5. Законы поглощения:
6. Закон противоречия:
7.
Закон исключенного третьего:
8. Закон двойного отрицания:
9. Закон контрпозиции:
Слайд 23В алгебре логики доказано, что любую логическую функцию можно выразить
через комбинацию логических операций отрицание ("не"), конъюнкциюВ алгебре логики доказано,
что любую логическую функцию можно выразить через комбинацию логических операций отрицание ("не"), конъюнкцию ("и") и дизъюнкцию ("или").
Импликацию можно выразить через дизъюнкцию и отрицание:
Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:
Слайд 24Двоичное кодирование и алгебра логики.
Математический аппарат алгебры логики очень удобен
для описания того, как функционируют аппаратные средства компьютера, поскольку основной
системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: "истина" (“1”) и "ложь" (“0”).
Из этого следует два вывода:
одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
Данные и команды представляются в виде двоичных последовательностей различной структуры и длины.
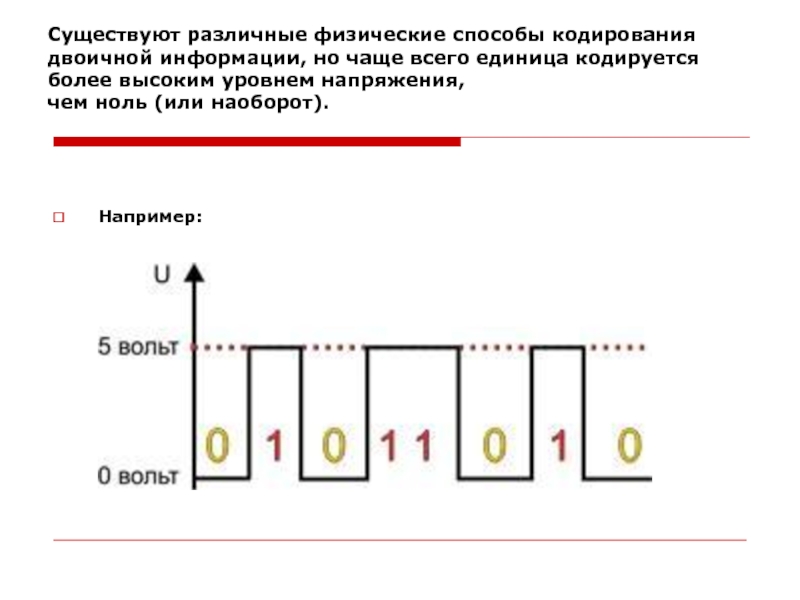
Слайд 25Существуют различные физические способы кодирования двоичной информации, но чаще всего
единица кодируется более высоким уровнем напряжения,
чем ноль (или наоборот).
Например:
Слайд 26Логический элемент компьютера — это часть электронной логичеcкой схемы, которая
реализует элементарную логическую функцию.
Логическими элементами компьютеров являются
электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и другие (называемые также вентилями), а также триггер.
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем. Работу логических элементов описывают с помощью таблиц истинности.
Слайд 27 Для хранения информации используются триггеры.
Триггер
— это электронная схема, широко применяемая в регистрах компьютера для
надёжного запоминания одного разряда двоичного кода. Триггер имеет два устойчивых состояния, одно из которых соответствует двоичной единице, а другое - двоичному нулю.
Термин триггер происходит от английского слова trigger - защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает “хлопанье”. Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить (“перебрасываться”) из одного электрического состояния в другое и наоборот.
Самый распространённый тип триггера собирается из четырех логических элементов "И-НЕ" (причем два из них играют вспомогательную роль) — так называемый RS-триггер (S и R, соответственно, от английских set — установка, и reset — сброс).
Условное обозначение триггера:
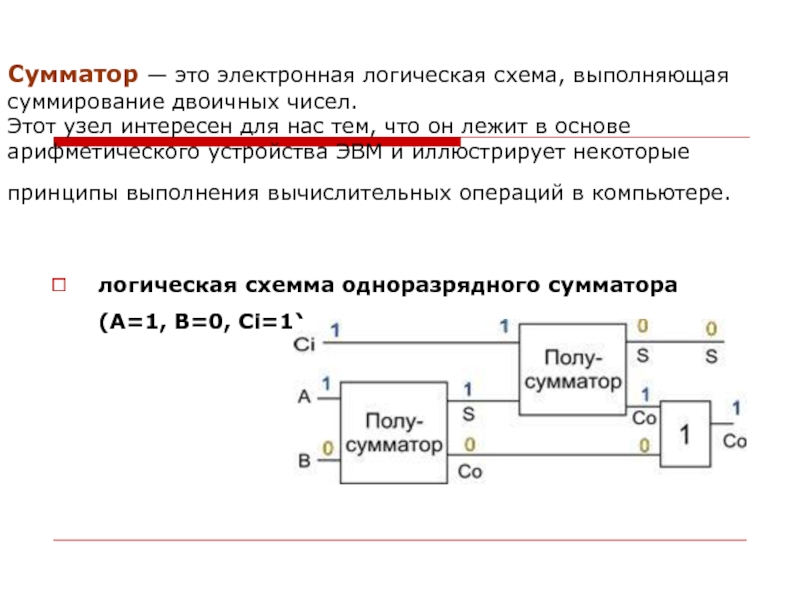
Слайд 28Сумматор — это электронная логическая схема, выполняющая суммирование двоичных чисел.
Этот узел интересен для нас тем, что он лежит в
основе арифметического устройства ЭВМ и иллюстрирует некоторые принципы выполнения вычислительных операций в компьютере.
логическая схемма одноразрядного сумматора
(А=1, В=0, Ci=1)