Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логические основы работы компьютера 9 класс
Содержание
- 1. Логические основы работы компьютера 9 класс
- 2. СодержаниеОпределение логикиОсновоположники логикиОсновные понятия логикиФормализация логических высказыванийЛогические
- 3. Определение логики Логика – наука о законах и
- 4. Основоположники логикиАристотель (4 в. до н.э.) –
- 5. Основные понятия логикиПонятие - форма мышления, которая
- 6. Формализация логических высказыванийВысказываниесоставныепростые Формализовать
- 7. Логические связки и обозначения
- 8. « Если погода солнечная, то можно косить
- 9. Инверсия (НЕ)Конъюнкция (И)Таблица истинности Ее построение позволяет определить
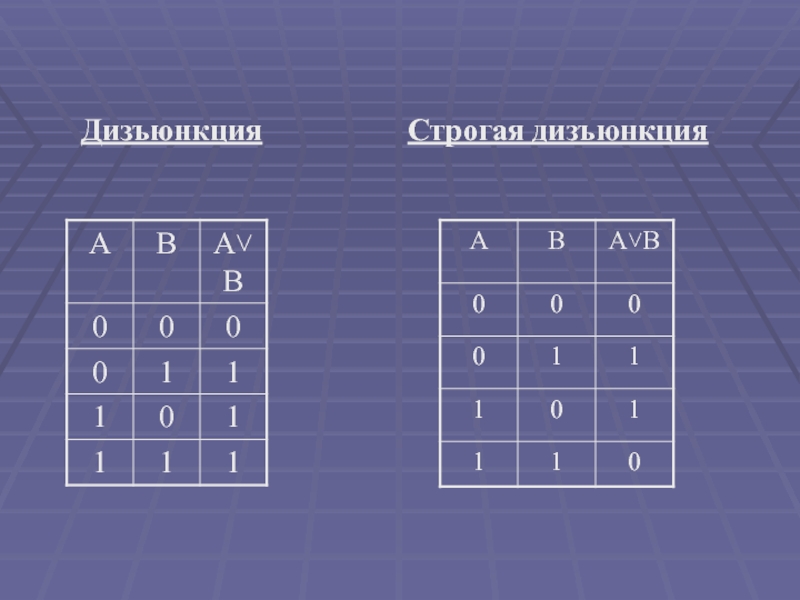
- 10. ДизъюнкцияСтрогая дизъюнкция
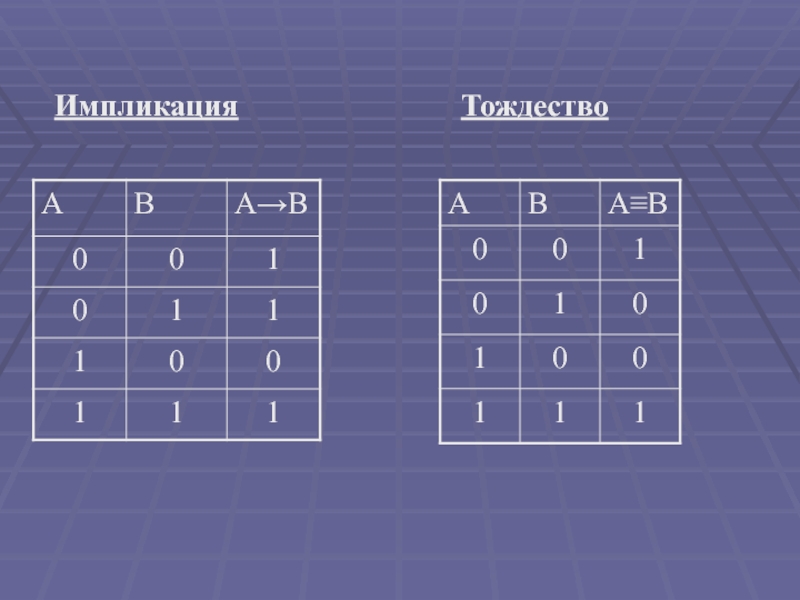
- 11. ИмпликацияТождество
- 12. Пример построения таблицы истинности по формуле: F=Ā^(B˅C)
- 13. Построение логической функции по таблице истинностиАлгоритм построения:Отметить
- 14. F=Ā^B + A^B Пример построения логической функции по таблице истинности
- 15. Законы логики1.Отсутствие степеней и коэффициентов: A^A=A; A˅A=A;
- 16. Упрощение логических выраженийХ=А ^ В ˅ В=А
- 17. Благодарю за внимание!
- 18. Скачать презентанцию
СодержаниеОпределение логикиОсновоположники логикиОсновные понятия логикиФормализация логических высказыванийЛогические связки и обозначенияТаблицы истинностиПример построения таблицы истинностиПостроение логической функции по таблице истинностиПример построения логической функцииЗаконы логикиУпрощение логических выражений
Слайды и текст этой презентации
Слайд 2Содержание
Определение логики
Основоположники логики
Основные понятия логики
Формализация логических высказываний
Логические связки и обозначения
Таблицы
истинности
Пример построения таблицы истинности
Построение логической функции по таблице истинности
Пример построения
логической функцииЗаконы логики
Упрощение логических выражений
Слайд 3Определение логики
Логика – наука о законах и формах человеческого мышления.
Формальная
логика связана с анализом обычных содержательных умозаключений, выраженных разговорным языком.
Математическая
логика изучает вопросы применения математических методов для решения логических задач, построения логических схем.Булева «алгебра» - система обозначений и правил, применяемых к различным объектам.
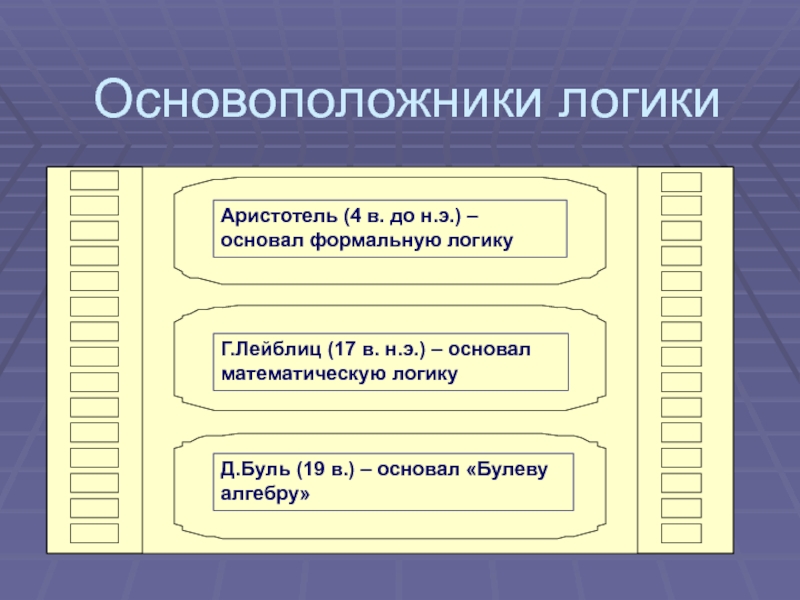
Слайд 4Основоположники логики
Аристотель (4 в. до н.э.) – основал формальную логику
Г.Лейблиц (17 в. н.э.) – основал математическую логику
Д.Буль (19 в.)
– основал «Булеву алгебру»Слайд 5Основные понятия логики
Понятие - форма мышления, которая выделяет существенные признаки
объекта, предмета.
Суждение – мысль, в которой что-либо утверждается, отрицается.
Умозаключение –
принцип мышления позволяющий на основе одного или нескольких суждений получить новое знание.Высказывание - повествовательное предложение, истинное или ложное.
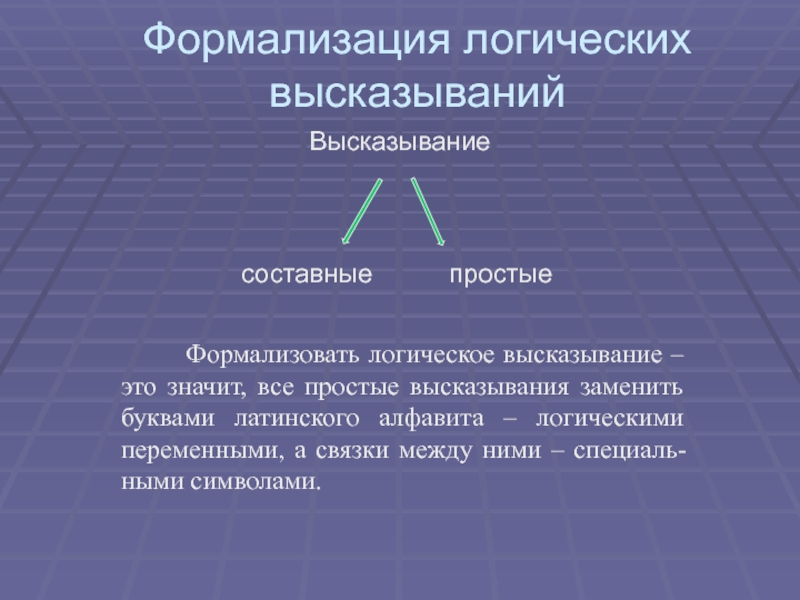
Слайд 6Формализация логических высказываний
Высказывание
составные
простые
Формализовать логическое высказывание –
это значит, все простые высказывания заменить буквами латинского алфавита –
логическими переменными, а связки между ними – специаль-ными символами.Слайд 8« Если погода солнечная, то можно косить сено, если погода
пасмурная, то лучше идти за грибами»
А- погода солнечная
В- косить сено
С-
идти за грибамиF=(А→В) ^ (Ā→С)
Задача:
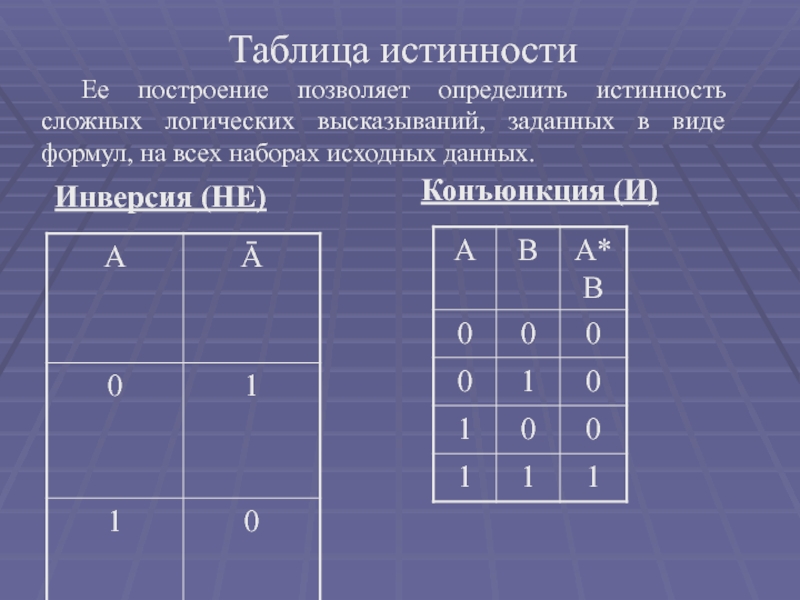
Слайд 9Инверсия (НЕ)
Конъюнкция (И)
Таблица истинности
Ее построение позволяет определить истинность сложных логических
высказываний, заданных в виде формул, на всех наборах исходных данных.
Слайд 13Построение логической функции по таблице истинности
Алгоритм построения:
Отметить в таблице истинности
строки, в которых результирующее выражение истинно (=1)
2) Для выбранных строк
соединить операцией логического умножения содержимое левых столбцов таблицы; при этом если в таблице стоит ноль, пишем исходное высказывание с отрицанием, в противном случае – без отрицания3) Соединить полученные выражения операцией логического сложения
Слайд 15Законы логики
1.Отсутствие степеней и коэффициентов: A^A=A; A˅A=A; A^1=1; А^1=A
2.Закон двойного отрицания: ¬ Ā= А
3.Закон исключения третьего: А˅Ā=1
4.Закон противоречия: A^Ā=0
5.Коммутативный закон: А˅B=B˅A; A^B=B^A
6.Ассоциативный закон: (A˅B)˅C=A˅(B˅C); (A^B)^C=A^(B^C)
7.Дистрибутивный: (A˅B) ^C=(A^C)˅(B^C); (A^B) ˅ C=(A ˅ C)^(B ˅ C)
8.Законы де Моргана: ¬ (A^B)= ¬ A ˅ ¬ B: ¬ (A ˅ B)= ¬ A^ ¬ B
9.Формулы склеивания (А ^ В) ˅(А ^ В)=А; (А ˅ В) ^(А ˅ В)=А
10. Формулы поглощения А ˅(А ^ В)=А; А ^(А ˅ В)=А; А ˅(Ā ^ В)=А ˅ В
А ^(Ā ˅ В)=А ^ В
11. Замена операций А ≡ В=(А ^ В) ˅(Ā ^ В); А ≡ В=(Ā ˅ В) ^(А ˅ В);
А ≡ В=(А→В) ^(А→В); А → В= Ā ˅ В
Слайд 16Упрощение логических выражений
Х=А ^ В ˅ В=А ˅ В ˅
В=А ˅ В
У=В ^ С ˅ С=(В ˅
С) ^ С= С
Z=A ^ C ˅ B ^ C=A ˅ C ˅ B ^ C=A ˅ C