Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Математическая основа покадровой анимации
Содержание
- 1. Математическая основа покадровой анимации
- 2. С помощью компьютера в настоящее время решаются
- 3. История развития компьютерной графики началась уже в
- 4. Процесс воспроизведения и обработки изображенияпредставление геометрических изображенийподготовка изображений к воспроизведениювзаимодействие конструктора с изображением
- 5. На плоскости точку представляют с помощью дву
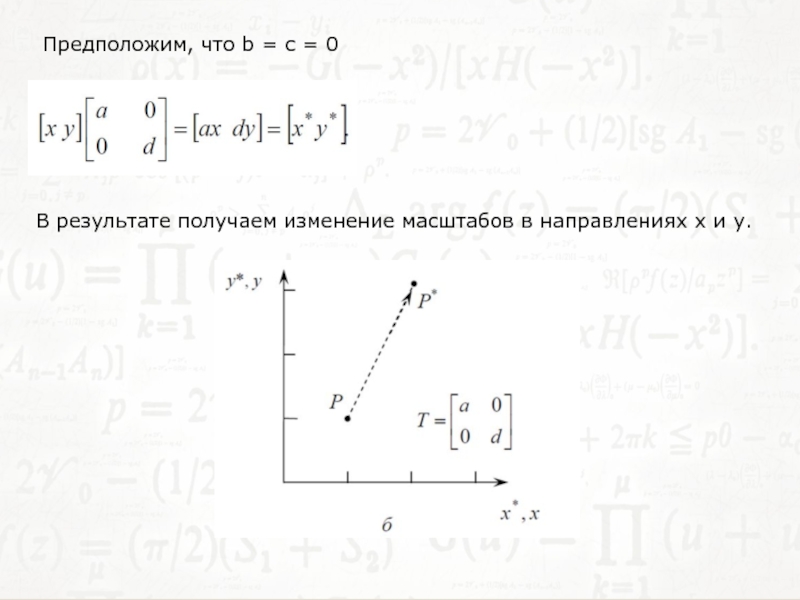
- 6. Предположим, что b = c =
- 7. Предположим, что b = c = 0,
- 8. Если b = c = 0, а
- 9. Нам необходимо создать движущуюся анимированную фигуру, которая будет уменьшаться в точку H(-3;-2). Обозначим каждую фигуру цифрой.Исследование132465
- 10. Выполним пять кадров движения. В каждом кадре
- 11. Перемещение 1 квадрата – «Тело»G(6;5)H(-3;-2)a=GH=(-9;-7)b=GO=(-6;-8)При перемещение сложной
- 12. ВычисленияКадр 1b1=(6;8)+1/5(-9;-7)=(4,2;3,6)Кадр 2b2=(6;8)+2/5(-9;-7)=(2,4;2,2)
- 13. Кадр 3b3=(6;8)+3/5(-9;-7)=(0,6;0,8)Кадр 4b4=(6;8)+4/5(-9;-7)=(-1,2;-0,6)
- 14. По аналогии с квадратом 1 производится расчет
- 15. После я предположила, что все квадраты должны
- 16. Вычисления
- 17. Слайд 17
- 18. .
- 19. Перемещение круга рассчитывается так же, как и
- 20. Кадр 1b1=(6;8)+1/5(-9;-10)=(4,2;6) – координаты центра окружностиr=0.8 Кадр 2b2=(6;8)+2/5(-9;-10)=(2,4;4)r=0.6 Кадр 3b3=(6;8)+3/5(-9;-10)=(0,6;2)r=0.4 Кадр 4b4=(6;8)+4/5(-9;-10)=(-1,2;0)r=0.2Кадр 5b5=(6;8)+5/5(-9;-10)=(-3;-2)r=0Вычисления
- 21. В ходе проведённого информатико-математического исследования на примере
- 22. Спасибо за внимание!
- 23. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Математическая основа покадровой анимации
Выполнила: Янмурзаева М. А.
МБОУ СОШ № 120;
11 А класс
Слайд 2С помощью компьютера в настоящее время решаются многие задачи геометрического
характера, к таким задачам можно отнести основы покадровой анимации.
Задачи исследования:
Доказать, что математика является основой покадровой анимации.
Изучить элементы векторной алгебры и аналитической геометрии, применить на практике числовые методы решения математических задач
Выполнить расчеты для покадрового изменения простейших геометрических фигур.
Слайд 3История развития компьютерной графики началась уже в 20 веке и
продолжается сегодня. Не секрет то, что именно графика способствовала быстрому
росту быстродействию компьютеров. В 1940-1970гг (эра до персональных компьютеров) были заложены математические основы.Слайд 4Процесс воспроизведения и обработки изображения
представление геометрических изображений
подготовка изображений к воспроизведению
взаимодействие
конструктора с изображением
Слайд 5На плоскости точку представляют с помощью дву ее координат.
Последовательность
точек геометрического объекта, каждая из которых характеризуется значением координат вектора
относительно выбранной системы координат, может быть представлена как матрица чисел. Положением этих точек управляют путем преобразования матрицы.Слайд 9Нам необходимо создать движущуюся анимированную фигуру, которая будет уменьшаться в
точку H(-3;-2). Обозначим каждую фигуру цифрой.
Исследование
1
3
2
4
6
5
Слайд 10Выполним пять кадров движения. В каждом кадре происходят следующие операции:
Найти
G – центр фигуры. Тогда в каждом кадре сначала происходит
смещение Tb плоскости на вектор.b=GO(О- начало координат). При этом центр квадрата совмещается с началом координат.
Затем происходит равномерное масштабирование плоскости с коэффициентом, зависящим от номера кадра: в первом кадре это 0.8, во втором 0.6 и т.д.
Масштабированный квадрат возвращается в точку, промежуточную между G и H.
Вектор bk соответствующей трансляции так же зависит от номера кадра (k):
bk=-b+(k/10)a;
где а – это вектор, соединяющий центр фигуры с точкой H.
Алгоритм действий
Слайд 11Перемещение 1 квадрата – «Тело»
G(6;5)
H(-3;-2)
a=GH=(-9;-7)
b=GO=(-6;-8)
При перемещение сложной фигуры я предположила,
что при вычислениях у всех квадратов отрезок а=GH должен быть
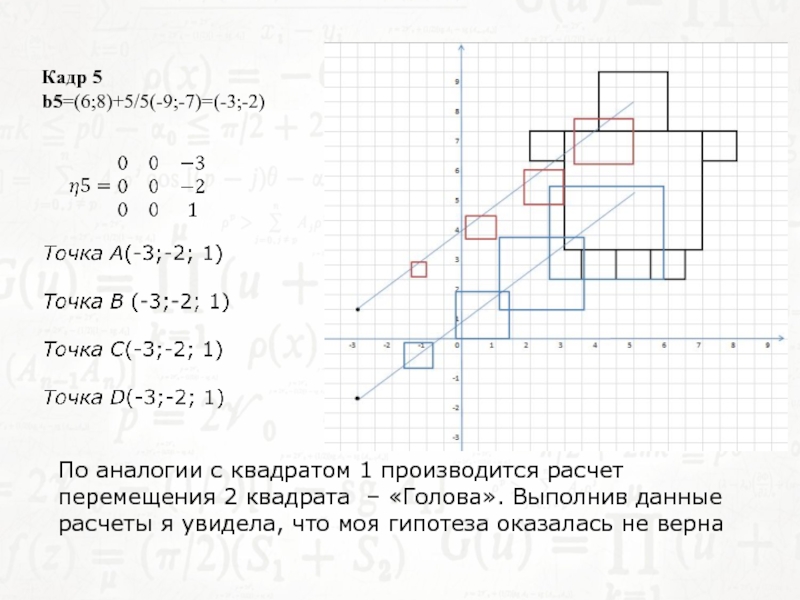
одинаковым.Слайд 14По аналогии с квадратом 1 производится расчет перемещения 2 квадрата
– «Голова». Выполнив данные расчеты я увидела, что моя гипотеза
оказалась не вернаКадр 5
b5=(6;8)+5/5(-9;-7)=(-3;-2)
Слайд 15После я предположила, что все квадраты должны перемещаться в одну
точку H(-3;-2), т.е. для них не существует универсального показателя a=GH.
Следовательно, при расчете каждого квадрата значение отрезка a=GH будет различным.Перемещение 1 квадрата мы оставляем таким же, а вот 2 изменяем.
H(-3;-2)
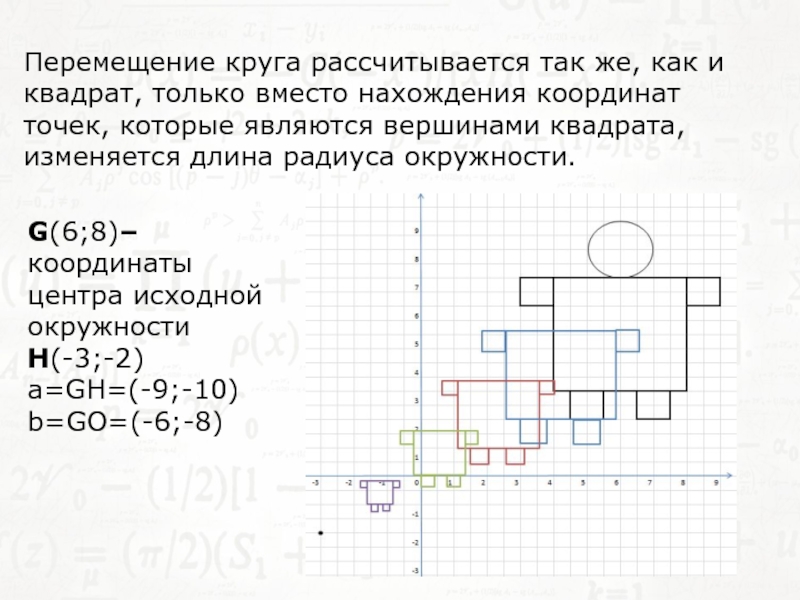
Слайд 19Перемещение круга рассчитывается так же, как и квадрат, только вместо
нахождения координат точек, которые являются вершинами квадрата, изменяется длина радиуса
окружности.G(6;8)– координаты центра исходной окружности
H(-3;-2)
a=GH=(-9;-10)
b=GO=(-6;-8)