Разделы презентаций

Многовариантное решение заданий ЕГЭ

Содержание

Содержание (начало)Задание 01-В01. Найти значение выражения: Задание 01-В02. Решите уравнение: Задание 01-В03. Решите уравнение: Задание 01-В04. Найти значение выражения:

Слайды и текст этой презентации

Слайд 1Многовариантное
решение заданий ЕГЭ


(задания взяты из пособия для самостоятельной подготовки
«Математика. ЕГЭ-2006.

Учебно-тренировочные тесты»
под редакцией Ф. Ф. Лысенко, изд. «Легион», 2006
(сокращение: 00-000,
где

00 и 000 соответственно номер варианта и задания)

Ю. Хапий,
учитель информатики
Город Самара, МБОУ СОШ № 10 «Успех»
2012 год городского округа Самара

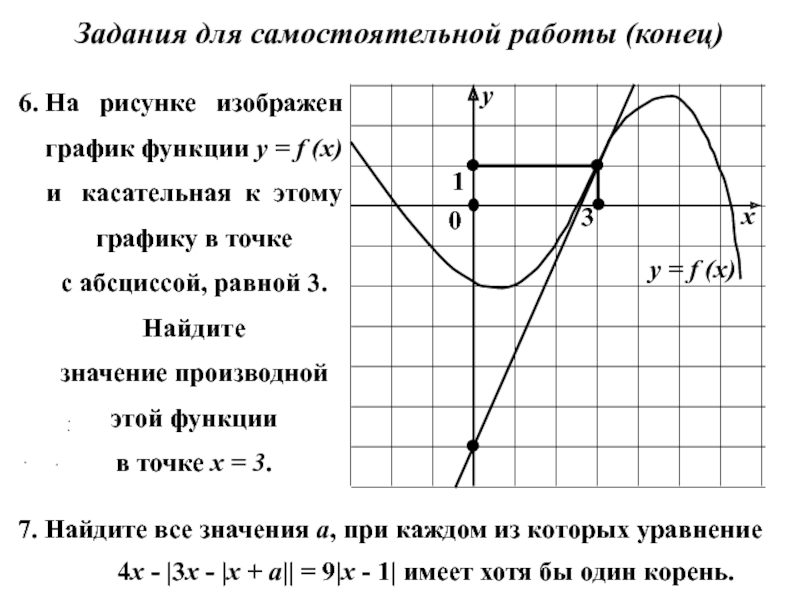
Многовариантноерешение заданий ЕГЭ(задания взяты из пособия для самостоятельной подготовки«Математика. ЕГЭ-2006. Учебно-тренировочные тесты»под редакцией Ф. Ф. Лысенко, изд.

Слайд 2Содержание (начало)
Задание 01-В01. Найти значение выражения:
Задание 01-В02. Решите уравнение:


Задание 01-В03. Решите уравнение:
Задание 01-В04. Найти значение выражения:

Содержание (начало)Задание 01-В01. Найти значение выражения: Задание 01-В02. Решите уравнение: Задание 01-В03. Решите уравнение: Задание 01-В04. Найти

Слайд 3Задание 01-В05. Функция y = f (x) определена

на отрезке [-6; 6]. На рисунке изображен ее график. Укажите

число промежутков, на которых отрицательна функция y = f '(x).

Содержание (конец)

Задание 01-В06. Найдите наибольшее значение функции

Задания для самостоятельной работы из ЕГЭ 2010 года.

Задание 01-В05. Функция y = f (x) определена на отрезке [-6; 6]. На рисунке изображен

Слайд 4Задание 01-В01.
Найти значение выражения:

Решение.
Вариант № 1.
Так как


Задание 01-В01.Найти значение выражения: Решение.Вариант № 1.Так как

Слайд 6следовательно,
Так как

то
Ответ:

следовательно, Так кактоОтвет:

Слайд 7Вариант № 2.
Так как
от переменны мест сомножителей произведение не меняется,

то

Вариант № 2.Так какот переменны мест сомножителей произведение не меняется,то

Слайд 8Так как
то

Так както

Слайд 9
Так как

Так как

Слайд 11Задание 01-В02.
Решите уравнение:
Решение.
Вариант № 1.
Так как
то

Задание 01-В02.Решите уравнение: Решение.Вариант № 1.Так както

Слайд 12Так как
то

Так както

Слайд 13 (нулевая степень любого положительного основания

равна единице), следовательно,


Так как
логарифм единицы по любому основанию равен нулю

(по определению логарифма

то

(нулевая степень любого положительного основания равна единице), следовательно, Так каклогарифм единицы по любому основанию равен

Слайд 14Так как
то

Ответ:

.

Так както

Слайд 15Вариант № 2.
Замечание. При варианте № 2 решения
использовалась операция

«потенцирование»
Произведенные преобразования
в двух вариантах решения равносильны,
что не требует проверки

полученного результата.
Вариант № 2.Замечание. При варианте № 2 решения использовалась операция «потенцирование» Произведенные преобразованияв двух вариантах решения равносильны,что

Слайд 16Задание 01-В03.
Решите уравнение:
Решение.
Вариант № 1.
Так как

Задание 01-В03.Решите уравнение: Решение.Вариант № 1.Так как

Слайд 19

Ответ:

.

∅

Слайд 20Задание 01-В04.
Найти значение выражения:
Решение.
Вариант № 1.
Так как
то

Задание 01-В04.Найти значение выражения: Решение.Вариант № 1.Так както

Слайд 21

Ответ:
.

Ответ:.

Слайд 22Вариант № 2.
Пусть
тогда
Решим систему:

Вариант № 2. Пусть тогда Решим систему:

Слайд 23
(При решении использовалась теорема Виета:
Так как от перемены мест

слагаемых сумма не меняется,
то согласно введенным обозначениям получим:
Аналогично находим:

(При решении использовалась теорема Виета: Так как от перемены мест слагаемых сумма не меняется,то согласно введенным обозначениям

Слайд 24Следовательно,



Следовательно,

Слайд 25Функция

определена на отрезке [-6; 6].
На рисунке изображен ее график.
Укажите

число промежутков,
на которых отрицательна функция .

Задание 01-В05.


Функция определена на отрезке [-6; 6].На рисунке

Слайд 26Решение.
Вариант № 1.

Из графика заданной функции, показанном на рисунке, следует

ее непрерывность на отрезке [-6; 6].

Согласно условию задачи в любой

точке отрезка [-6; 6] существует производная функции .

Если дифференцируемая функция ,
убывает на интервале ,
то для любого х0 из интервала .

Определим по графику заданной функции, показанном на рисунке, количество промежутков, где функция убывает:
]-4; -3[, ]-2; 1[, ]3; 4[, ]5; 6[, таких промежутков – четыре.

Ответ: количество промежутков,
в которых , равно четырем.



Решение.Вариант № 1.Из графика заданной функции, показанном на рисунке, следует ее непрерывность на отрезке [-6; 6].Согласно условию

Слайд 27Вариант № 2.

Так как убывающая и дифференцируемая на интервале



функция f

удовлетворяет условию



то количество промежутков, где функция



убывает - четыре

(]-4; -3[,

]-2; 1[, ]3; 4[, ]5; 6[).




Вариант № 2.Так как убывающая и дифференцируемая на интервалефункция f удовлетворяет условию то количество промежутков, где функцияубывает

Слайд 28 Найдите наибольшее

Задание 01-В06.
значение функции
Вариант № 1.
Так как для существования заданной функции
необходимо существование квадратного корня,
входящего в ее выражение,
то значения х ограничены условием: .

Следовательно, наибольшее значение заданной функции будем определять для .

Найдем значения х, при которых :


Найдите наибольшее

Слайд 29Найдем значение заданной функции при

.
для: х = 0,25 у = - 0,25; х = 1,25 у = 0,75.
Определим поведение функции на промежутке .

Пусть х = 2, тогда следовательно,

заданная функция на промежутке убывает.

Из полученных значений выбираем наибольшее: у = 0,75.




(Возможен другой подход для определения поведения функции на промежутке .


Найдем значение заданной функции при

Слайд 30использованы понятия бесконечно

малой и большой функции:

k – любое число).

Так как в точке х = 1,25 функция имеет максимум, поскольку



то, начиная с указанной точки,
функция убывает с учетом значения найденного предела.)

Ответ: наибольшее значение функции равно 0,75 при х = 1,25.


использованы понятия бесконечномалой и большой функции:

Слайд 31Вариант № 2.

Выполним равносильные преобразования для

:





Так

как то максимальное значение

у достигается при следовательно, х = 1,25.

Находим значение .




Вариант № 2.Выполним равносильные преобразования для

Слайд 32
Вариант № 3.

Пусть

,

тогда ,


следовательно, . Или .


Так как то максимальное значение у

достигается , при где t = 2.


Находим значение .


(Рассуждения проведены для .)








Вариант № 3.Пусть

Слайд 33Вариант № 4.

Выполним равносильные преобразования для

:



Найдем значения х

при условии максимального значения у.

Итак, .

Из полученного выражения для х следует, что

Вариант № 4.Выполним равносильные преобразования для

Слайд 34Значение для х определим
при условии максимального значения для

:


Замечание.

Последние три варианта решения связаны
с

преобразованием заданной функции к выражению,
математический анализ которого
позволяет сразу ответить на вопрос задания.

Первый вариант приводит к решению при использовании
правила нахождения наибольшего значения функции
и не требует «математической смекалки».
Значение для х определимпри условии максимального значения для : Замечание.Последние три

Слайд 352. Найти значение выражения

.

.

Задания для самостоятельной работы (начало)

1. Найти корень уравнения .

.

3. Решите систему уравнений

4. Решите неравенство

.

5. Найдите на отрезке наибольшее значение функции

.

2. Найти значение выражения

Слайд 36.
Задания для самостоятельной работы (конец)
.
.
.
7. Найдите все значения а,

при каждом из которых уравнение

4х - |3x - |x + a|| = 9|x - 1| имеет хотя бы один корень.

6. На рисунке изображен
график функции y = f (x)
и касательная к этому
графику в точке
с абсциссой, равной 3.
Найдите
значение производной
этой функции
в точке х = 3.







x

y

1

3

0

y = f (x)

. Задания для самостоятельной работы (конец)...7. Найдите все значения а, при каждом из которых уравнение

Похожие презентации

Из чего состоит? Что умеет? 3 класс Из чего состоит? Что умеет? 3 класс 348
"Компьютерная графика" 272
Простейшая анимация средствами MS PowerPoint Простейшая анимация средствами MS PowerPoint 376
Виды носителей информации Виды носителей информации 505
История ЭВМ История ЭВМ 362
Презентация по теме Презентация по теме "Файл и файловые системы" 8 класс 310
ghh ghh 504
Персональный компьютер как система (7 класс) Персональный компьютер как система (7 класс) 637
Принтеры Принтеры 359
Действия с фрагментом текста Действия с фрагментом текста 483
М?тін ?зінділерімен ж?мыс М?тін ?зінділерімен ж?мыс 309
Взаимодействующие параллельные процессы Взаимодействующие параллельные процессы 411
Информация. Информационные процессы Информация. Информационные процессы 431
Адресация компьютеров в сети Адресация компьютеров в сети 625
ОБЪЕКТЫ ОКРУЖАЮЩЕГО МИРА ОБЪЕКТЫ ОКРУЖАЮЩЕГО МИРА 466
Программные средства и технологии обработки текстовой информации Программные средства и технологии обработки текстовой информации 360
Профессия программист Профессия программист 433
Различные способы вычисления площадей фигур.Метод Монте - Карло. Различные способы вычисления площадей фигур.Метод Монте - Карло. 325
Компьютерные коммуникации. Виды компьютерных сетей Компьютерные коммуникации. Виды компьютерных сетей 502
Презентация по информатике Презентация по информатике "Устройство, принцип работы и правило эксплуатации фотоаппаратов." 325

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно  хранить и делиться своими презентациями с другими пользователями.

Для правообладателей

Яндекс.Метрика