Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Моделирование и формализация. Разработка и исследование математических моделей на компьютере
Содержание
- 1. Моделирование и формализация. Разработка и исследование математических моделей на компьютере
- 2. Моделирование – это метод познания, состоящий в
- 3. Модели – упрощенное подобие реального объектаИнформационные моделиНатуральные моделиФормализация – замена натурального объекта его моделью
- 4. Натуральные или материальные модели
- 5. Информационные моделиТабличная информационная модельИерархическая информационная модельСетевая информационная модель
- 6. В табличной информационной модели перечень однотипных объектов
- 7. В иерархической информационной модели объекты распределены по
- 8. Сетевые информационные модели применяются для отражения систем
- 9. Модели, описывающие состояние системы в определенный момент
- 10. С помощью формальных языков строятся формальныеинформационные модели
- 11. Логическая схема полусумматораИИЛИНЕИАВР=А&В
- 12. Математическая модель – это система математических соотношений
- 13. Основные этапы разработки и исследования моделей на
- 14. Математические модели:Приближенное решение уравненийОпределение экстремума функцииВычисление площади криволинейной трапеции
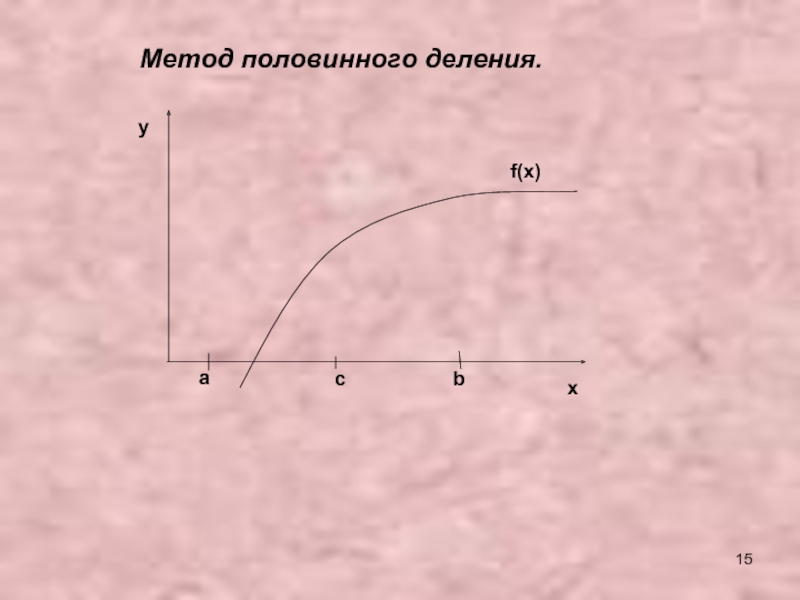
- 15. abcf(x)yxМетод половинного деления.
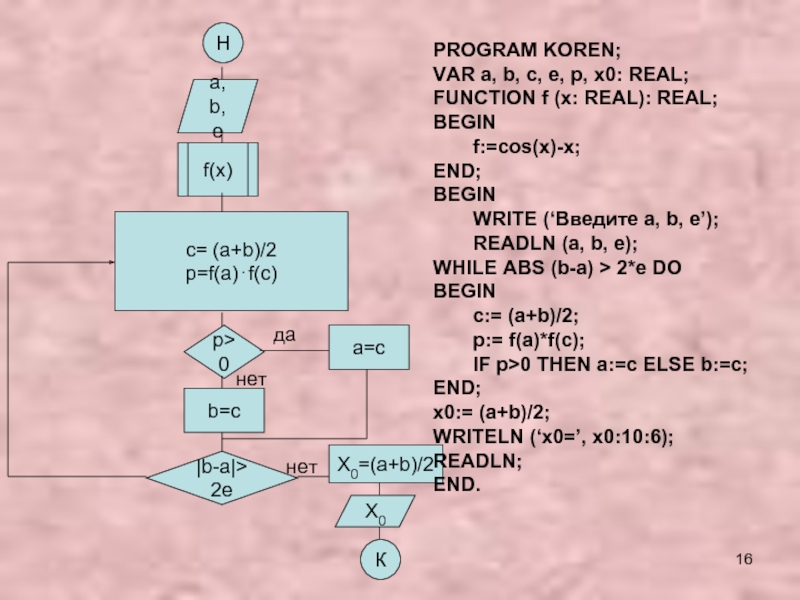
- 16. Нa, b, ef(x)c= (a+b)/2p=f(a)⋅f(c)p>0b=c|b-a|>2eX0=(a+b)/2X0Кa=cданетнетPROGRAM KOREN;VAR a, b,
- 17. Cos(x) – x = 0
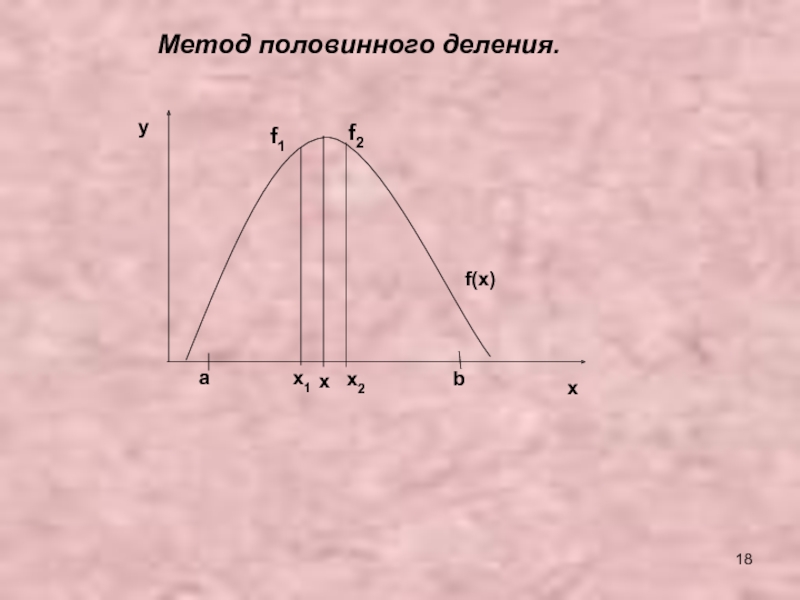
- 18. abf(x)yxxx2x1f1f2Метод половинного деления.
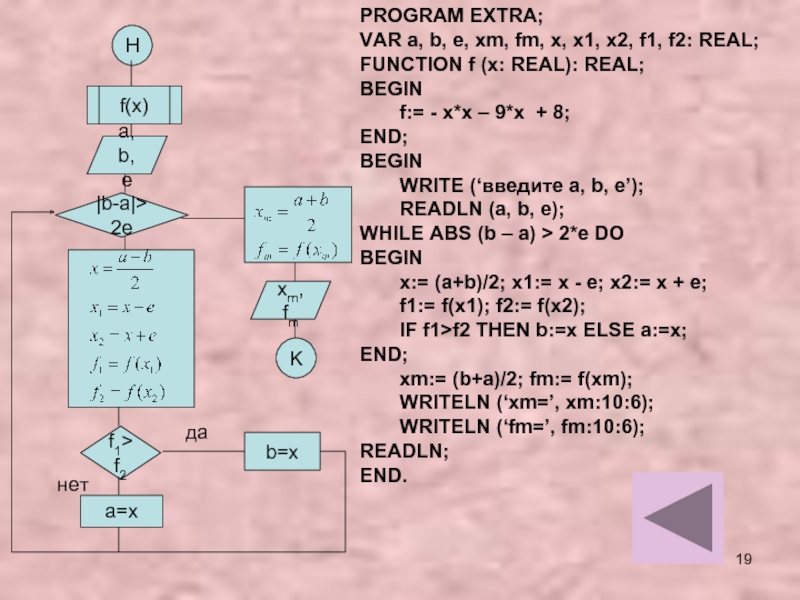
- 19. Нf(x)a, b, e|b-a|>2ef1>f2a=xxm, fmKb=xPROGRAM EXTRA;VAR a, b,
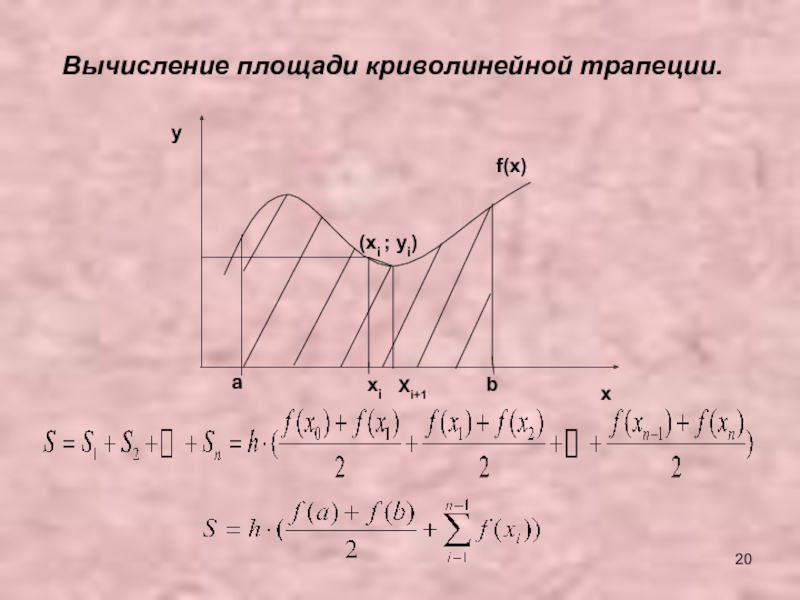
- 20. abxif(x)yx(xi ; yi)Вычисление площади криволинейной трапеции.Xi+1
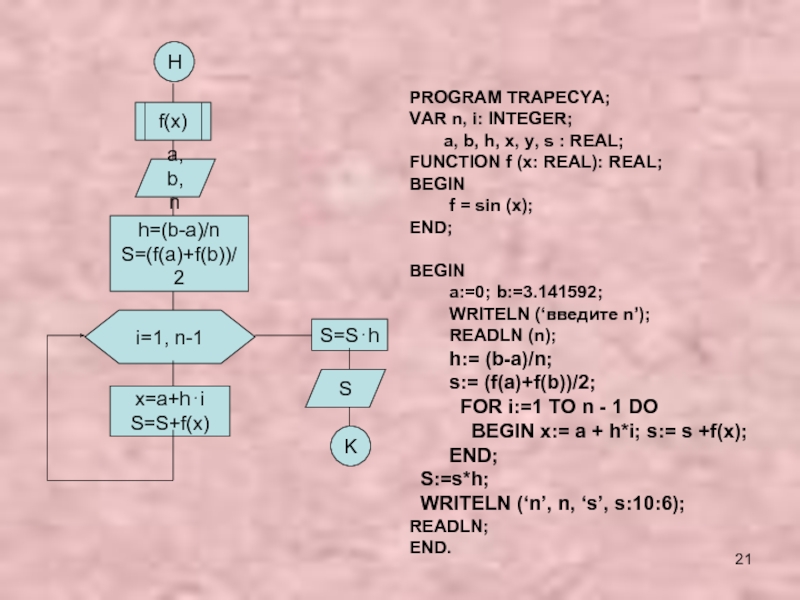
- 21. Hf(x)a, b, nh=(b-a)/nS=(f(a)+f(b))/2i=1, n-1x=a+h⋅iS=S+f(x)S=S⋅hSKPROGRAM TRAPECYA;VAR n, i:
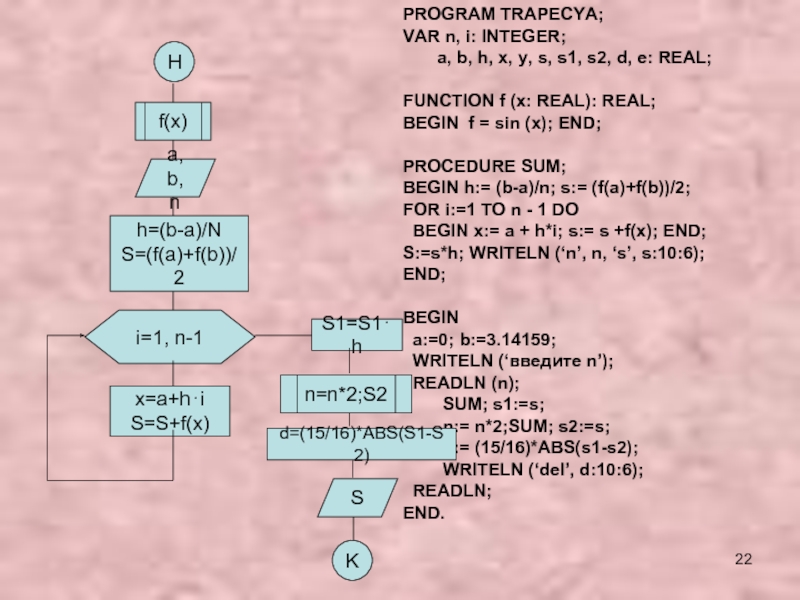
- 22. Hf(x)a, b, nh=(b-a)/NS=(f(a)+f(b))/2i=1, n-1x=a+h⋅iS=S+f(x)S1=S1⋅hSKPROGRAM TRAPECYA;VAR n, i:
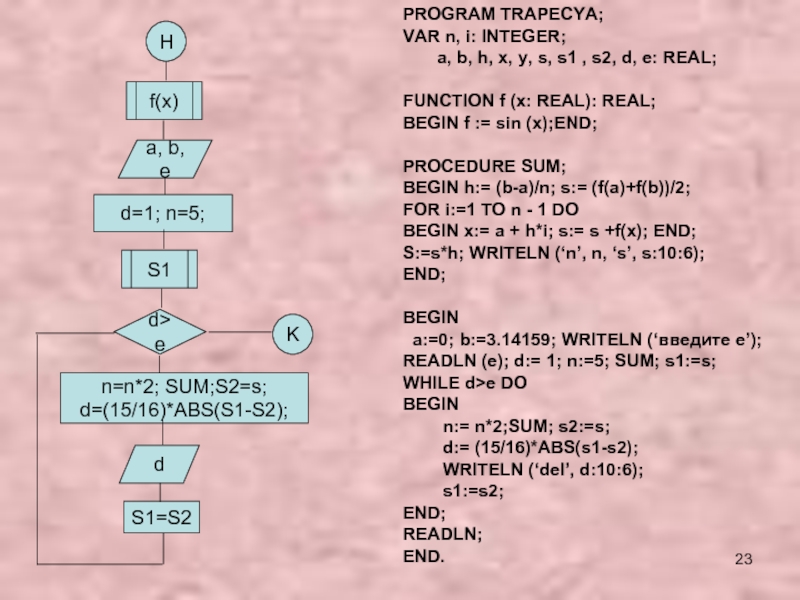
- 23. Hf(x)a, b, ed=1; n=5;n=n*2; SUM;S2=s; d=(15/16)*ABS(S1-S2);S1=S2dKPROGRAM TRAPECYA;VAR
- 24. Вычисление площади криволинейной трапеции с заданной точностью
- 25. Определение погрешности вычисления интеграла
- 26. Математическое моделирование с использованием ПК позволяет находить
- 27. Скачать презентанцию
Моделирование – это метод познания, состоящий в создании и исследовании моделей.Модель – это некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса.Один и тот же объект может иметь
Слайды и текст этой презентации
Слайд 2Моделирование – это метод познания, состоящий в создании и исследовании
моделей.
Модель – это некий новый объект, который отражает существенные особенности
изучаемого объекта, явления или процесса.Один и тот же объект может иметь множество моделей, а разные объекты могут описываться одной моделью.
Слайд 3Модели – упрощенное подобие реального объекта
Информационные модели
Натуральные модели
Формализация – замена
натурального объекта его моделью
Слайд 5Информационные модели
Табличная информационная модель
Иерархическая информационная модель
Сетевая информационная модель
Слайд 6
В табличной информационной модели перечень
однотипных объектов или свойств размещен в
первом
столбце (или строке) таблицы, а значения их свойств размещаются в следующих
столбцах (или строках) таблицы.
Слайд 7
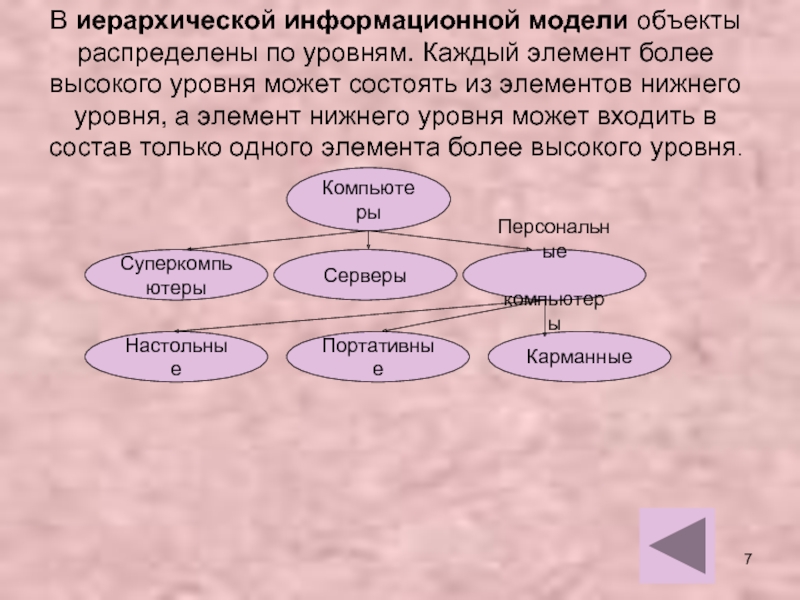
В иерархической информационной модели объекты
распределены по уровням. Каждый элемент более
высокого
уровня может состоять из элементов нижнего уровня, а элемент нижнего уровня
может входить в состав только одного элемента более высокого уровня.Компьютеры
Суперкомпьютеры
Серверы
Персональные
компьютеры
Настольные
Портативные
Карманные
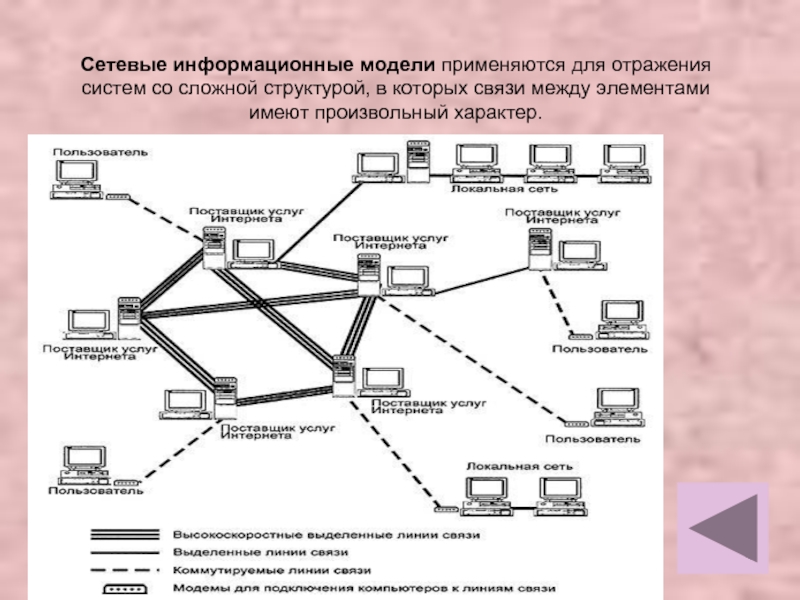
Слайд 8Сетевые информационные модели применяются для отражения систем со сложной структурой, в
которых связи между элементами
имеют произвольный характер.
Слайд 9
Модели, описывающие состояние системы в определенный момент времени, называются статическими
информационными моделями.
Модели, описывающие процессы изменения и развития систем, называются динамическими
информационными моделями.
Слайд 10С помощью формальных языков строятся формальные
информационные модели (математические, логические
и д.р.).
Одним из наиболее широко используемых
формальных языков является математика.
Формальные информационные
моделиМатематические модели
Логические модели
Слайд 12Математическая модель – это система математических соотношений –
формул, уравнений,
неравенств и т.д., отражающих существенные свойства
объекта или явления.
Слайд 13Основные этапы разработки и исследования моделей на компьютере.
Создание описательной информационной
модели.
Создание формализованной модели.
Преобразование формализованной модели в компьютерную модель.
Проведение компьютерного эксперимента.
Анализ
полученных результатов и коррекция исследуемой модели.
Слайд 14Математические модели:
Приближенное решение уравнений
Определение экстремума функции
Вычисление площади криволинейной трапеции
Слайд 16Н
a, b, e
f(x)
c= (a+b)/2
p=f(a)⋅f(c)
p>0
b=c
|b-a|>2e
X0=(a+b)/2
X0
К
a=c
да
нет
нет
PROGRAM KOREN;
VAR a, b, c, e, p,
x0: REAL;
FUNCTION f (x: REAL): REAL;
BEGIN
f:=cos(x)-x;
END;
BEGIN
WRITE (‘Введите a, b,
e’);READLN (a, b, e);
WHILE ABS (b-a) > 2*e DO
BEGIN
c:= (a+b)/2;
p:= f(a)*f(с);
IF p>0 THEN a:=с ELSE b:=c;
END;
x0:= (a+b)/2;
WRITELN (‘x0=’, x0:10:6);
READLN;
END.
Слайд 19Н
f(x)
a, b, e
|b-a|>2e
f1>f2
a=x
xm, fm
K
b=x
PROGRAM EXTRA;
VAR a, b, e, xm, fm,
x, x1, x2, f1, f2: REAL;
FUNCTION f (x: REAL): REAL;
BEGIN
f:=
- x*x – 9*x + 8;END;
BEGIN
WRITE (‘введите a, b, e’);
READLN (a, b, e);
WHILE ABS (b – a) > 2*e DO
BEGIN
x:= (a+b)/2; x1:= x - e; x2:= x + e;
f1:= f(x1); f2:= f(x2);
IF f1>f2 THEN b:=x ELSE a:=x;
END;
xm:= (b+a)/2; fm:= f(xm);
WRITELN (‘xm=’, xm:10:6);
WRITELN (‘fm=’, fm:10:6);
READLN;
END.
да
нет
Слайд 21H
f(x)
a, b, n
h=(b-a)/n
S=(f(a)+f(b))/2
i=1, n-1
x=a+h⋅i
S=S+f(x)
S=S⋅h
S
K
PROGRAM TRAPECYA;
VAR n, i: INTEGER;
a, b, h, x, y, s : REAL;
FUNCTION f
(x: REAL): REAL;BEGIN
f = sin (x);
END;
BEGIN
a:=0; b:=3.141592;
WRITELN (‘введите n’);
READLN (n);
h:= (b-a)/n;
s:= (f(a)+f(b))/2;
FOR i:=1 TO n - 1 DO
BEGIN x:= a + h*i; s:= s +f(x); END;
S:=s*h;
WRITELN (‘n’, n, ‘s’, s:10:6);
READLN;
END.
Слайд 22H
f(x)
a, b, n
h=(b-a)/N
S=(f(a)+f(b))/2
i=1, n-1
x=a+h⋅i
S=S+f(x)
S1=S1⋅h
S
K
PROGRAM TRAPECYA;
VAR n, i: INTEGER;
a, b, h, x, y, s, s1, s2, d,
e: REAL;FUNCTION f (x: REAL): REAL;
BEGIN f = sin (x); END;
PROCEDURE SUM;
BEGIN h:= (b-a)/n; s:= (f(a)+f(b))/2;
FOR i:=1 TO n - 1 DO
BEGIN x:= a + h*i; s:= s +f(x); END;
S:=s*h; WRITELN (‘n’, n, ‘s’, s:10:6);
END;
BEGIN
a:=0; b:=3.14159;
WRITELN (‘введите n’);
READLN (n);
SUM; s1:=s;
n:= n*2;SUM; s2:=s;
d:= (15/16)*ABS(s1-s2);
WRITELN (‘del’, d:10:6);
READLN;
END.
n=n*2;S2
d=(15/16)*ABS(S1-S2)
Слайд 23H
f(x)
a, b, e
d=1; n=5;
n=n*2; SUM;S2=s;
d=(15/16)*ABS(S1-S2);
S1=S2
d
K
PROGRAM TRAPECYA;
VAR n, i: INTEGER;
a, b, h, x, y, s, s1
, s2, d, e: REAL;FUNCTION f (x: REAL): REAL;
BEGIN f := sin (x);END;
PROCEDURE SUM;
BEGIN h:= (b-a)/n; s:= (f(a)+f(b))/2;
FOR i:=1 TO n - 1 DO
BEGIN x:= a + h*i; s:= s +f(x); END;
S:=s*h; WRITELN (‘n’, n, ‘s’, s:10:6);
END;
BEGIN
a:=0; b:=3.14159; WRITELN (‘введите e’);
READLN (e); d:= 1; n:=5; SUM; s1:=s;
WHILE d>e DO
BEGIN
n:= n*2;SUM; s2:=s;
d:= (15/16)*ABS(s1-s2);
WRITELN (‘del’, d:10:6);
s1:=s2;
END;
READLN;
END.
S1
d>e
Слайд 26Математическое моделирование с использованием ПК позволяет находить решения задач, которые
нельзя решить аналитически.
При использовании метода половинного деления при вычислении корня
функции и экстремума функции точность вычисления задается пользователем, что влияет на длительность вычислительного процесса.Для уменьшения погрешности вычислений площади криволинейной трапеции необходимо увеличивать количество отрезков разбиения.
Заданная точность вычисления площади криволинейной трапеции достигается многократным увеличением количества отрезков разбиения.
Выводы:
Теги
