Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы логики. Алгебра высказываний 10-11 класс
Содержание
- 1. Основы логики. Алгебра высказываний 10-11 класс
- 2. Алгебра высказываний Алгебра высказываний была разработана для того,
- 3. Логические переменныеЛогические переменные – простые высказывания, содержащие
- 4. Логические переменныеНапример, два простых высказывания:А = «2
- 5. В алгебре высказываний высказывания обозначаются именами логических
- 6. В алгебре высказываний над логическими переменными (над
- 7. Составные высказыванияВысказывания, состоящие из нескольких простых суждений
- 8. Логические операцииКонъюнкция (логическое умножение, «И»)Дизъюнкция
- 9. Объединение двух или нескольких высказываний в одно
- 10. Логическая функция, полученная в результате конъюнкции, истинна
- 11. Конъюнкция. Определите истинность логической функции«2 × 2
- 12. Запись конъюнкции на формальном языке алгебры высказыванийF(A,B)
- 13. Значение логической функции определяется по
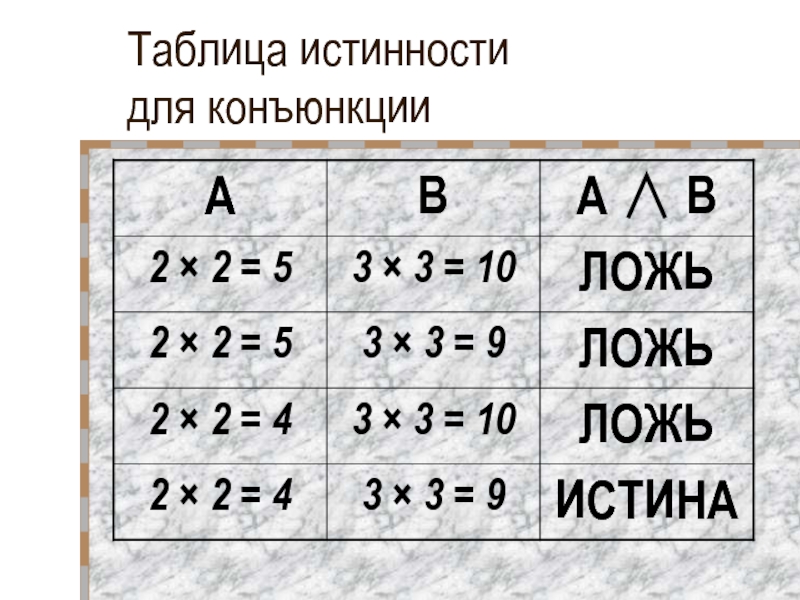
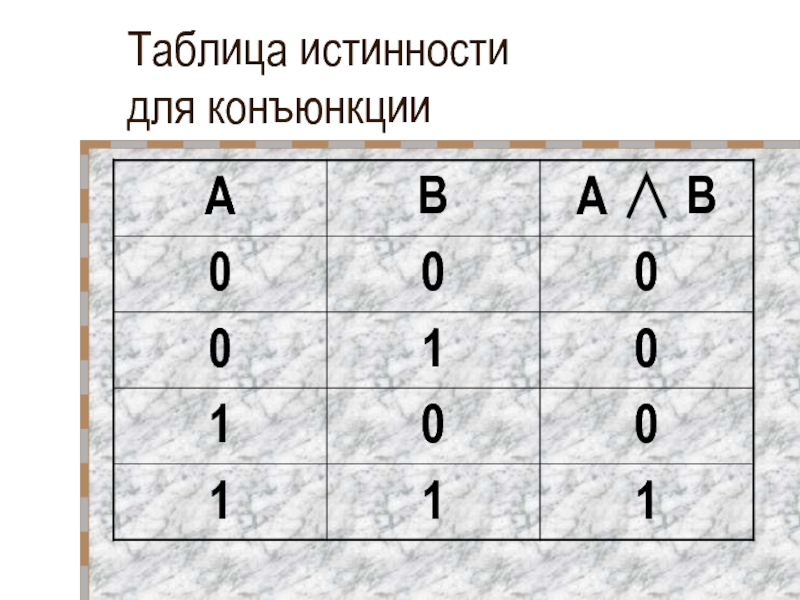
- 14. Таблица истинности для конъюнкции
- 15. Таблица истинности для конъюнкции
- 16. Объединение двух или нескольких высказываний в одно
- 17. Логическая функция, полученная в результате дизъюнкции, истинна
- 18. Дизъюнкция. Определите истинность логической функции«2 × 2
- 19. Запись дизъюнкции на формальном языке алгебры высказыванийF(A,B)
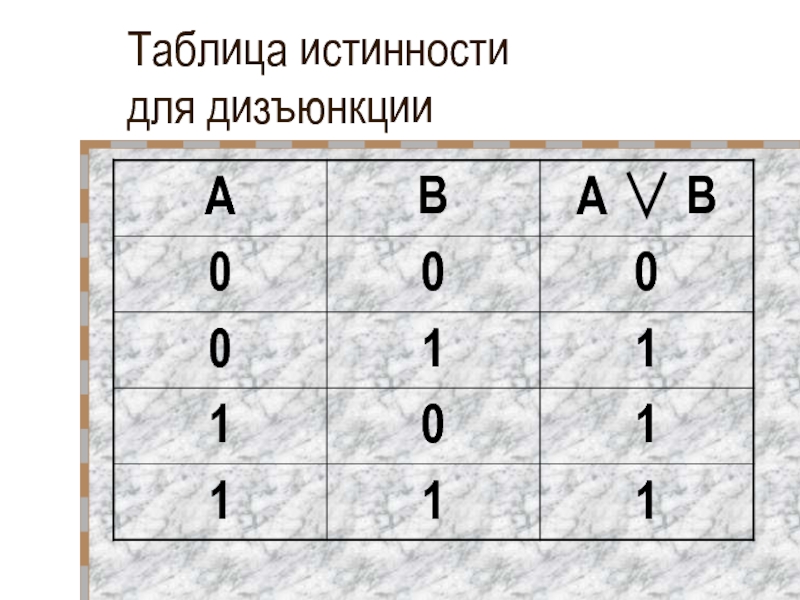
- 20. Таблица истинности для дизъюнкции
- 21. Таблица истинности для дизъюнкции
- 22. Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания, или инверсией
- 23. Логическое отрицание (инверсия) делает истинное высказывание ложным,
- 24. ИнверсияПусть A = «2 × 2 =
- 25. Запись инверсии на формальном языке алгебры высказыванийF(A)
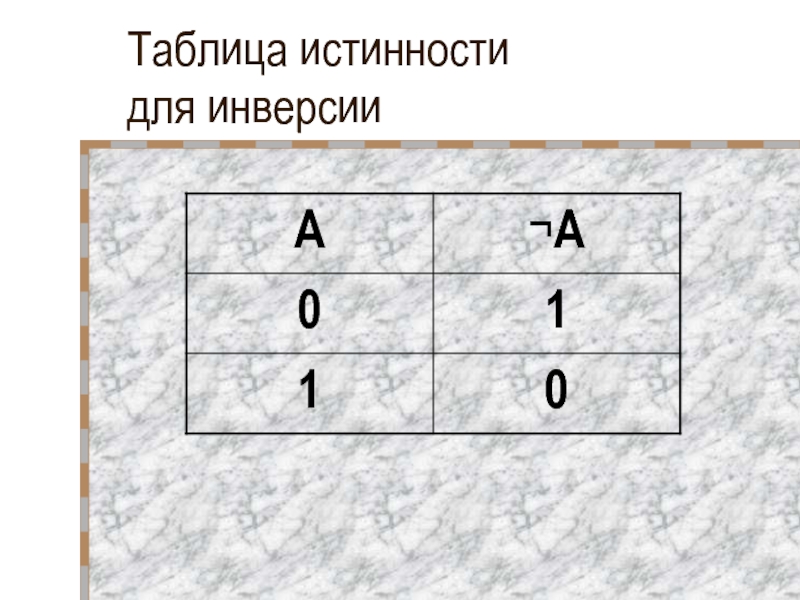
- 26. Таблица истинности для инверсии
- 27. Таблицы истинности основных логических функцийЛогическое умножениеA0011B0101A ∧ B0001Логическое сложениеЛогическое отрицаниеA01¬A10A0011B0101А ∨ В0111
- 28. Дополнительные логические функции Импликацию и эквивалентность
- 29. ИмпликацияОбъединение двух высказываний, из которых первое является
- 30. ИмпликацияИмпликация ложна тогда и только тогда,
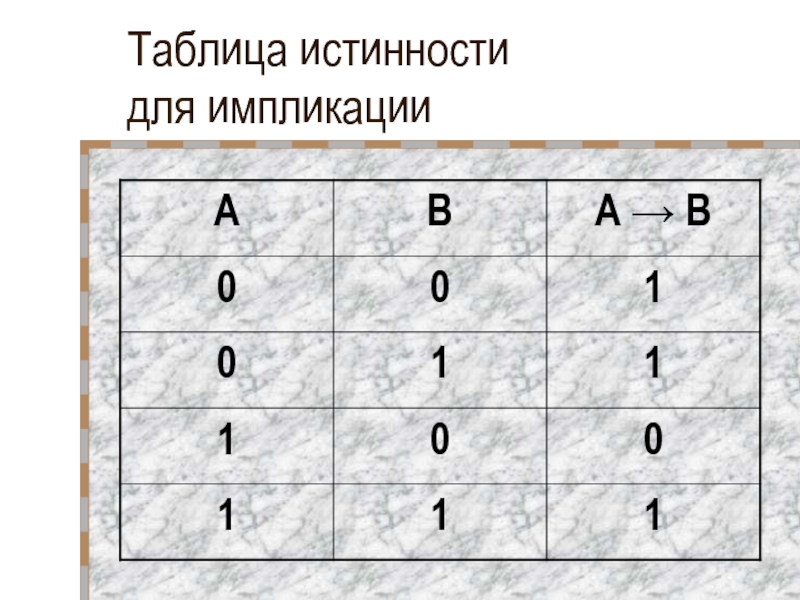
- 31. Таблица истинности для импликации
- 32. ЭквивалентностьЭквивалентность – это логическая операция, объединяющая два
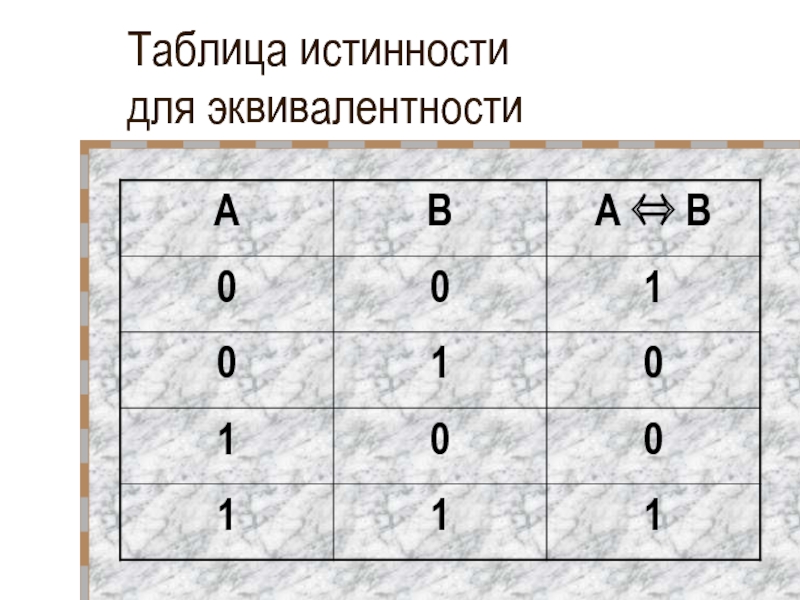
- 33. Таблица истинности для эквивалентности
- 34. ПереместительныйДизъюнкция: X ∨ Y ≡ Y ∨ XКонъюнкция: X ∧ Y ≡ Y ∧ XОсновные законы алгебры высказываний
- 35. СочетательныйДизъюнкция: X ∨ (Y ∨ Z) ≡ (X
- 36. РаспределительныйДизъюнкция: X ∧ (Y ∨ Z) ≡ X
- 37. Правила де МорганаДизъюнкция: ¬(X ∨ Y) ≡
- 38. ИдемпотенцииДизъюнкция: X ∨ X ≡ XКонъюнкция: X ∧ X ≡ XОсновные законы алгебры высказываний
- 39. ПоглощенияДизъюнкция: X ∨ (X ∧ Y) ≡
- 40. СклеиванияДизъюнкция: (X ∧ Y) ∨ (¬X ∧
- 41. Переменная со своей инверсиейДизъюнкция: X ∨
- 42. Операция с константамиДизъюнкция: X ∨ 0 ≡
- 43. Двойного отрицания ¬(¬X) ≡ XОсновные законы алгебры высказываний
- 44. Порядок действийДействия в скобкахОтрицаниеКонъюнкция ДизъюнкцияИмпликацияЭквивалентность
- 45. Скачать презентанцию
Алгебра высказываний Алгебра высказываний была разработана для того, чтобы определять истинность или ложность составных высказываний, не вникая в их содержание
Слайды и текст этой презентации
Слайд 1Основы логики
Алгебра высказываний
Автор:
Сергеев
Евгений Викторович
МОУ СОШ №4 г. Миньяра
Челябинской области
Слайд 2Алгебра высказываний
Алгебра высказываний была разработана для того, чтобы определять истинность
или ложность составных высказываний, не вникая в их содержание
Слайд 3Логические переменные
Логические переменные – простые высказывания, содержащие только одну мысль.
Обозначаются буквами латинского алфавита:
A, B, C…
Логические переменные могут принимать
лишь два значения: «ИСТИНА» (1) или «ЛОЖЬ» (0)
Слайд 4Логические переменные
Например, два простых высказывания:
А = «2 × 2 =
4» истина (1)
В = «2 × 2 = 5» ложь (0)
являются логическими переменными
А и В
Слайд 5
В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут
принимать лишь два значения:
«ИСТИНА» (1) или «ЛОЖЬ» (0)
Слайд 6
В алгебре высказываний над логическими переменными (над высказываниями) можно производить
определенные логические операции, в результате которых получаются новые высказывания
Слайд 7Составные высказывания
Высказывания, состоящие из нескольких простых суждений и содержащие в
себе более, чем одну простую мысль, называются логическими функциями
Обозначаются F(A,B,C…)
Также
могут принимать значения «ИСТИНА» или «ЛОЖЬ» в зависимости от того, какие значения имеют входящие в их состав логические переменные и от действий над ними
Слайд 8Логические операции
Конъюнкция
(логическое умножение, «И»)
Дизъюнкция
(логическое сложение, «ИЛИ»)
Инверсия
(логическое отрицание,
«НЕ»)
Импликация
(логическое следование, «Если А, то В»)
Эквивалентность
(логическое равенство, «А
тогда и только тогда, когда В»)
Слайд 9
Объединение двух или нескольких высказываний в одно с помощью союза
«И» называется операцией логического умножения, или конъюнкцией
Слайд 10
Логическая функция, полученная в результате конъюнкции, истинна тогда и только
тогда, когда истинны все входящие в него логические переменные
Слайд 11Конъюнкция. Определите истинность логической функции
«2 × 2 = 5» И
«3 × 3 = 10»
«2 × 2 = 5» И
«3 × 3 = 9»«2 × 2 = 4» И «3 × 3 = 10»
«2 × 2 = 4» И «3 × 3 = 9»
Истинна только функция (4)
Слайд 12Запись конъюнкции на формальном языке алгебры высказываний
F(A,B) = A &
B
или
F(A,B) = A ∧ B
Также может встретиться запись,
типа:F(A,B) = A * B
или
F(A,B) = A and B
Слайд 13Значение логической
функции определяется
по ее таблице истинности
Таблица истинности показывает
какие значения принимает логическая функция при всех возможных значениях логических
переменных
Слайд 16
Объединение двух или нескольких высказываний в одно с помощью союза
«ИЛИ» называется операцией логического сложения, или дизъюнкцией
Слайд 17
Логическая функция, полученная в результате дизъюнкции, истинна тогда, когда истинна
хотя бы одна из входящих в него логических переменных
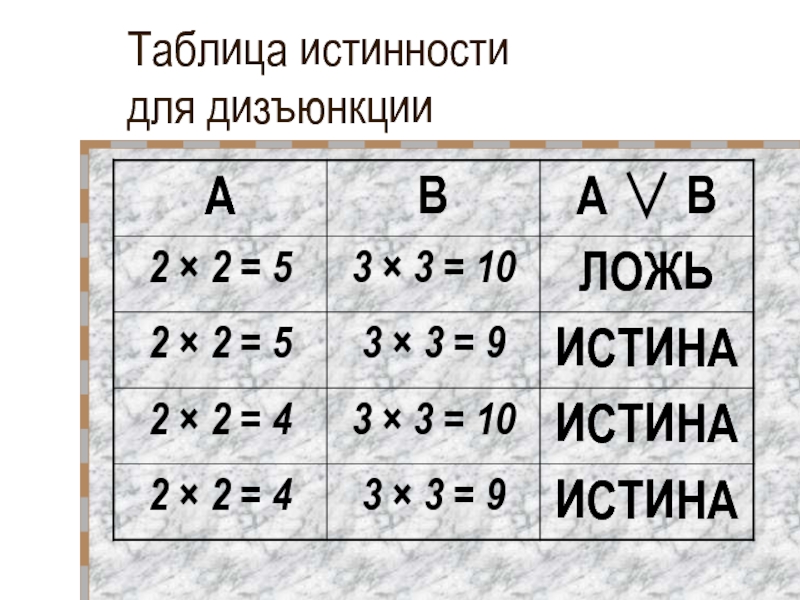
Слайд 18Дизъюнкция. Определите истинность логической функции
«2 × 2 = 5» ИЛИ
«3 × 3 = 10»
«2 × 2 = 5» ИЛИ
«3 × 3 = 9»«2 × 2 = 4» ИЛИ «3 × 3 = 10»
«2 × 2 = 4» ИЛИ «3 × 3 = 9»
Ложна только функция (1), остальные истинны
Слайд 19Запись дизъюнкции на формальном языке алгебры высказываний
F(A,B) = A ∨
B
Также может встретиться запись, типа:
F(A,B) = A + B
или
F(A,B)
= A or B
Слайд 22
Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания, или
инверсией
Слайд 23
Логическое отрицание (инверсия) делает истинное высказывание ложным, а ложное –
истинным
[логическая отрицательная
единица, перевертыш]
Слайд 24Инверсия
Пусть
A = «2 × 2 = 4»
– истинное высказывание,
тогда
F(A) = «2 × 2 ≠ 4»
– ложное высказывание
Слайд 25Запись инверсии на формальном языке алгебры высказываний
F(A) = ¬A
или
F(A) =
Ā
Также может встретиться запись, типа:
F(A) = not А
Слайд 27Таблицы истинности
основных логических функций
Логическое умножение
A
0
0
1
1
B
0
1
0
1
A ∧ B
0
0
0
1
Логическое сложение
Логическое отрицание
A
0
1
¬A
1
0
A
0
0
1
1
B
0
1
0
1
А
∨ В
0
1
1
1
Слайд 28Дополнительные
логические функции
Импликацию и эквивалентность можно выразить через конъюнкцию,
дизъюнкцию и отрицание, поэтому их называют дополнительными логическими функциями:
Импликация:
А →
В = ¬A ∨ В или А ⊃ В = ¬A ∨ В или
А ⇒ В = ¬A ∨ В
Эквивалентность:
А ↔ В = (¬A ∨ В) ∧ (¬B ∨ A) или
А ⇔ В = (¬A ∨ В) ∧ (¬B ∨ A) или
А ≡ В = (¬A ∨ В) ∧ (¬B ∨ A)
Слайд 29Импликация
Объединение двух высказываний, из которых первое является условием, а второе
– следствием из него, называется импликацией (логическим следованием)
Слайд 30Импликация
Импликация ложна
тогда и только тогда, когда
условие истинно,
а
следствие ложно
Пример:
Если выучишь материал, то сдашь зачет
Это высказывание
ложно только тогда, когда материал выучен, а зачет не сдан, т.к. сдать зачет можно и случайно, например если попался единственный знакомый вопрос или удалось воспользоваться шпаргалкой
Слайд 32Эквивалентность
Эквивалентность – это логическая операция, объединяющая два простых высказывания в
одно составное и которое является истинным тогда и только тогда, когда оба
исходных высказывания одновременно либо истинны, либо ложны.
Слайд 34Переместительный
Дизъюнкция:
X ∨ Y ≡ Y ∨ X
Конъюнкция:
X ∧ Y ≡
Y ∧ X
Основные законы алгебры высказываний
Слайд 35Сочетательный
Дизъюнкция:
X ∨ (Y ∨ Z) ≡ (X ∨ Y) ∨
Z
Конъюнкция:
X ∧ (Y ∧ Z) ≡ (X ∧ Y) ∧
ZОсновные законы алгебры высказываний
Слайд 36Распределительный
Дизъюнкция:
X ∧ (Y ∨ Z) ≡ X ∧ Y ∨
X ∧ Z
Конъюнкция:
X ∨ (Y ∧ Z) ≡ (X
∨ Y) ∧ (X ∨ Z)Основные законы алгебры высказываний
Слайд 37Правила де Моргана
Дизъюнкция:
¬(X ∨ Y) ≡ ¬X ∧ ¬Y
Конъюнкция:
¬(X ∧ Y) ≡ ¬X ∨ ¬Y
Основные законы алгебры высказываний
Слайд 39Поглощения
Дизъюнкция:
X ∨ (X ∧ Y) ≡ X
Конъюнкция:
X ∧
(X ∨ Y) ≡ X
Основные законы алгебры высказываний
Слайд 40Склеивания
Дизъюнкция:
(X ∧ Y) ∨ (¬X ∧ Y) ≡ Y
Конъюнкция:
(X ∨ Y) ∧ (¬X ∨ Y) ≡ Y
Основные законы
алгебры высказываний
Слайд 41Переменная
со своей инверсией
Дизъюнкция:
X ∨ ¬X ≡ 1
Конъюнкция:
X
∧ ¬X ≡ 0
Основные законы алгебры высказываний
Слайд 42Операция с константами
Дизъюнкция:
X ∨ 0 ≡ X, X ∨
1 ≡ 1
Конъюнкция:
X ∧ 0 ≡ 0, X ∧
1 ≡ XОсновные законы алгебры высказываний
