Основы логики(практика)

И.В.

– столица Франции. Сформулировать на обычном языке высказывания: A =

¬S; B = x & s; C=sx; D = s  ¬ x; M = x s. Определить их истинность.
Пусть n=1, m=0. Определить истинность высказывания

Построить таблицу истинности выражений:

 B) & (¬ A  ¬ B).
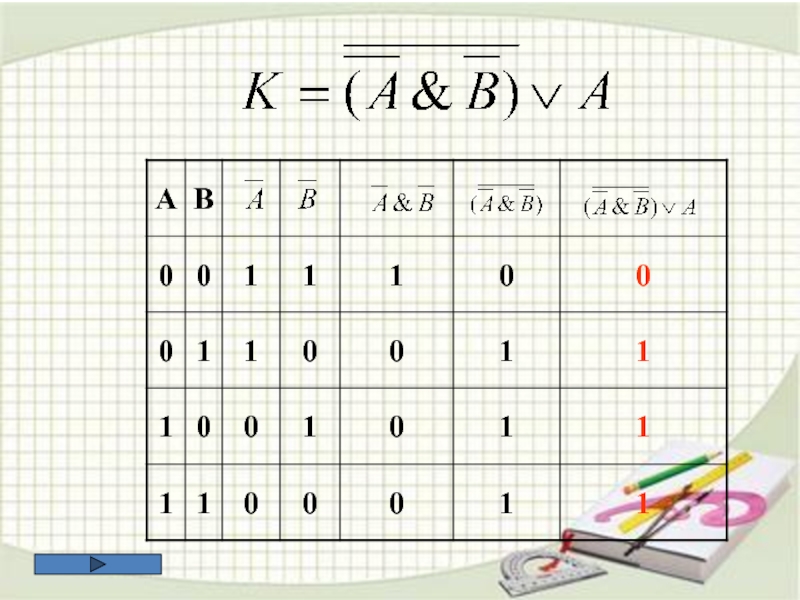
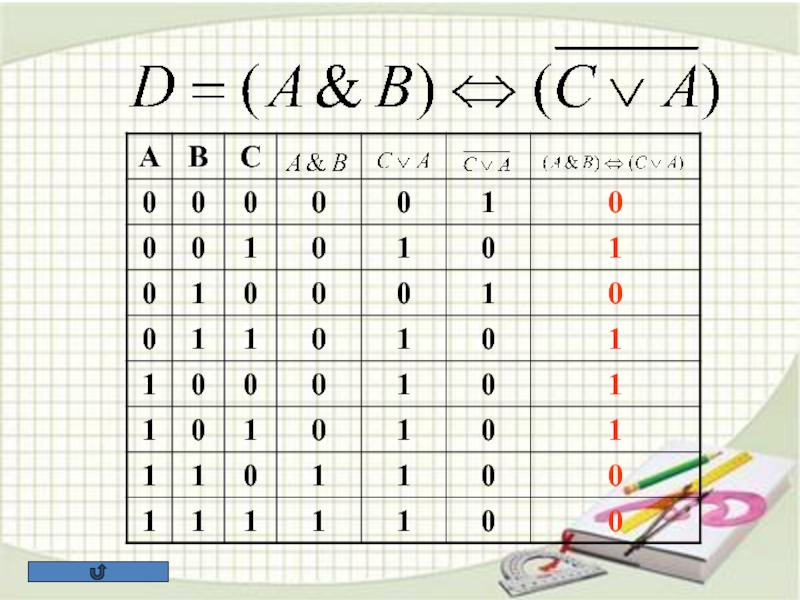
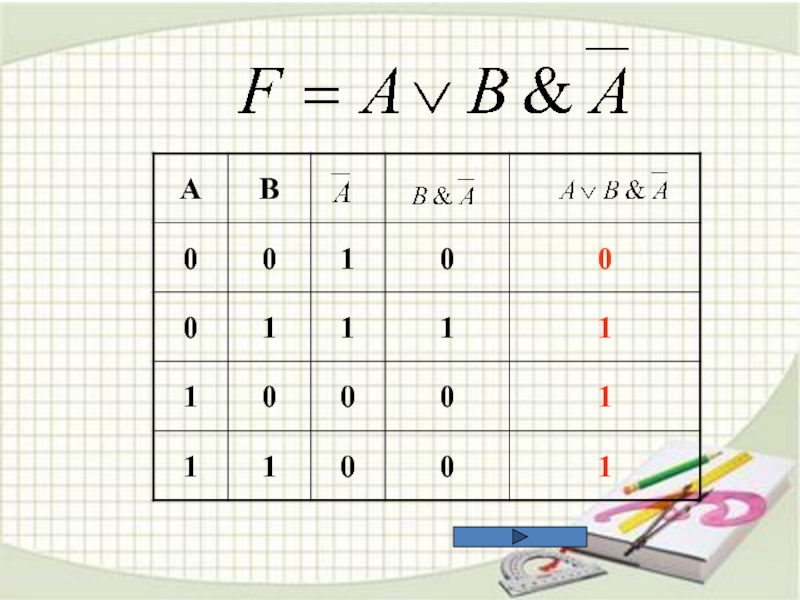
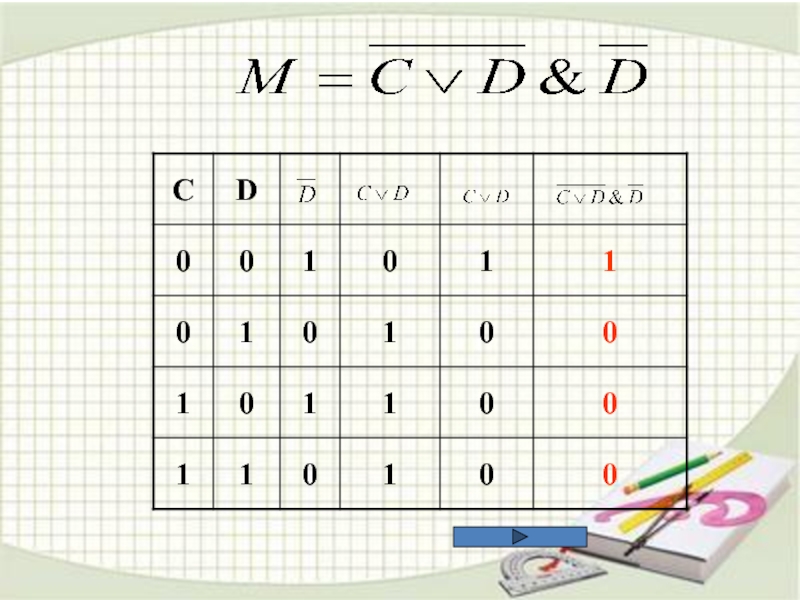
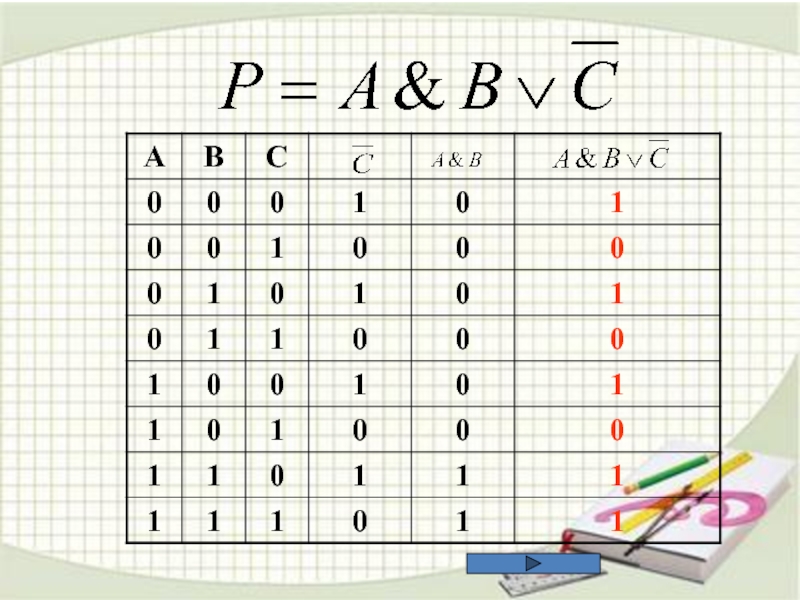
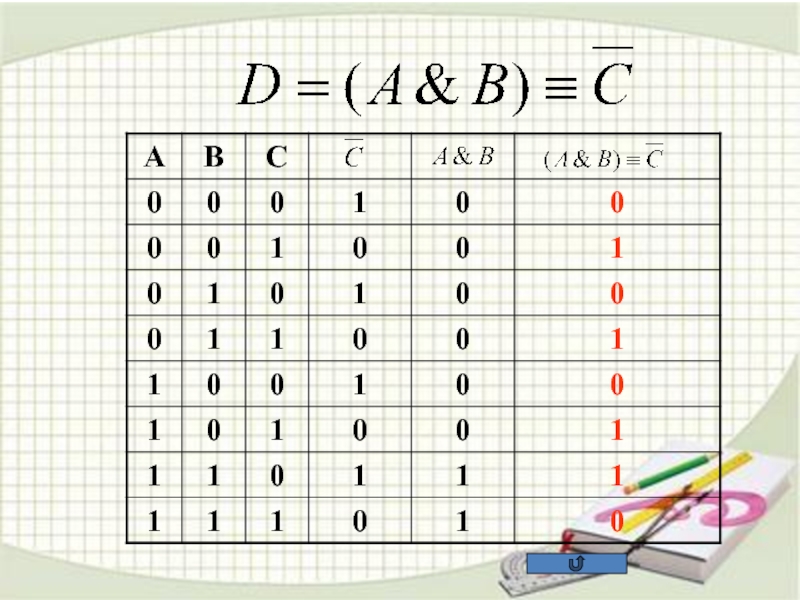
5. Построить таблицу

истинности следующих выражений:

6. ЗАДАЧИ ЕГЭ ПО ИНФОРМАТИКЕ

А3

А10

В15

столица Франции, а число 3 является делителем числа 198. (ложь).
Число

3 является делителем числа 198, или Иркутск – столица Франции. (истина).
Если число 3 является делителем числа 198, то Иркутск – не столица Франции. (истина).
Иркутск – столица Франции тогда и только тогда, когда число 3 является делителем числа 198. (ложь)

∨ x2 ∨ x3 ∨ ¬x4 ∨ ¬x5 2) ¬x1 ∨

x2 ∨ ¬x3 ∨ x4 ∨ ¬x5 3) x1 ∧ ¬x2 ∧ x3 ∧ ¬x4 ∧ x5 4) ¬x1 ∧ x2 ∧ x3 ∧ x4 ∧ ¬x5

По­яс­не­ние.

По­смот­рим вни­ма­тель­но на от­ве­ты. Они пред­став­ля­ют собой либо конъ­юнк­цию, либо дизъ­юнк­цию дан­ных пяти пе­ре­мен­ных или от­ри­ца­тель­ных к ним.
Сна­ча­ла вы­яс­ним, конъ­юнк­ция это или дизъ­юнк­ция.
 Дизъ­юнк­ция не может при­ни­мать зна­че­ние ноля два­жды из трех раз­ных ком­би­на­ций, сле­до­ва­тель­но, в от­ве­те долж­на быть конъ­юнк­ция. Вы­чер­ки­ва­ем 1 и 2 ва­ри­ан­ты от­ве­та.
Из 3 и 4 ва­ри­ан­тов под­хо­дит 4. Пра­виль­ный ответ - 4.

ЗАДАЧА А3

x4, x5, y1, y2, y3, y4, y5, ко­то­рые удо­вле­тво­ря­ют всем

пе­ре­чис­лен­ным ниже усло­ви­ям? 
(x1 → x2) ∧ (x2 → x3) ∧ (x3 → x4) ∧ (x4 → x5 ) = 1
(y1 → y2) ∧ (y2 → y3) ∧ (y3 → y4) ∧ (y4 → y5 ) = 1
x1 ∨ y1 = 1
 В от­ве­те не нужно пе­ре­чис­лять все раз­лич­ные на­бо­ры зна­че­ний пе­ре­мен­ных x1, x2, x3, x4, x5, y1, y2, y3, y4, y5, при ко­то­рых вы­пол­не­на дан­ная си­сте­ма ра­венств. В ка­че­стве от­ве­та Вам нужно ука­зать ко­ли­че­ство таких на­бо­ров.

По­яс­не­ние.

1) Из по­след­не­го урав­не­ния сле­ду­ет, что гло­баль­но мы имеем три ва­ри­ан­та - x1=1, y1=1; x1=0, y1=1; x1=1, y1=0.
2) Ло­ги­че­ское И ис­тин­но, толь­ко тогда, когда ис­ти­ны все утвер­жде­ния, а им­пли­ка­ция ложна толь­ко в слу­чае, если из ис­тин­но­го сле­ду­ет лож­ное.
3) Урав­не­ние (1) опи­сы­ва­ет ряд пе­ре­мен­ных {x1, x2, x3, x4, x5}. Так как из пе­ре­мен­ной с более низ­ким но­ме­ром все­гда сле­ду­ет пе­ре­мен­ная с более вы­со­ким, если любую пе­ре­мен­ную из этого ряда при­рав­нять 1, то все сле­ду­ю­щие долж­ны также быть равны 1. Для урав­не­ния (2) су­ще­ству­ет то же самое пра­ви­ло. Иначе го­во­ря, если за­пи­сать пе­ре­мен­ные x (или y) в по­ряд­ке воз­рас­та­ния их но­ме­ров, слева будут нули, а спра­ва - еди­ни­цы.
4) Рас­смот­рим ва­ри­ант x1=1, y1=1. Так как пер­вые числа каж­до­го ряда равны 1, то все сле­ду­ю­щие тоже равны 1. Су­ще­ству­ет толь­ко одна ком­би­на­ция для этого ва­ри­ан­та.
5) Рас­смот­рим ва­ри­ант x1=0, y1=1. Для y-ряда все пе­ре­мен­ные равны 1, для x же су­ще­ству­ет 5 ком­би­на­ций, так как в ряде x может быть от 1 до 5 нолей вклю­чи­тель­но.
6) По­след­ний ва­ри­ант рас­смот­рим ана­ло­гич­но преды­ду­ще­му. Там су­ще­ству­ет всего 5 ком­би­на­ций.
 
Пра­виль­ный ответ: 5+5+1=11 ком­би­на­ций.

ЗАДАЧА В15

такой отрезок A, что формула ((x∈А)→¬(x∈Q))∨(x∈P) тождественно истинна, то есть

принимает значение 1 при любом значении переменной х.
1.[4;34]
2. [4;24]
3. [4;14]
4. [14;24]

По­яс­не­ние.

Преобразуем выражение – заменим импликацию дизъюнкцией. Получим: (¬(x∈А))∨(¬(x∈Q))∨(x∈P) Выражение (¬(x∈Q))∨(x∈P) истинно для тех только тех x, которые либо лежат в P, либо не лежат в Q, иными словами – для x∈R, где R=(−∞,15]∪(21,+∞). Выражение (¬(x∈A))∨(x∈R) тождественно истинно тогда и только тогда, когда A⊆R. Этому условию удовлетворяет только отрезок [4,14].

ЗАДАЧА А10