Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация для урока "Метод координат"
Содержание
- 1. Презентация для урока "Метод координат"
- 2. П О В Т О Р Е Н И Е
- 3. Задание на смекалкуВ этой таблице спрятаны обрывки
- 4. Слайд 4
- 5. Слайд 5
- 6. Формы представления информации.
- 7. Форма знаковзрительные знакислуховые знакиосязательные знакиобонятельные знакивкусовые знаки1!Для
- 8. Значение знаковИконические знакиСимволы +-Н:-)Позволяют догадаться об их
- 9. Естественные языки- это такие знаковые системы, которые
- 10. Формальные языки- это такие знаковые системы, в
- 11. Шифрование Существуют до сих пор не расшифрованные
- 12. – это «азбука» хранения и передачи наследственной информации живыми организмамиГенетический алфавит
- 13. Двоичная знаковая системаиспользуется в процессах хранения, обработки
- 14. «Лучше один раз увидеть,чем сто раз услышать»,-гласит
- 15. ?(3,1), (6,3), (4,2), (5,1), (5,3)(1,1), (5,1), (5,1), (2,2), (5,3), (10,3), (4,1), (1,3), (4,2)
- 16. Рене Декарт – французский математик, физик, физиолог
- 17. !Метод координат – это один из удобных способов представления графической информации с помощью чисел.
- 18. Луч Ох с началом отсчета в точке О, на котором
- 19. Метод координатНарисуем в тетради две перпендикулярные оси, точку пересечения обозначим через О:
- 20. Метод координатГоризонтальная ось называется осью OX,а вертикальная
- 21. Метод координатКаждая точка на координатной плоскости имеет
- 22. ОYX
- 23. Ежедневно делайте зарядку для глаз
- 24. Метод координатВ жизни мы часто встречаемся с
- 25. ОYX
- 26. Слайд 26
- 27. Метод координатВ качестве примера давайте рассмотрим построение
- 28. Внимание!
- 29. Задание 1. Заполни пропуски
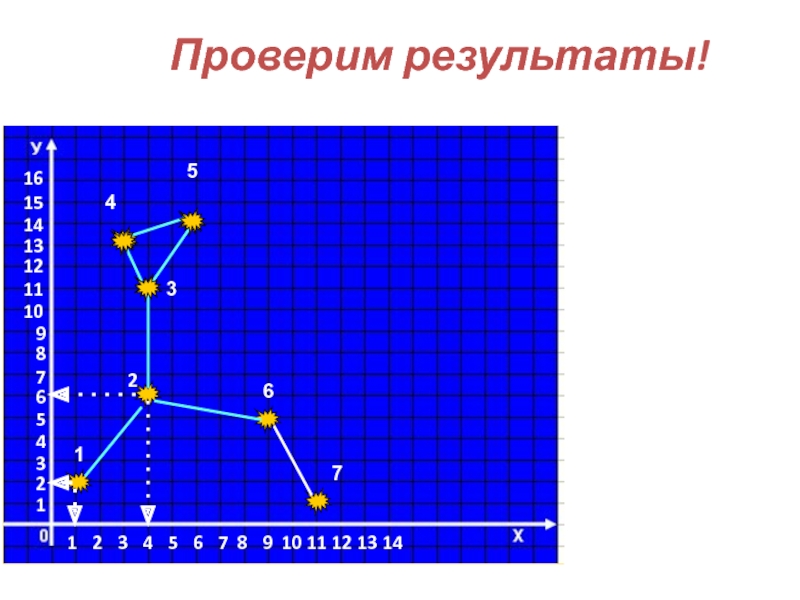
- 30. Проверим результаты!1612345678910111211123456789101213141234567131415
- 31. Внимание!
- 32. Слайд 32
- 33. festival.1september.ruvideouroki.netmetod-kopilka.rupomochnik-vsem.ruru.wikipedia.orgПолезные ссылки
- 34. Скачать презентанцию
П О В Т О Р Е Н И Е
Слайды и текст этой презентации
Слайд 1Тема урока «Формы представления информации. Метод координат»
Учитель информатики
МБОУ СОШ№9
Разетдинова Альбина
Фаритовна
Слайд 3Задание на смекалку
В этой таблице спрятаны обрывки записок
Зайца (А2,
Г6, Г1, А6, В3, Б1, Г4, Б4);
Волка (А3, Г2,
Б3, Г5, Б2, Б6, В2, В6);для тебя (В5, А1, Г3, А4, В1).
Восстанови эти записки (не забудь разделить текст на слова).
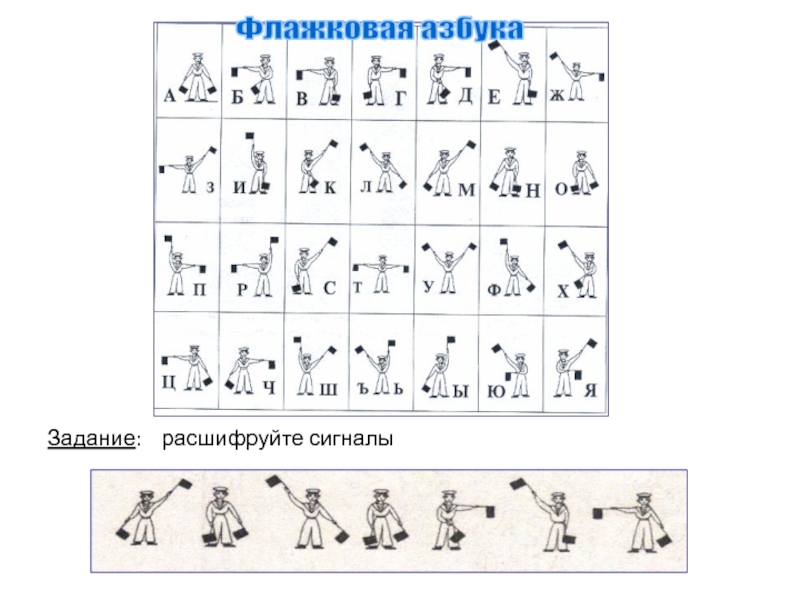
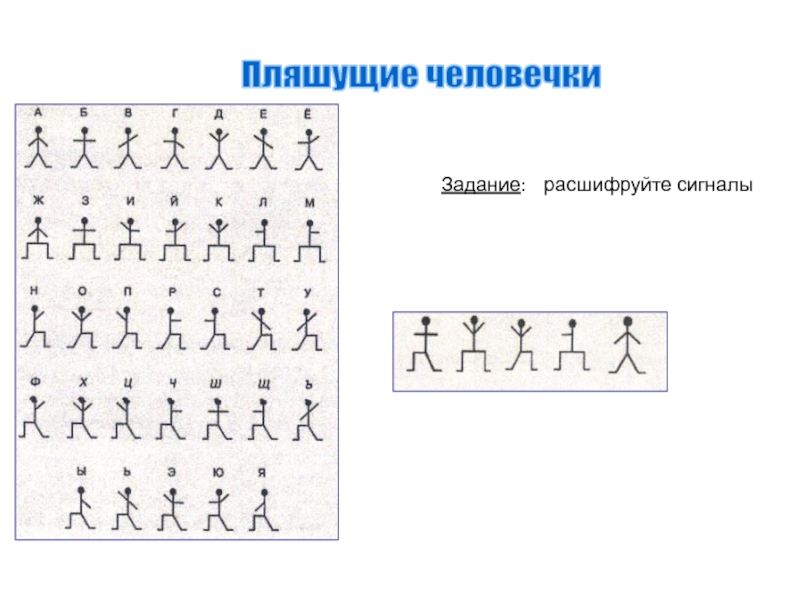
Слайд 7Форма знаков
зрительные знаки
слуховые знаки
осязательные знаки
обонятельные знаки
вкусовые знаки
1
!
Для передачи информации на
большие расстояния используются знаки в форме сигналов
Слайд 8Значение знаков
Иконические знаки
Символы
+
-
Н
:-)
Позволяют догадаться об их смысле, т.к. по
форме напоминают сам объект
Это знаки, для которых связь между формой
и значением устанавливается соглашением
Слайд 9Естественные языки
- это такие знаковые системы, которые человек использует в
целях обмена информацией
немецкий
русский
английский
китайский
французский
и другие (более сотни) языков
испанский
Слайд 10Формальные языки
- это такие знаковые системы, в которых существует ограниченное
количество строгих правил грамматики и синтаксиса и однозначная запись знаками
смысла сообщенийДесятичная система счисления
Язык программирования
Язык химических элементов
Язык музыкальных нот
Язык дорожных знаков
Язык электрических схем
и другие
Слайд 11Шифрование
Существуют до сих пор не расшифрованные тексты на древних
языках
Знак «О»
Буква «О» в русском алфавите
Буква «О» (ou) в английском
алфавитеЦифра «0» (ноль) в системах счисления
Символ химического элемента «О» кислорода в таблице Менделеева
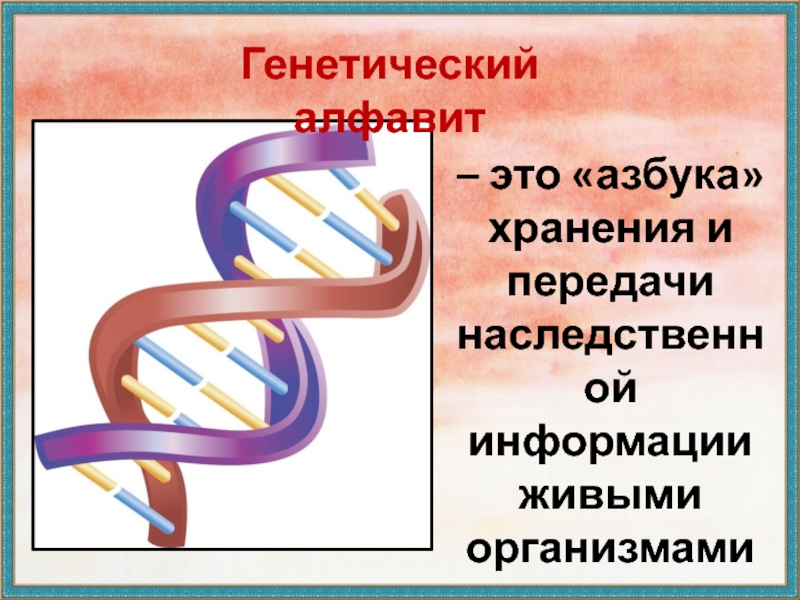
Слайд 12– это «азбука» хранения и передачи наследственной информации живыми организмами
Генетический
алфавит
Слайд 13Двоичная знаковая система
используется в процессах хранения, обработки и передачи информации
в компьютере
0 – нет импульса
1 – есть импульс
Слайд 14«Лучше один раз увидеть,чем сто раз услышать»,-гласит народная мудрость. Любая информация
может быть представлена с помощью чисел. Чтобы «связать» числа и точки,используют
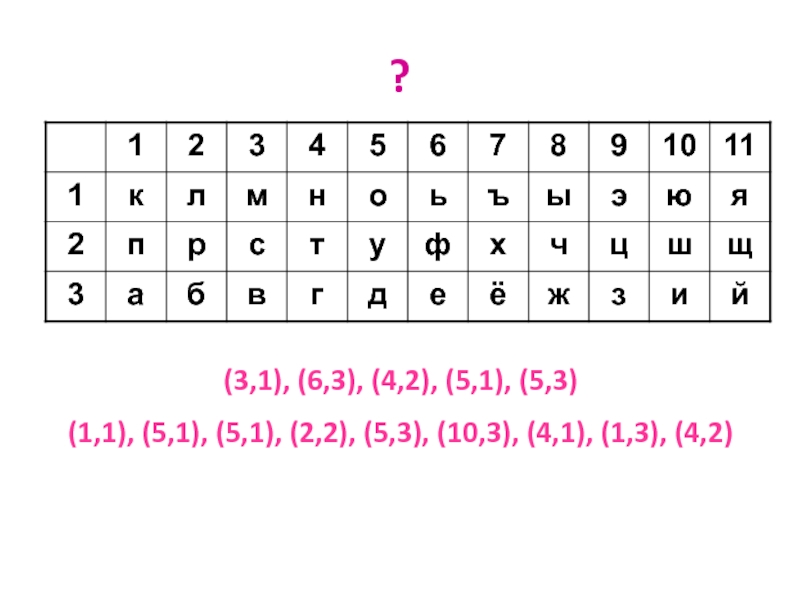
системы координат.
Слайд 15?
(3,1), (6,3), (4,2), (5,1), (5,3)
(1,1), (5,1), (5,1), (2,2), (5,3), (10,3),
(4,1), (1,3), (4,2)
Слайд 16Рене Декарт – французский математик, физик, физиолог и философ, создатель
знаменитого метода координат, сторонник аналитического метода в математике.
Слайд 17!
Метод координат – это один из удобных способов представления графической
информации с помощью чисел.
Слайд 18Луч Ох с началом отсчета в точке О, на котором указаны единичный отрезок и направление,
называют координатным лучом.
Число, соответствующее точке координатного луча, называется координатой этой точки. Например,
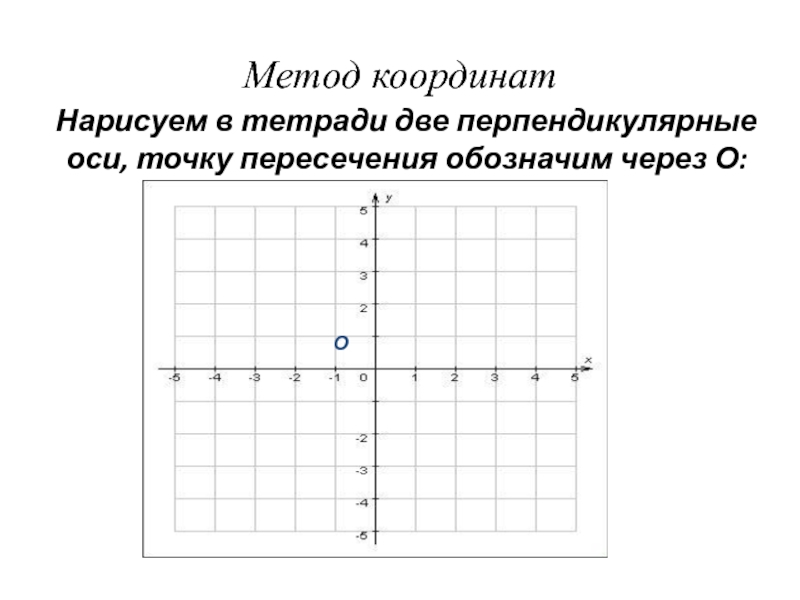
А(4). Читают: точка А с координатой 4.
Слайд 19Метод координат
Нарисуем в тетради две перпендикулярные оси, точку пересечения обозначим
через О:
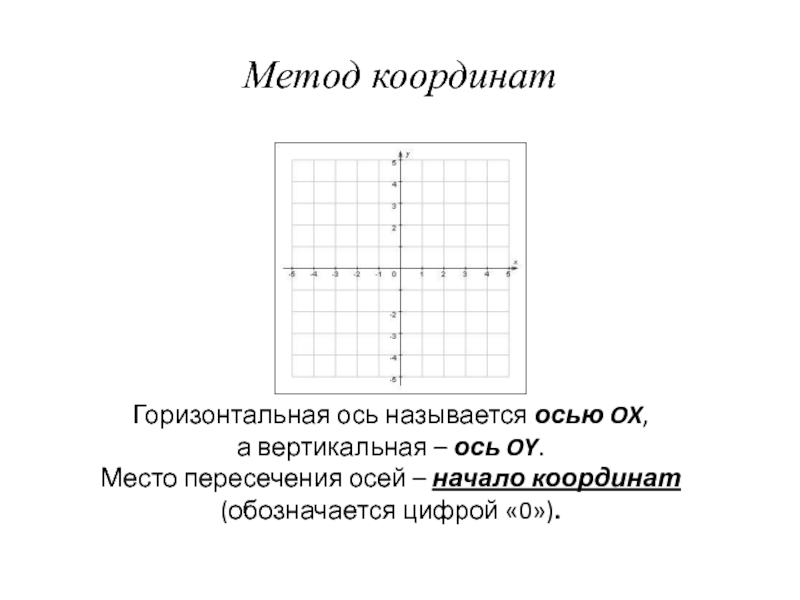
Слайд 20Метод координат
Горизонтальная ось называется осью OX,
а вертикальная – ось OY.
Место пересечения осей – начало координат (обозначается цифрой «0»).
Слайд 21Метод координат
Каждая точка на координатной плоскости
имеет свой адрес.
Это
пара чисел: первое число по оси OX,
второе – по
оси OY.Эти числа называются координатами точки.
Правила записи координат точки:
Координаты точки записываются в круглых скобках через «;».
На первом месте записывается координата по оси OX, на втором – оси OY.
Например: координаты точки А изображенной на данном чертеже будут записаны следующим образом:
А (4; 3)
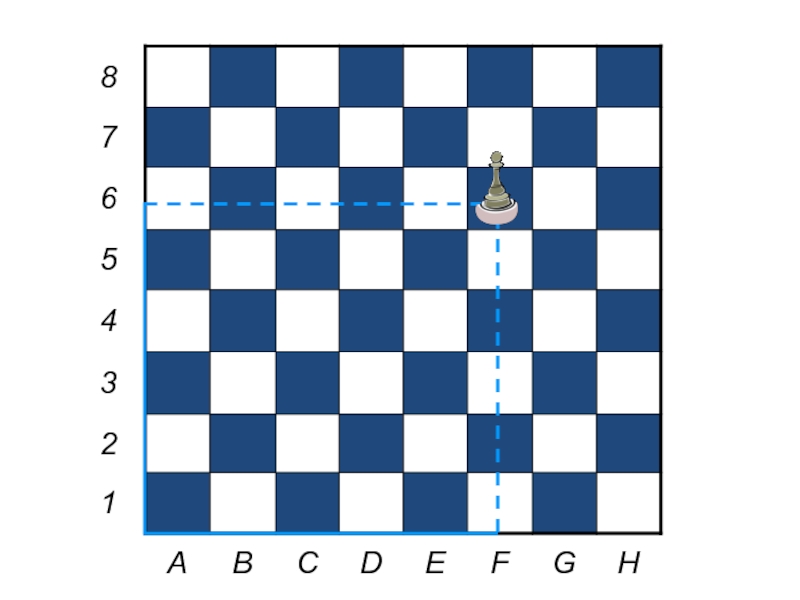
Слайд 24Метод координат
В жизни мы часто встречаемся с подобной системой (шахматная
доска, зрительный зал, местонахождение парты в классе)
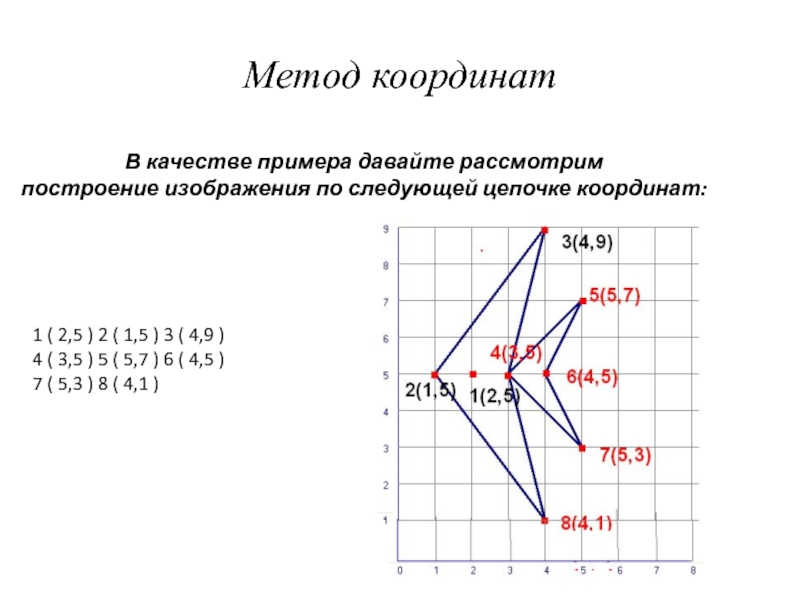
Слайд 27Метод координат
В качестве примера давайте рассмотрим
построение изображения по следующей
цепочке координат:
1 ( 2,5 ) 2 ( 1,5 ) 3
( 4,9 ) 4 ( 3,5 ) 5 ( 5,7 ) 6 ( 4,5 )
7 ( 5,3 ) 8 ( 4,1 )
Слайд 33festival.1september.ru
videouroki.net
metod-kopilka.ru
pomochnik-vsem.ru
ru.wikipedia.org
Полезные ссылки
