Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация к уроку информатики: "Вычисление определителей".
Содержание
- 1. Презентация к уроку информатики: "Вычисление определителей".
- 2. Матрицы— это прямоугольные таблицы из чисел, содержащие
- 3. Ма́трица— математический объект, записываемый в виде прямоугольной
- 4. Матрицы допускают следующие алгебраические операции:сложение матриц, имеющих
- 5. Матрицы записываются с помощью больших круглых скобок
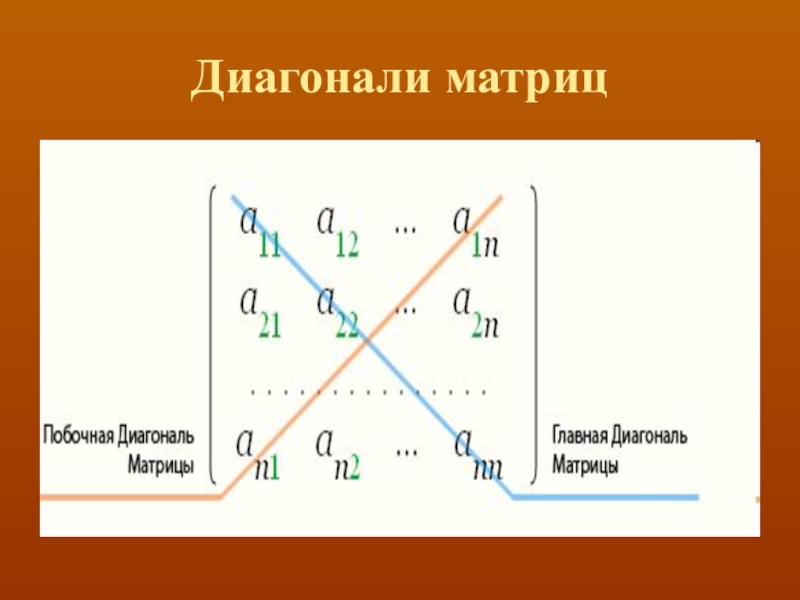
- 6. Диагонали матриц
- 7. Сложение матриц
- 8. Для обозначения произведения матрицы на число используется запись: С=А*λ= λ*А
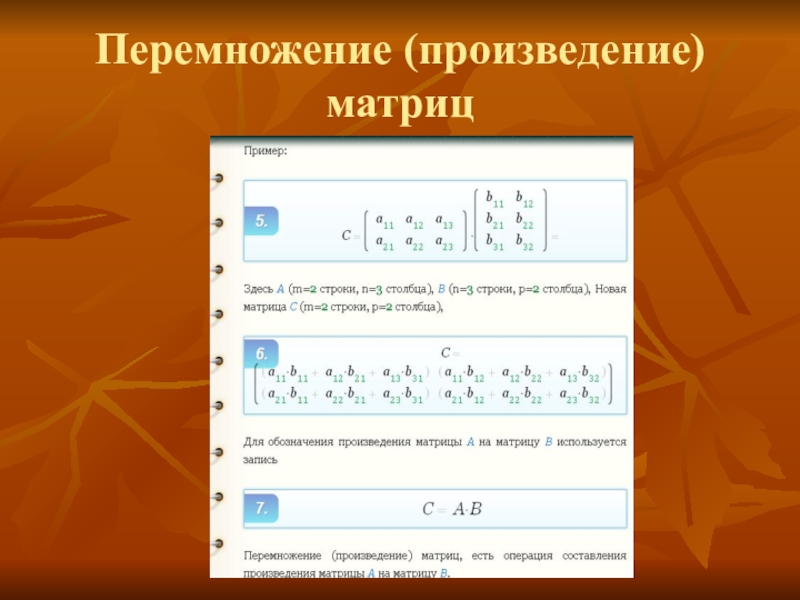
- 9. Перемножение (произведение) матриц
- 10. Условие перемножения (произведения) матрицМатрицу A можно умножить
- 11. Слайд 11
- 12. В математике рассматривается множество различных типов и
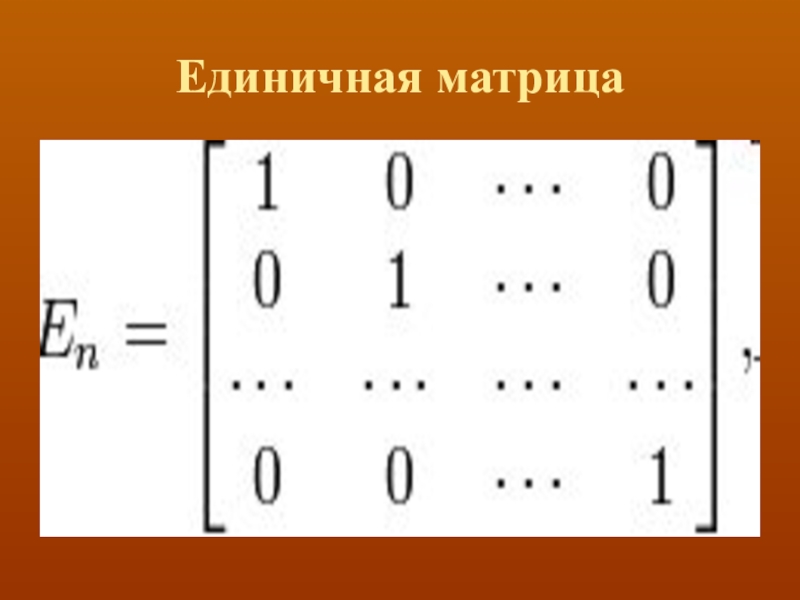
- 13. Единичная матрица
- 14. Единичные матрицы первых порядков имеют вид
- 15. Симметричная матрицаСимметричной (Симметрической) называют квадратную матрицу, элементы которой симметричны относительно главной диагонали.
- 16. Кососимметричная (кососимметрическая)матрица — квадратная матрица А над
- 17. Кососимметричная матрица
- 18. Верхнетреугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.
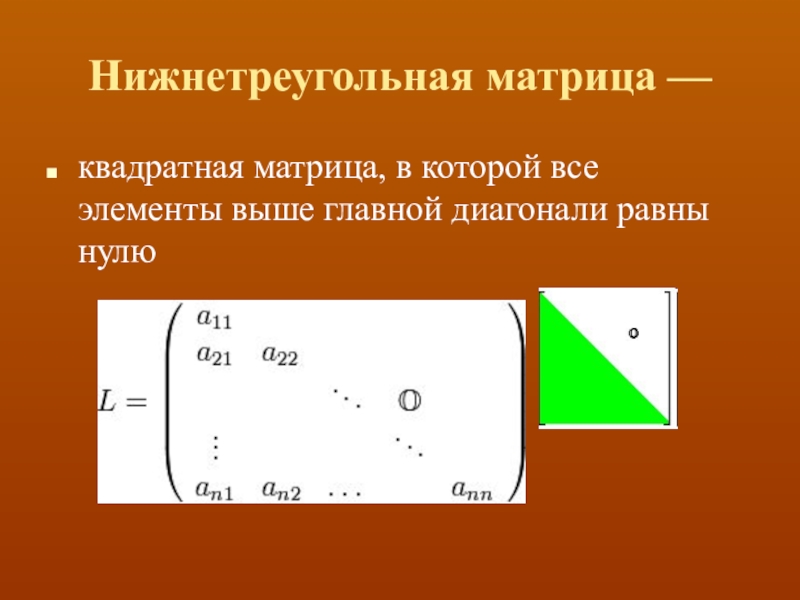
- 19. Нижнетреугольная матрица —квадратная матрица, в которой все элементы выше главной диагонали равны нулю
- 20. Определи́тель (или детермина́нт) —одно из основных понятий
- 21. Алгоритм вычисления определителя матрицы:Для матрицы первого порядка детерминантом является сам единственный элемент этой матрицы:
- 22. Для матрицы 2х2 детерминант определяется как
- 23. Для матрицы n порядка определитель задаётся рекурсивно:
- 24. Для вычисления определителейможно применить два алгоритма: рекурсивный и итеративный.
- 25. Возьмём произвольный минор М1j.Он является определителем матрицы
- 26. Число операций,Необходимых для рекурсивного вычисления определителя матрицы
- 27. Недостаток рекурсивного алгоритма:Количество операций при каждом вызове
- 28. Итеративный алгоритм:использует элементарные преобразования, приводящие матрицу к
- 29. Недостаток итеративного метода:Производится большое количество операций деления. Большие колебания значений элементов матрицы приводят к значительным погрешностям.
- 30. Реализация на Паскале рекурсивной функции вычисления определителей:Function
- 31. Реализация на Паскале итеративной функции вычисления определителей:Function
- 32. Реализация на Паскале итеративной функции вычисления определителей:
- 33. Домашнее задание:
- 34. Скачать презентанцию
Матрицы— это прямоугольные таблицы из чисел, содержащие m строк и n столбцов. Числа m и n называются порядками матрицы.
Слайды и текст этой презентации
Слайд 3Ма́трица
— математический объект, записываемый в виде прямоугольной таблицы элементов кольца
или поля (например, целых или комплексных чисел), которая представляет собой
совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.Слайд 4Матрицы допускают следующие алгебраические операции:
сложение матриц, имеющих один и тот
же размер;
умножение матриц подходящего размера (матрицу, имеющую n столбцов, можно
умножить справа на матрицу, имеющую n строк);умножение матрицы на элемент основного кольца или поля (т. н. скаляр).
Слайд 5Матрицы записываются с помощью больших круглых скобок
a11 a12
… a1n
a21 a22
… a2n . . . . . . . . . . . . . . .
am1 am2 … amn
Слайд 10Условие перемножения (произведения) матриц
Матрицу A можно умножить не на всякую
матрицу B. Необходимо, чтобы число столбцов матрицы A было равно
числу строк матрицы BОба произведения A·B и B·A можно определить только в том случае, когда число столбцов A совпадает с числом строк B, а число строк A совпадает с числом столбцов B. При этом обе матрицы A·B и B·A будут квадратными, но порядки их будут разными.
Чтобы оба произведения A·B и B·A были определены и имели одинаковый порядок, необходимо и достаточно, чтобы матрицы A и B были квадратными матрицами одного порядка.
Слайд 12
В математике рассматривается множество различных типов и видов матриц. Таковы,
например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.
Слайд 15Симметричная матрица
Симметричной (Симметрической) называют квадратную матрицу, элементы которой симметричны относительно
главной диагонали.
Слайд 16Кососимметричная (кососимметрическая)
матрица — квадратная матрица А над полем k характеристики,
отличной от 2, удовлетворяющая соотношению:
AT = − A,
где AT —
транспонированная матрица.Слайд 18Верхнетреугольная матрица —
квадратная матрица, в которой все элементы ниже
главной диагонали равны нулю.
Слайд 19Нижнетреугольная матрица —
квадратная матрица, в которой все элементы выше главной
диагонали равны нулю
Слайд 20Определи́тель (или детермина́нт) —
одно из основных понятий линейной алгебры. Определитель
матрицы является многочленом от элементов квадратной матрицы (то есть такой,
у которой количество строк и столбцов равно).Определитель матрицы А обозначается как: det(A), |А| или Δ(A).
Слайд 21Алгоритм вычисления определителя матрицы:
Для матрицы первого порядка детерминантом является сам
единственный элемент этой матрицы:
Слайд 23Для матрицы n порядка определитель задаётся рекурсивно:
где М1j— дополнительный
минор к элементу a1j.
Эта формула называется разложением по строке.
Слайд 25
Возьмём произвольный минор М1j.
Он является определителем матрицы порядка n-1. Для
его нахождения необходимо решить такую же задачу, только меньшей размерности.
Следовательно,
необходимо применить рекурсивный алгоритм. Слайд 26Число операций,
Необходимых для рекурсивного вычисления определителя матрицы порядка n, определяется
количеством рекурсивных вызовов, а также числом операций, совершаемых во время
одного вызова.Слайд 27Недостаток рекурсивного алгоритма:
Количество операций при каждом вызове пропорционально n2. Следовательно,
временная сложность алгоритма равна Q(n2n!), что делает малоэффективным для больших
значений n.Слайд 28Итеративный алгоритм:
использует элементарные преобразования, приводящие матрицу к треугольному виду. Определитель
такой матрицы равен произведению значений элементов, находящихся на главной диагонали.
Слайд 29Недостаток итеративного метода:
Производится большое количество операций деления. Большие колебания значений
элементов матрицы приводят к значительным погрешностям.
Слайд 30Реализация на Паскале рекурсивной функции вычисления определителей:
Function cdet(var x:mat; t:integer):real;
var
i, j, k : integer;
s :
real; minor : mat;
Begin
if t=1 then calcul:=x[1,1] {элементарный случай}
else begin
s:=0;
for k:=1 to t do begin
for i:=1 to t+1 do
for j:=1 to k-1 do minor[I,j]:=x[i+1,j];
for i:=1 to t+1 do
for j:=k to t+1 do minor [I,j]:=x[i+1, j+1];
if odd(k) then s:=s+x[1,k]*cdet(minor, t-1) {рекурсивный вызов}
else s:=s-x[1,k]*cdet(minor, t-1);
end;
cdet:=s;
end;
end.;
Слайд 31Реализация на Паскале итеративной функции вычисления определителей:
Function CID(x:mat; r:integer): real;
var i, j, k : integer;
q
: real;Begin {CID}
for i:=1 to r-1 do begin
if x[I,i]:=0 then
begin
k:=1;
for j:=i+1 to r do
if x[j,i]<>0 then k:=j;
if k=1 then begin CID:=0; exit; end
else
for j:=1 to r do
begin
q:=x[i,j];
x[i,j]:=x[k,j];
x[k,j]:=-q;
end;
end;
Слайд 32Реализация на Паскале итеративной функции вычисления определителей:
{преобразование строк
с целью обнуления элементов в столбце i, расположенных под диагональю}
for j:=i+1 to x do
begin
q:=-x[j,i]/x[I,i];
for k:=1 to r do x[j,k]:=x[j,k]+x[I,k]*q;
end;
end;
{вычисление значения определителя треугольной матрицы}
q:=1;
for i:=1 to r do q:=q*x[I,i];
CID:=q;
End;