Слайд 1Решение текстовых
логических
задач
Слайд 2Ответьте на вопросы
да –
нет -
3. Определить истинно ли выражение:
1) «наличие аттестата
о среднем образовании достаточно для поступления в институт»
2) «наличие аттестата о среднем образовании необходимо для поступления в институт»
1. Являются ли следующие предложения логическими высказываниями:
1) сегодня отличная погода;
2) 2 + 3 = 4;
2. Являются ли высказывания отрицаниями друг друга:
1) «существуют белые слоны» и «все слоны серые»
2) «10 > 9» и «10 ≤ 9»
Слайд 4Способы решения задач:
С использованием средств алгебры логики
Табличный
C помощью рассуждений
переход на
последний
слайд
Слайд 5Решение задач средствами алгебры логики.
Изучается условие задачи.
Вводится система обозначений для
логических высказываний.
Конструируется логическая формула, описывающая логические связи между всеми высказываниями
условия задачи.
Определяются значения истинности этой логической формулы.
Из полученных значений истинности формулы определяются значения истинности логических высказываний.
Слайд 6Задача 1. История с амфорой
Алеша, Боря и Гриша нашли
а земле сосуд. Рассматривая удивительную находку, каждый высказал по два
предположения:
Алеша: «Это сосуд греческий и изготовлен в V веке.»
Боря: «Это сосуд финикийский и изготовлен он в III веке.»
Гриша: «Это сосуд не греческий и изготовлен в IV веке.»
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предположений. Где и в каком веке изготовлен сосуд?
Слайд 7Ввод системы обозначений
Сосуд греческий – Г
Сосуд финикийский – Ф
Сосуд изготовлен
в III веке – В3
Сосуд изготовлен в IV веке В4
Сосуд
изготовлен в V веке В5
Слайд 8Формализация задачи
Из слов учителя следует, что Алеша прав только в
чем-то одном: или Г=1 или В5=1. Тождественно истинным будет высказывание
Из слов Бори и учителя следует:
Из слов Гриши и учителя следует:
Слайд 9Конструирование логической формулы
Логическое произведение данных истинных высказываний должно быть тождественно
истинным
Слайд 10Определение истинности формулы
Упростим высказывание
Сосуд не может быть одновременно греческим и
не греческим, значит это выражение равно 0
Сосуд не может быть
одновременно греческим и финикийским, значит это выражение равно 0
Сосуд не может быть одновременно греческим и не греческим, значит это выражение равно 0
Сосуд не может быть одновременно изготовлен в 4 и 3 веках, значит это выражение равно 0
Сосуд не может быть одновременно греческим и финикийским, значит это выражение равно 0
Сосуд не может быть одновременно изготовлен в 5 и 3 веках, значит это выражение равно 0
Сосуд не может быть одновременно греческим и не греческим, значит это выражение равно 0
Слайд 11Определение значений истинности логических высказываний
Высказывание
истинно только при
, ,
,
, .
Таким образом, сосуд финикийский и изготовлен в V веке.
Задача решена.
Вернуться к оглавлению
Слайд 12Дорожное происшествие
Виновник ночного дорожно-транспортного происшествия скрылся с места аварии. Первый
из опрошенных свидетелей сказал работникам ГИБДД, что это были «Жигули»,
первая цифра номера машины – единица. Второй свидетель сказал, что машина была марки «Москвич», а номер начинался с семерки. Третий свидетель заявил, что машина была иностранная, номер начинался не с единицы. При дальнейшем расследовании выяснилось, что каждый из свидетелей правильно указал либо только марку машины, либо только первую цифру номера.
Какой марки была машина и с какой цифры начинался номер?
Слайд 13Ответ
Марка машины – «Жигули», номер начинается с семерки
Слайд 14Табличный способ решения задач
При использовании этого способа условия,
которые содержит задача, и результаты рассуждений фиксируются с помощью специально
составленных таблиц
Слайд 15Задача 1 Симфонический оркестр
В симфонический оркестр приняли на работу трех
музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте,
альте, кларнете, гобое
и трубе. Известно, что:
1) Смит – самый высокий;
2) играющий на скрипке меньше ростом играющего на флейте;
3) играющие на скрипке и флейте и Браун любят пиццу;
4) когда между альтистом и трубачом возникает ссора, Смит мирит их
5) Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?
Слайд 16 Так как музыкантов трое, инструментов шесть и каждый
владеет только двумя инструментами, получается, что каждый музыкант играет на
инструментах, которыми остальные не владеют.
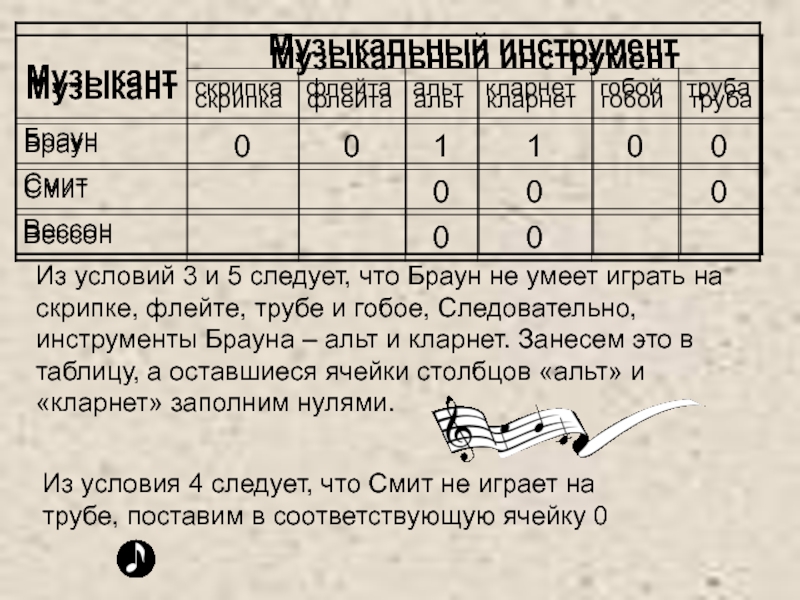
Составим таблицу и отразим в ней
условия задачи, заполнив соответствующие клетки 0 и 1 в зависимости от того, ложно или истинно соответствующее высказывание.
Слайд 17Из условий 3 и 5 следует, что Браун не умеет
играть на скрипке, флейте, трубе и гобое, Следовательно, инструменты Брауна
– альт и кларнет. Занесем это в таблицу, а оставшиеся ячейки столбцов «альт» и «кларнет» заполним нулями.
Из условия 4 следует, что Смит не играет на трубе, поставим в соответствующую ячейку 0
Слайд 18
Из таблицы видно, что на трубе играть может только Вессон.
В соответствующую ячейку поставим 1. Из условий 1 и 2
, следует, что Смит не скрипач. Заполняем соответствующую ячейку 0
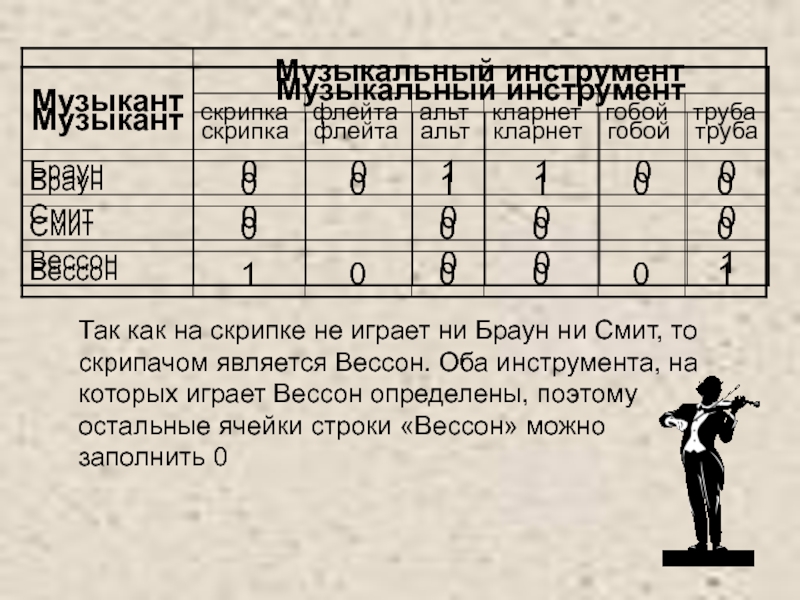
Слайд 19Так как на скрипке не играет ни Браун ни Смит,
то скрипачом является Вессон. Оба инструмента, на которых играет Вессон
определены, поэтому остальные ячейки строки «Вессон» можно заполнить 0
Слайд 20
Из таблицы видно, что на флейте и гобое играть может
только Браун
Задача решена:
Браун играет на альте и кларнете,
Смит
– на флейте и гобое,
Вессон на скрипке и трубе
Вернуться к оглавлению
Слайд 21Задача 2. Спортсмены.
На зимние соревнования приехали Джессика, Ник
и Линда из городов Лас-Вегаса, Монреаля, Денвера. Ребята занимаются разными
видами спорта: фигурным катанием, хоккеем, горнолыжным спортом.
Известно, что:
1) Джессика не любит хоккей, но хотела бы съездить и посмотреть Монреаль и Денвер;
2) Ник хотел бы поехать в Денвер;
3) Линда плохо катается на коньках.
Кто в каком городе живет каким видом спорта занимается?
Слайд 22Ответ
Джессика живет в Лас-Вегасе и занимается фигурным
катанием
Ник живет в Монреале и занимается хоккеем
Линда из Денвера, катается на горных лыжах
Слайд 23Решение задач с помощью рассуждений
Данные метод решения называют еще методом
перебора. Выдвигается некая гипотеза, которая подтверждается или опровергается в ходе
дальнейших рассуждений. Гипотезы выдвигаются до тех пор, пока не найдется единственный вариант. Если при рассмотрении какой-то гипотезы получен ответ на вопрос задачи, надо обязательно проверить и другие варианты для подтверждения того, что найденное решение является единственным.
Слайд 24Задача 1. Фамилии попутчиков.
В поездке пятеро друзей –
Антон, Борис, Вадим, Дима и Гриша познакомились с попутчицей. Они
предложили ей отгадать их фамилии, причем каждый из них высказал одно истинное и одно ложное утверждение.
Дима: «Моя фамилия – Мишин, а фамилия Бориса – Хохлов»
Антон: «Мишин – это моя фамилия, а фамилия Вадима – Белкин»
Борис: «Фамилия Вадима – Тихонов, а моя фамилия – Мишин»
Вадим: «Моя фамилия – Белкин, а фамилия Гриши – Чехов»
Гриша: «Да, моя фамилия – Чехов, а фамилия
Антона – Тихонов.
Какую фамилию носит каждый из друзей?
Слайд 25Допустим сначала, что фамилия Димы – Мишин. Но если это
утверждение истинно, то у Антона и у Бориса должны быть
другие фамилии, значит утверждения Антон - Мишин и
Борис - Мишин ложны.
В этом случае должны быть истинны утверждения Вадим - Белкин и
Вадим - Тихонов, но Вадим не может одновременно носить две фамилии.
Получили противоречие. Значит предположение, что фамилия Димы – Гришин, неверно
Слайд 26Допустим, что фамилия Бориса – Хохлов.
Этот случай приводит к цепочке
умозаключений:
утверждение Борис Хохлов истинно
утверждение Борис Мишин ложно
утверждение Вадим
Тихонов истинно
утверждение Антон Тихонов ложно
утверждение Гриша Чехов истинно
утверждение Вадим Белкин ложно
утверждение Антон Мишин истинно.
Из данной цепочки можно сделать вывод, что фамилия Димы – Белкин.
Слайд 27Задача решена:
Борис – Хохлов
Вадим – Тихонов
Гриша – Чехов
Антон – Мишин
Дима
- Белкин
Слайд 28Задача 2. Иностранные языки.
Вадим, Сергей и Михаил
изучают разные иностранные языки: китайский, японский и арабский. На вопрос,
какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский».
Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два остальных ложны.
Какой язык изучает каждый
из молодых людей?
Слайд 29Ответ
Сергей изучает китайский язык
Михаил изучает японский язык
Вадим изучает арабский язык.
Слайд 30Выводы
Способ решения текстовых логических задач выбирается в зависимости
от условия задачи
Универсальным способом решения задач является способ
рассуждений
Слайд 31Домашнее задание
Шорти Финелли был найден убитым, полиция арестовала
по подозрению в убийстве троих: Бака, Джо и Тилпи. На
допросе задержанные дали следующие показания.
Бак: «Я не убивал. Я никогда не видел Джо раньше. Я знаю Шорти».
Джо: «Я не убивал. Бак и Тилпи – мои приятели. Бак никогда никого не убивал».
Тилпи: «Я не убивал. Бак лжет, говоря, что он никогда раньше не видел Джо. Я знаю, кто из двух других подозреваемых – убийца».
Известно, что одно из высказываний каждого из задержанных ложно и один из подозреваемых – убийца. Кто убийца?