Слайд 1Мастер-класс
«Применение теории графов к решению задач»
Слайд 2«Чтоб мудро жизнь прожить
Знать надобно немало…»
О.Хайям
Цель:
сформировать представления о сферах применения графов, о способах решения
задач с помощью графов; закрепить умение строить графы (деревья).
Задачи:
Создать мотивационную базу для изучения материала.
показать красоту этого метода.
выбирать наиболее эффективные решения поставленной задачи.
Слайд 3Планируемые учебные результаты:
Предметные: развитие представления о графах как вспомогательных средствах
при решении задач;
Метапредметные: формирование умения выделять существенные признаки объекта и
отношения между объектами; ИКТ-компетентность (умение строить схемы);
Личностные: формирование способности увязать учебное содержание с собственным жизненным опытом, понять значение информационного моделирования как метода познания окружающей действительности.
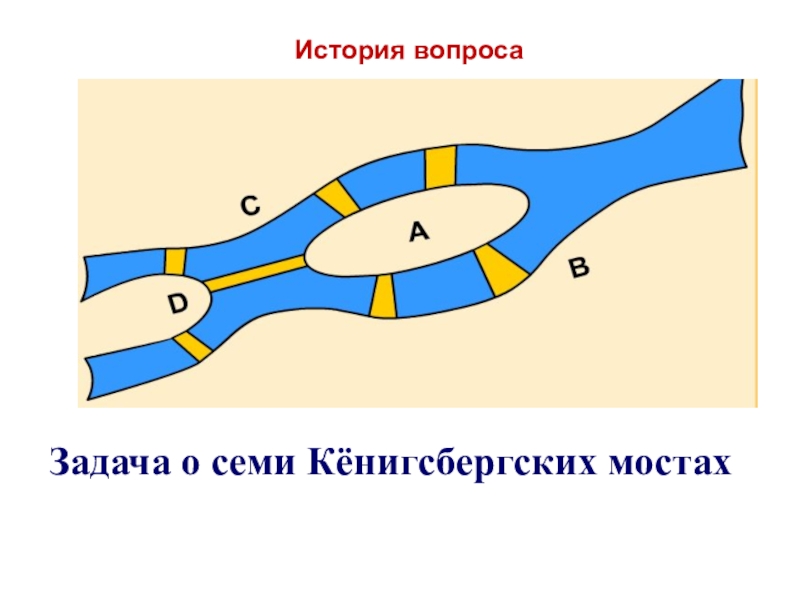
Слайд 4История вопроса
Задача о семи Кёнигсбергских мостах
Слайд 5Основные понятия
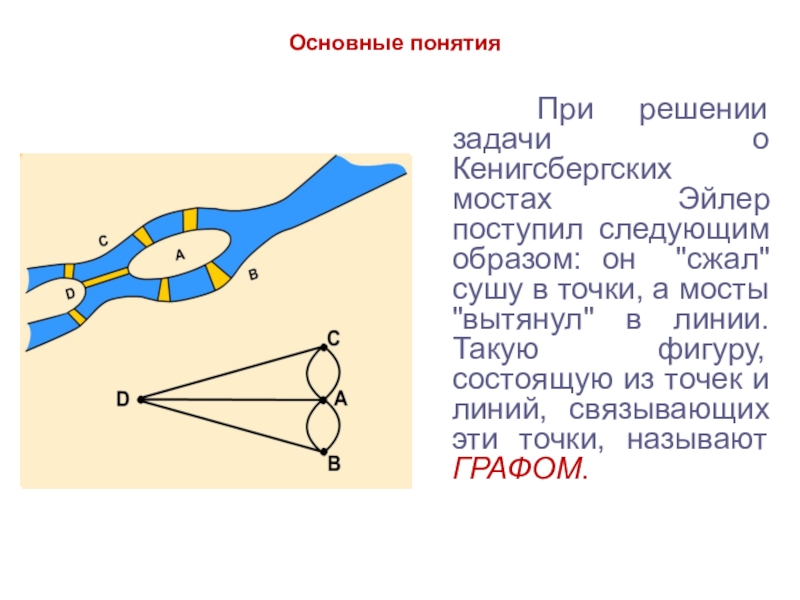
При решении задачи о Кенигсбергских мостах Эйлер
поступил следующим образом: он "сжал" сушу в точки, а мосты
"вытянул" в линии. Такую фигуру, состоящую из точек и линий, связывающих эти точки, называют ГРАФОМ.
Слайд 6 Точки А, В, С, D называют ВЕРШИНАМИ графа, а
линии, которые соединяют вершины, - РЕБРАМИ графа.
Вершины, из которых
выходит нечетное число ребер, называются НЕЧЕТНЫМИ вершинами,
а вершины, из которых выходит четное число ребер, называются ЧЕТНЫМИ.
Слайд 7Свойства графов
Решая задачу про Кенигсбергские мосты, Эйлер установил, в частности,
следующие СВОЙСТВА графа:
Если в фигуре только четные вершины ,
то ее можно нарисовать одним росчерком, независимо от того, с какого места начинается черчение.
2) Если в фигуре имеется только одна пара нечетных вершин, то такую фигуру можно нарисовать одним росчерком, начав черчение в одной из нечетных вершин.
3) Если фигура имеет более одной пары нечетных вершин, то она вовсе не может быть нарисована одним росчерком.
В задаче о семи Кенигсбергских мостах все четыре вершины соответствующего графа - нечетные, т.е. нельзя пройти по всем мостам ровно один раз и закончить путь там, где он был начат.
Слайд 8Свойства графов
Кроме трех свойств графа, которые установил Эйлер, решая задачу
про Кенигсбергские мосты, он вывел еще два СВОЙСТВА:
4)
Число нечетных вершин графа всегда четно.
5) Если в графе имеются нечетные вершины, то наименьшее число росчерков, которыми можно нарисовать граф, равно половине числа нечетных вершин этого графа.
Например, если фигура имеет четыре нечетные вершины, то ее можно начертить самое меньшее двумя росчерками.
Слайд 9Этот вопрос положил начало циклу новых увлекательных задач:
если дана
геометрическая фигура, как начертить ее на бумаге одним росчерком пера,
не проводя дважды ни одну линию?
Например: как проложить дорожки в дендропарке, чтобы посетители увидели все растения не проходя дважды по одной.
Слайд 10
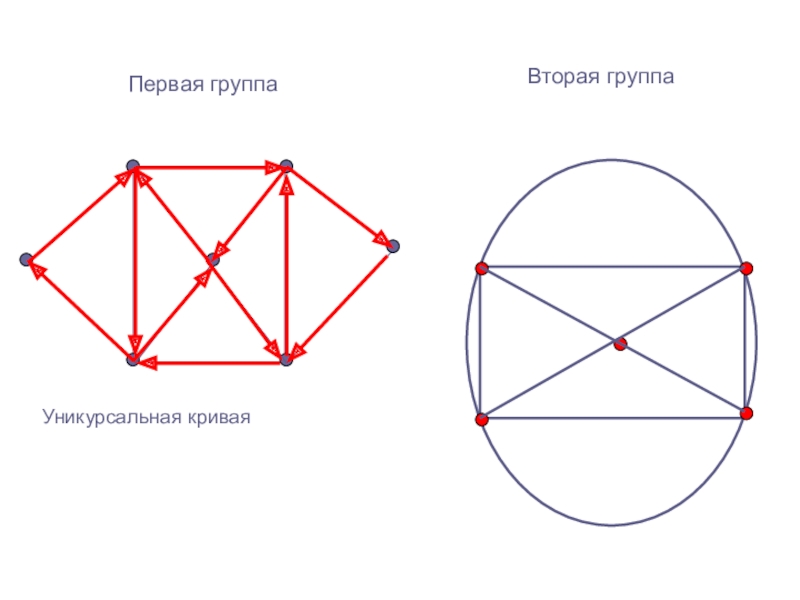
Первая группа
Вторая группа
Уникурсальная кривая
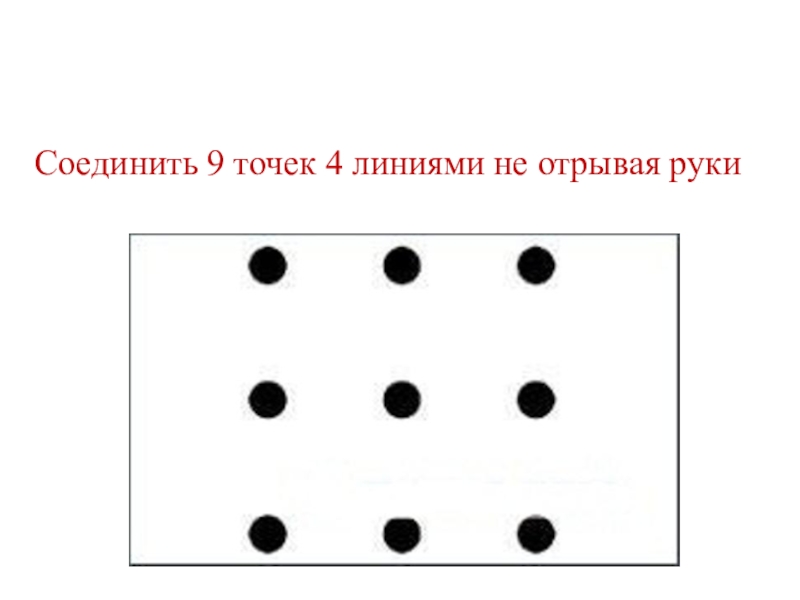
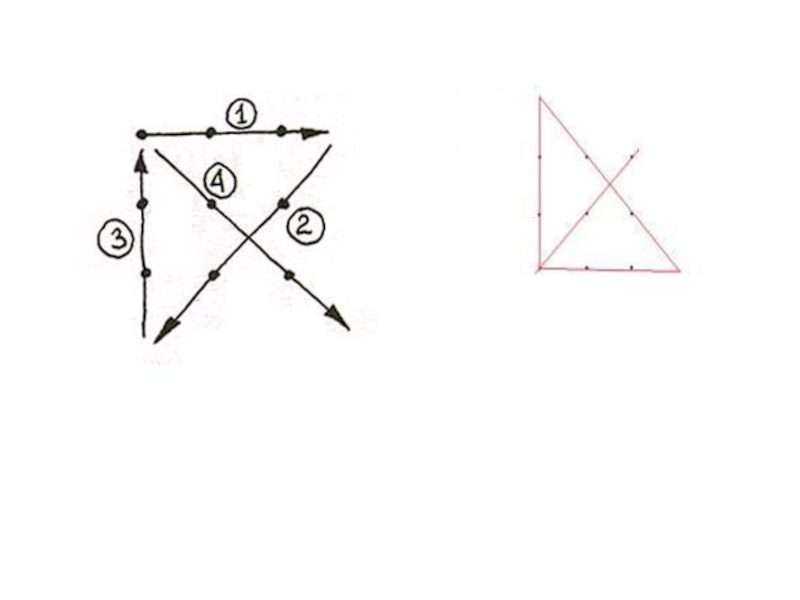
Слайд 11 Соединить 9 точек 4 линиями не отрывая руки
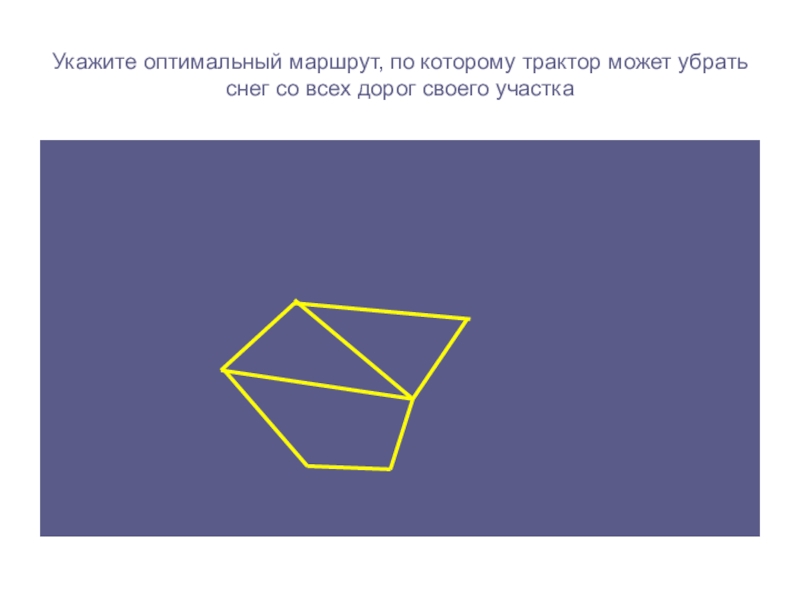
Слайд 13Укажите оптимальный маршрут, по которому трактор может убрать снег со
всех дорог своего участка
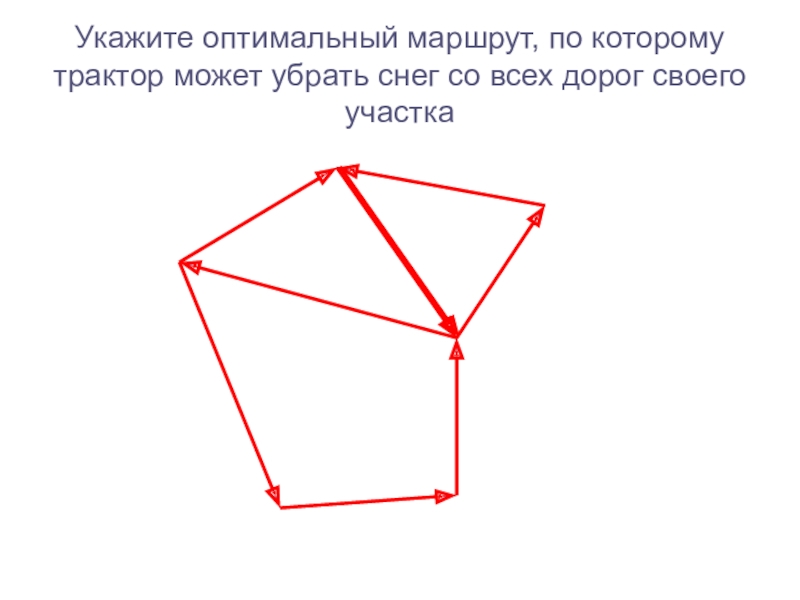
Слайд 14Укажите оптимальный маршрут, по которому трактор может убрать снег со
всех дорог своего участка
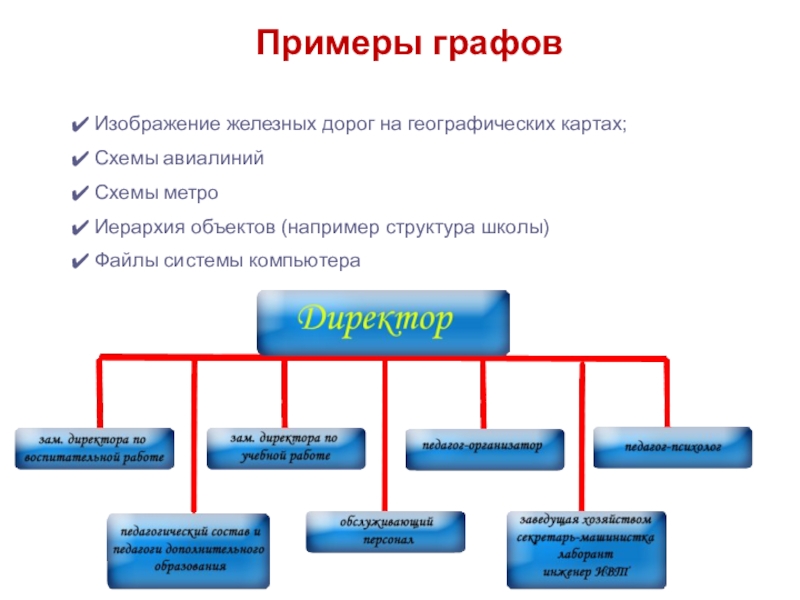
Слайд 15Примеры графов
Изображение железных дорог на географических картах;
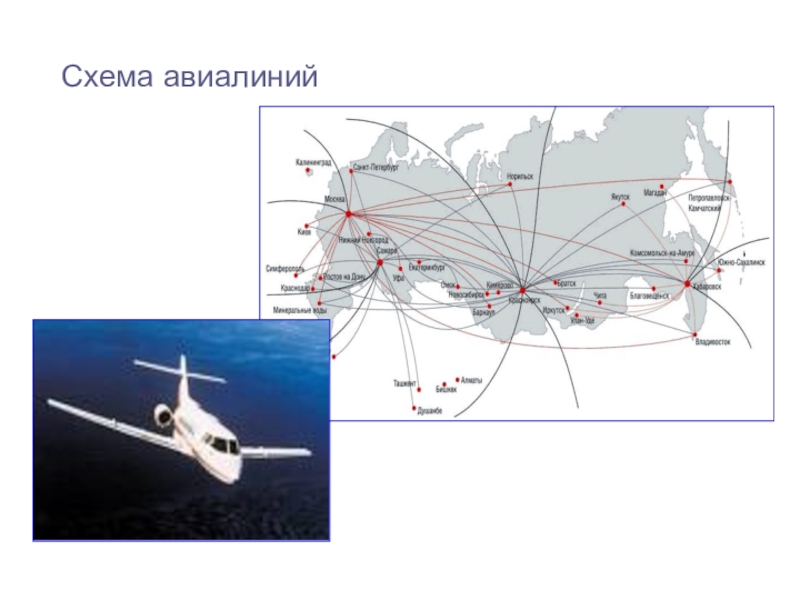
Схемы
авиалиний
Схемы метро
Иерархия объектов (например структура школы)
Файлы системы компьютера
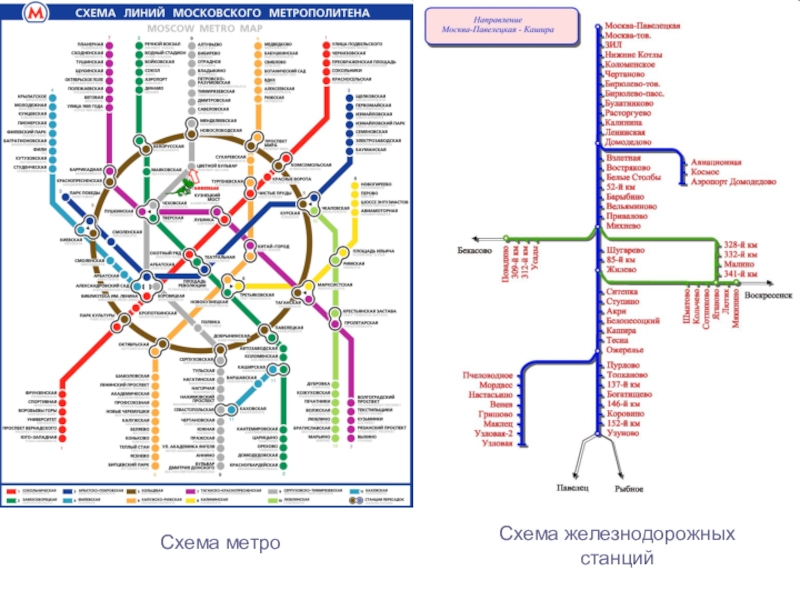
Слайд 16Схема метро
Схема железнодорожных станций
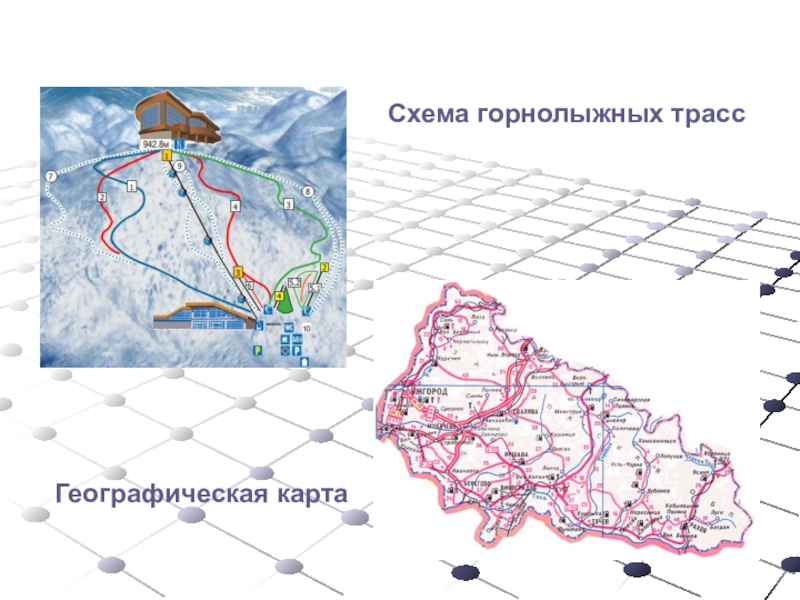
Слайд 17Схема горнолыжных трасс
Географическая карта
Слайд 20Теория графов находит применение, например, в геоинформационных системах (ГИС). Существующие
или вновь проектируемые дома, сооружения, кварталы и т. п. рассматриваются
как вершины, а соединяющие их дороги, инженерные сети, линии электропередачи и т. п. — как рёбра. Применение различных вычислений, производимых на таком графе, позволяет, например, найти кратчайший объездной путь или ближайший продуктовый магазин, спланировать оптимальный маршрут.
Слайд 21Графы используются:
В строительстве
для составления чертежей;
для расчета материала;
для расчета количества
рабочих;
для расчетов устойчивости откоса
В физике
Анализ электрических цепей распознаётся методом графов,
также применяется в классической электродинамике СТО, энергетике, радиоэлектронике и др.
В химии
Используется для составления формул
Для исследования стационарной кинетически ферментативных реакций
Слайд 22Финансы и кредит
«Теория графов в управлении организационными системами»
Экология
(геоботаника)
Метод графов при составлении дихотомических ключей для определения
растений.
Транспорт
Для расчета пассажиропотока
Медицина
Исследование биоритмов
Биология
Для анализа биологических структур и генных систем
Спорт
Разработка стратегии игры
Слайд 24С помощью построения графа решается ряд задач входящих в ЕГЭ
и ОГЭ:
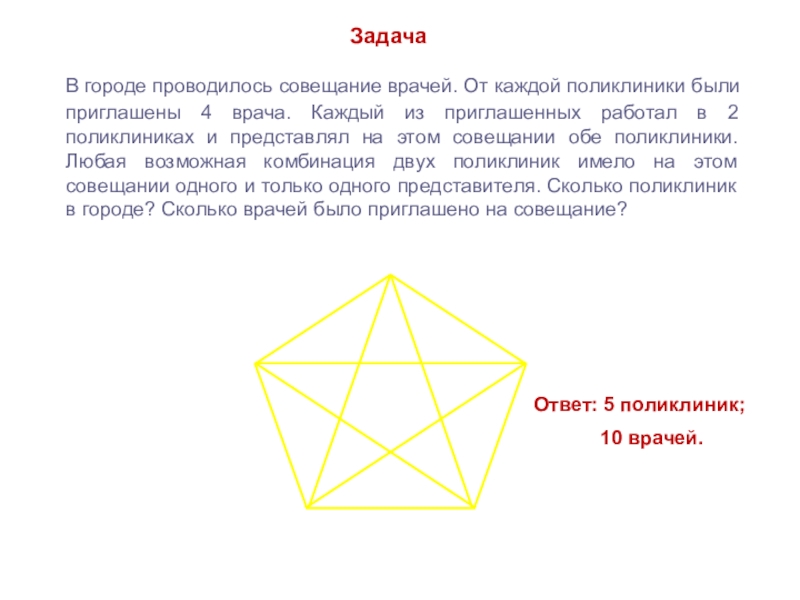
Слайд 25 В городе проводилось совещание врачей. От каждой поликлиники
были приглашены 4 врача. Каждый из приглашенных работал в 2
поликлиниках и представлял на этом совещании обе поликлиники. Любая возможная комбинация двух поликлиник имело на этом совещании одного и только одного представителя. Сколько поликлиник в городе? Сколько врачей было приглашено на совещание?
Задача
Ответ: 5 поликлиник;
10 врачей.
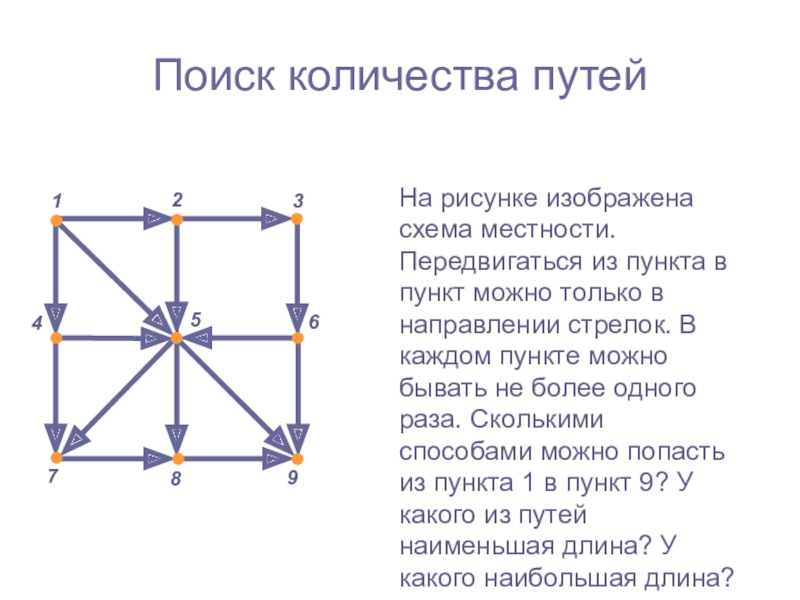
Слайд 26Поиск количества путей
На рисунке изображена схема местности. Передвигаться из пункта
в пункт можно только в направлении стрелок. В каждом пункте
можно бывать не более одного раза. Сколькими способами можно попасть из пункта 1 в пункт 9? У какого из путей наименьшая длина? У какого наибольшая длина?
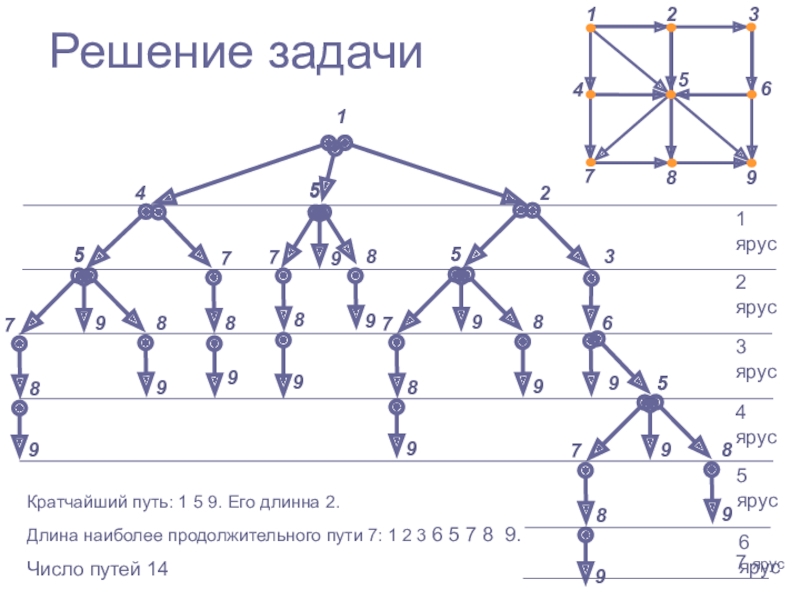
Слайд 27Решение задачи
Кратчайший путь: 1 5 9. Его длинна 2.
Длина наиболее
продолжительного пути 7: 1 2 3 6 5 7 8
9.
Число путей 14
Слайд 28Проблема трех домов и трех колодцев
Три соседа имеют три общих колодца.
Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу? Дорожки не могут
проходить через колодцы и домики.
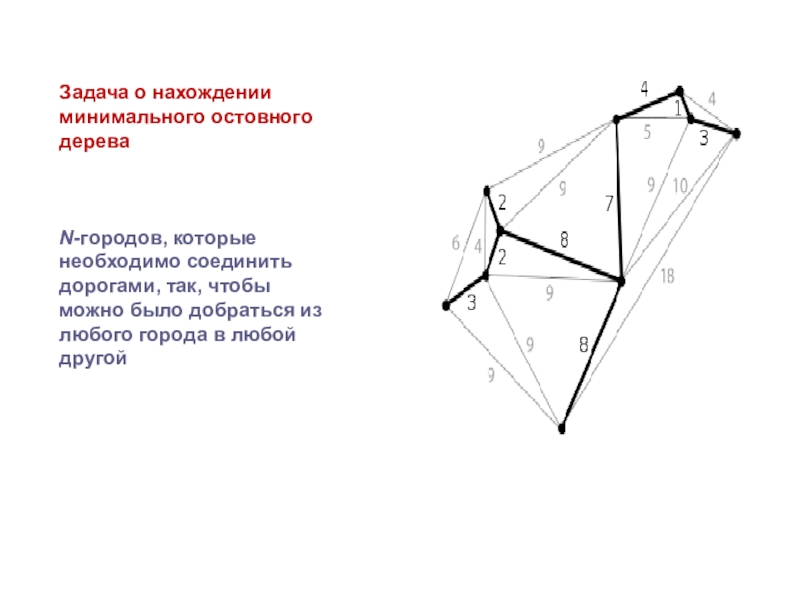
Слайд 30Задача о нахождении минимального остовного дерева
N-городов, которые необходимо соединить дорогами,
так, чтобы можно было добраться из любого города в любой
другой
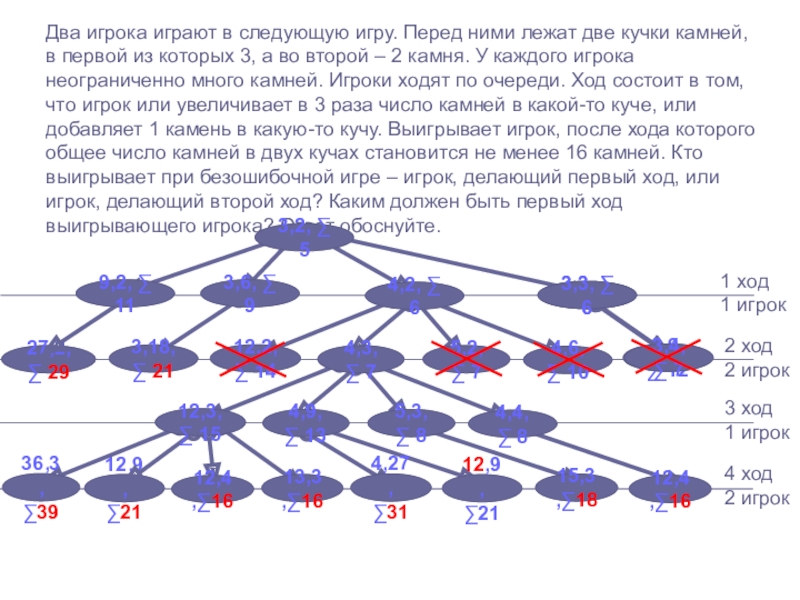
Слайд 31Два игрока играют в следующую игру. Перед ними лежат две
кучки камней, в первой из которых 3, а во второй
– 2 камня. У каждого игрока неограниченно много камней. Игроки ходят по очереди. Ход состоит в том, что игрок или увеличивает в 3 раза число камней в какой-то куче, или добавляет 1 камень в какую-то кучу. Выигрывает игрок, после хода которого общее число камней в двух кучах становится не менее 16 камней. Кто выигрывает при безошибочной игре – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.
3,18, ∑ 21
3,2, ∑ 5
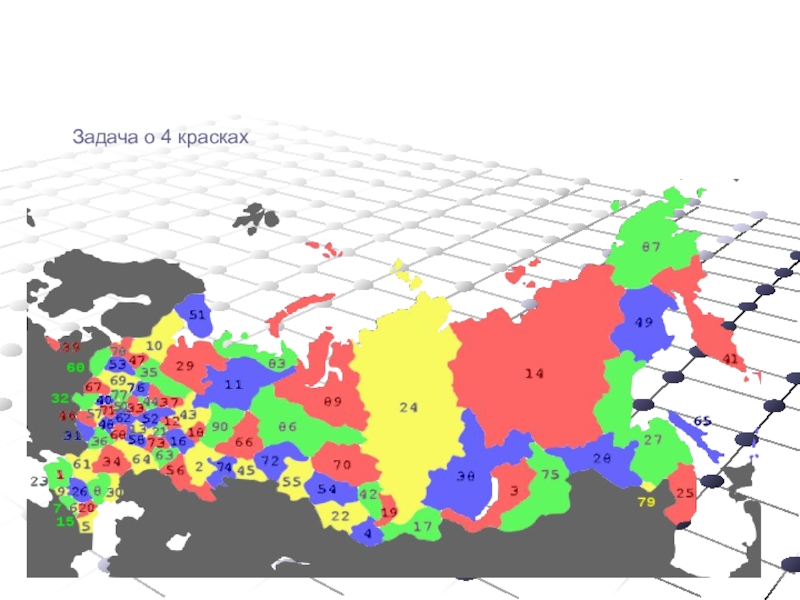
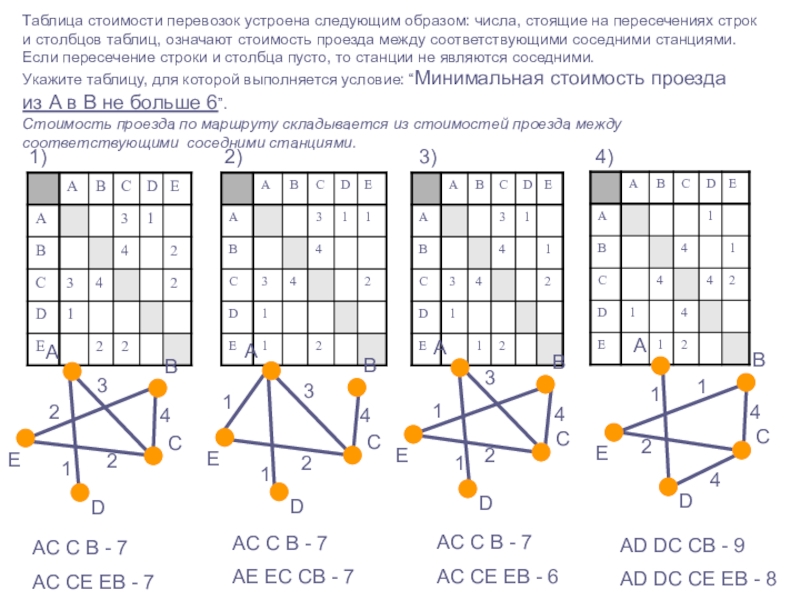
Слайд 32Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях
строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними
станциями. Если пересечение строки и столбца пусто, то станции не являются соседними.
Укажите таблицу, для которой выполняется условие: “Минимальная стоимость проезда
из А в B не больше 6”.
Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.
1)
2)
3)
4)
AC C B - 7
AC CE EB - 7
AC C B - 7
AE EC CB - 7
AC C B - 7
AC CE EB - 6
AD DC CB - 9
AD DC CE EB - 8
Слайд 33Рефлексия
Выберите ответ:
1. На занятии я узнал что-то новое да
нет
2. На занятии мне понравилось:
история графов
практические задания
3. Я применю это в своей практике да нет