Слайд 1МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА
ДЛЯ 10 КЛАССА
«СОРТИРОВКА МАССИВОВ
В СРЕДЕ
DELPHI-LAZARUS»
ШУНТОВА ЛЮДМИЛА ВЛАДИМИРОВНА
учитель информатики
МБОУ Лесногородской сош
Одинцовского
района Московской области
2013 год
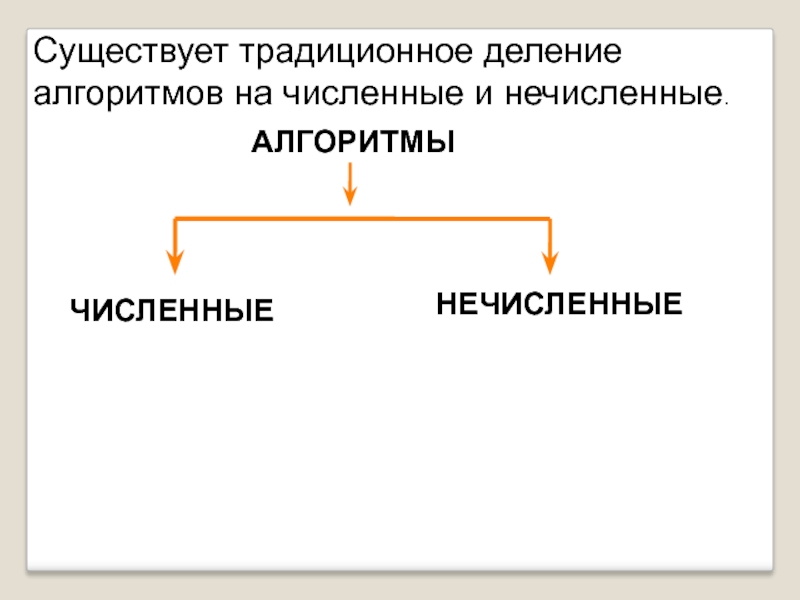
Слайд 2Существует традиционное деление алгоритмов на численные и нечисленные.
АЛГОРИТМЫ
ЧИСЛЕННЫЕ
НЕЧИСЛЕННЫЕ
Слайд 3ЧИСЛЕННЫЕ АЛГОРИТМЫ
Математические расчеты
(вычисления по формулам,
решение уравнений,
статистическая обработка и т.д.
ДАННЫЕ -ЧИСЛА
Слайд 4АЛГОРИТМЫ
НЕЧИСЛЕННЫЕ АЛГОРИТМЫ
Системное программирование
(трансляторы, ОС),СС
управления Б.Д.,
сетевое программное обеспечение и т.д.
ДАННЫЕ-символьная,графическая, мультимедийная информация
Слайд 5Для программных продуктов второй категории наиболее часто используемыми являются алгоритмы
сортировки данных.
От эффективности их выполнения во многом зависит эффективность работы
всей программы.
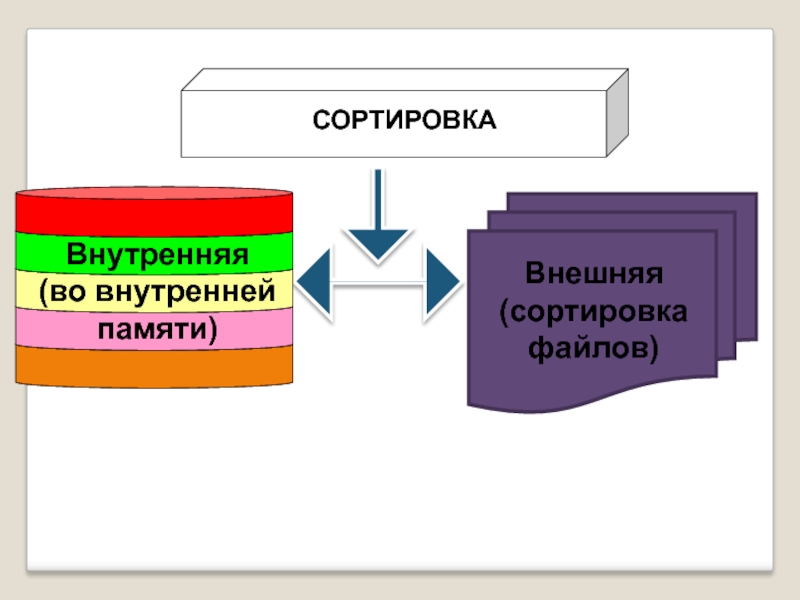
Различают алгоритмы
внутренней сортировки – во внутренней памяти внешней сортировки- сортировки файлов
Слайд 6
Внешняя
(сортировка файлов)
Внутренняя
(во внутренней памяти)
СОРТИРОВКА
Слайд 7Речь пойдет только о внутренней сортировке
Как правило, сортируемые данные располагаются
в массивах.
В простейшем случае – сортируются числовые массивы.
Слайд 8Сортировка- упорядочивание данных по некоторому признаку.
(И.Г.Семакин)
Сортировка-процесс размещения заданного множества объектов
в определенном порядке (убывания или возрастания)
(Д.Златопольский)
Сортировка- один из наиболее распространенных
процессов современной обработки информации. Это распределение элементов множества по группам в соответствии с определенными правилами.
(Е.В.Андреева)
Слайд 9
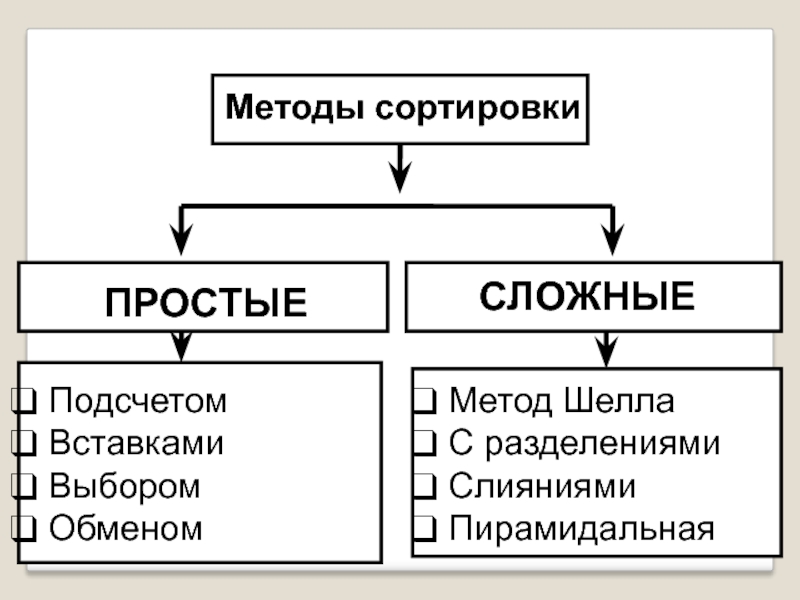
Методы сортировки
ПРОСТЫЕ
СЛОЖНЫЕ
Подсчетом
Вставками
Выбором
Обменом
Метод Шелла
С разделениями
Слияниями
Пирамидальная
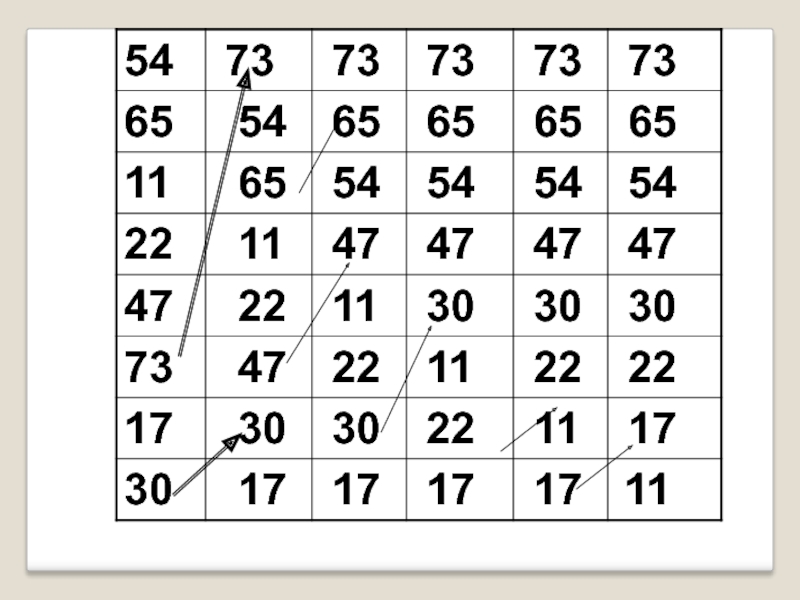
Слайд 10СОРТИРОВКА ПОДСЧЕТОМ
Место каждого элемента в отсортированном массиве зависит от количества
элементов, меньших его.
Например, если значение некоторого элемента исходного массива
превышает значения четырех других, то его место в упорядоченной последовательности- пятое.
Следовательно, для сортировки надо для каждого элемента массива подсчитать к-во эл-тов, меньших его, и затем разместить каждый рассмотренный элемент на соответствующем месте в новом, специально созданном , массиве.
Слайд 11
Исходный массив
12
32
5
6
19
20
3
10
3
5
6
10
12
19
20
32
Упорядоченный массив
1 место
(0 элем)
2 место
(1 элем)
3 место
(2 элем)
4 место
(3
элем)
5 место
(4 элем)
6 место
(5 элем)
7 место
(6 элем)
8 место
(7 элем)
Слайд 12алг.Сортировка подсчетом
{подсчитываем значение k [i] для каждого элемента массива
Слайд 13СОРТИРОВКА ВЫБОРОМ
Сначала в неупорядоченном массиве выбирается минимальный элемент.
Этот
элемент исключается из дальнейшей обработки , а оставшаяся последовательность элементов
принимается за исходную, и процесс повторяется до тех пор, пока все элементы не будут выбраны. Выбранный в исходном массиве минимальный элемент размещается на первом месте в новом массиве.
Однако если на втором просмотре исходного массива вновь найти минимальный элемент, то им окажется тот же самый элемент.
Чтобы исключить эту ситуацию, в исходном массиве вместо выбранного, записать число, заведомо превосходя-щее любой элемент исх.массива
Слайд 14алг.Сортировка выбором
{Находим минимальный элемент массива и его индекс}
min:=a[1] indmin:= 1
нц для j от 2
до n
если a [j] < a [indmin]
то {увеличиваем значение к для j-го элемента}
min:= a [j]
indmin := j
все
кц
{записываем минимальный элемент на i-е место в массиве b }
b [i] := min
{заменяем минимальный элемент исходного массива «большим числом»
b [i] := max
Кц
{выводим на экран отсортированный массив b}
нц для I от 1 до n
вывод b [i]
кц
кон
Слайд 15Второй способ сортировки выбором
Рассмотренный вариант сортировки обладает двумя недостатками:
Требование дополнительного
массива
Для нахождения минимального элемента и его индек-са на каждом проходе
приходится просматривать все элементы массива
Указанные недостатки устраняются, если все изменения проводить в исходном массиве:
Найти минимальный элемент среди всех элементов массива и поменять его местами с первым элементом
Найти минимальный элемент среди второго, третьего и т.д. элементов массива и поменять его местами со вторым элементом и т.д.
….
В данной разработке урока применяется именно этот способ
Слайд 16алг.Сортировка выбором
for i := 1 to Dreal - 1
do {i - позиция, в которую нужно записать}
begin Min1 :=
999999; {нач. значение для поиска минимальный элемента }
for j := i to Dreal do {Поиск минимального элемента }
begin if Mass [j] < Min1 then {в оставшейся части массива }
begin k := j; Min1 := Mass [j]; {к - номер найденного элемента }
end; {Min1 - найденное значение }
end; { }
rab := Mass[i]; {Обмен элементов массива }
Mass [i] := Min1; {с номерами (i) и (k) }
Mass [k] := rab; { }
sss := ''; {Вывод }
for rab := 1 to dreal do {текущего }
begin sss := sss + intToStr(Mass[rab]) + ' '; {состояния }
end; {массива }
ListBox3.Items.Add(sss); {в список }
ListBox3.ItemIndex := ListBox3.Count - 1; {ListBox3 }
sleep(5000); {Задержка }
end;
ListBox3.Items.Add('OK !'); {Вывод "OK"}
end;
Слайд 17СОРТИРОВКА ОБМЕНОМ
Метод «пузырька»
Метод, при котором все соседние элементы массива попарно
сравниваются друг с другом и меняются местами, если предшествующий элемент
больше последующего.
В результате максимальный элемент постепенно смещается вправо и в конце концов занимает свое место (которое он должен занимать в упорядоченном массиве –крайнее правое), после чего этот элемент исключается из дальнейшей обработки.
Затем процесс повторяется , и свое место занимает второй по величине элемент. Так продолжается до тех пор, пока весь массив не будет упорядочен.
Слайд 18
Если последовательность сортируемых чисел расположить вертикально (где первый элемент исходного
массива –внизу)
и проследить за перемещением элементов, то можно увидеть,
что большие элементы ,
подобно пузырькам воздуха в воде, «всплывают» на соответствующую позицию.
Поэтому по аналогии эту сортировку называют «методом пузырька» или «пузырьковой сортировкой»
Слайд 20алг.Сортировка обменом. Метод «Пузырька»
begin k := 0;
for i :=
1 to n-1 do{кол-во повторений}
begin
for j := 1
to n-1 do
begin
if Mass [j] > Mass [j + 1] then {Если 2 соседа нарушают }
begin rab := Mass[j]; {порядок возрастания, то }
Mass[j] := Mass[j + 1]; {производится их обмен }
Mass[j + 1] := rab; { }
k := k + 1; {к - счетчик обменов }
end; { }
end;
sss := ''; {Вывод }
for rab := 1 to Dreal do {текущего }
begin sss := sss + intToStr(Mass[rab]) + ' '; {состояния }
end; {массива }
ListBox3.Items.Add(sss); {в список }
ListBox3.ItemIndex := ListBox3.Count - 1; {ListBox3 }
sleep(5000); {Задержка }
end;
ListBox3.Items.Add('OK ! Перестановок= ' + intToStr(k)); {Вывод "OK"}
end;
Слайд 21СОРТИРОВКА ВСТАВКАМИ
При сортировке вставками(включениями) из неупорядочен-ной последовательности элементов поочередно выбирается
каждый элемент, сравнивается с предыдущим (уже упорядоченным) списком и помещается
на соответствующее место в нем.
В данном примере жирным выделен очередной элемент, а стрелкой- место для его размещения. На второй строке –вид массива после очередного перемещения.
1-й этап: 38 12 80 15 36 23 74 62
12 38 80 15 36 23 74 62
2-й этап: 12 38 80 15 36 23 74 62
12 38 80 15 36 23 74 62
3-й этап: 12 38 80 15 36 23 74 62
12 15 38 80 36 23 74 62
Слайд 22
4-й этап: 12 15 38 80 36 23 74 62
12 15
36 38 80 23 74 62
5-й этап: 12 15 36 38 80 23 74 62
12 15 23 36 38 80 74 62
6-й этап: 12 15 23 36 38 80 74 62
12 15 23 36 38 74 80 62
7-й этап:
12 15 23 36 38 74 80 62
12 15 23 36 38 62 74 80
Слайд 23алг.Сортировка вставками(включениями)
ListBox3.Items.Add(intToStr(Mass[1])); {Вывод 1-го массив состоит из 1 элемента}
ListBox3.ItemIndex
:= ListBox3.Count - 1; {вывод текущего массива }
sleep(5000);
{Задержка }
for i := 2 to Dreal do
Begin {i - номер элемента, который }
for j := 1 to i - 1 do {вставляется в растущий массив }
begin if Mass [j] > Mass [i] then {Поиск номера элемента, }
begin rab := Mass [i]; {который больше вставляемого }
for k := i - 1 downto j do {Если такой элемент найден, }
begin {то на его место вставляем }
Mass[k + 1] := Mass[k]; {i-й элемент, а остальные }
end; {сдвигаем на 1 позицию вправо }
Mass[j] := rab; goto Lab1 { }
end; { }
end;
Lab1: sss := ''; {Вывод }
for rab := 1 to i do {текущего }
begin sss := sss + intToStr(Mass[rab]) + ' '; {состояния }
end; {массива }
ListBox3.Items.Add(sss); {в список }
ListBox3.ItemIndex := ListBox3.Count - 1; {ListBox3 }
sleep(5000); {Задержка }
end;
ListBox3.Items.Add('OK !');
end;
end;
end;
end;
Слайд 24«Даже если бы сортировка была почти бесполезна, нашлась бы масса
причин заняться ею!
Изобретательные методы сортировки говорят о том, что
она и сама по себе интересна как объект исследования.»
Д.Кнут
Слайд 25ЛИТЕРАТУРА:
Е.В.Андреева Л.Л.Босова И.Н.Фалина
«Математические основы информатики»
2. Д.М.Златопольский
«Программирование:
типовые задачи, алгоритмы, методы»
3. И.Г.Семакин
«Информатика» учебник
для 10 класса профильный курс
4. И.Г.Семакин А.П.Шестаков
«Основы программирования»








![Сортировка массивов в среде DELPHI - LAZARUS 10 класс алг.Сортировка подсчетом {подсчитываем значение k [i] для каждого элемента массива a} алг.Сортировка подсчетом {подсчитываем значение k [i] для каждого элемента массива a} нц для I от 1](/img/tmb/4/383459/b4fa9ab00879c898d8e82cc6ac8720e2-800x.jpg)

![Сортировка массивов в среде DELPHI - LAZARUS 10 класс алг.Сортировка выбором {Находим минимальный элемент массива и его индекс} min:=a[1] indmin:= алг.Сортировка выбором {Находим минимальный элемент массива и его индекс} min:=a[1] indmin:= 1 нц для](/img/tmb/4/383459/869146e3ccaaf28ba79673c2decbcbc3-800x.jpg)







![Сортировка массивов в среде DELPHI - LAZARUS 10 класс алг.Сортировка вставками(включениями) ListBox3.Items.Add(intToStr(Mass[1])); {Вывод 1-го массив состоит из 1 элемента}ListBox3.ItemIndex := алг.Сортировка вставками(включениями) ListBox3.Items.Add(intToStr(Mass[1])); {Вывод 1-го массив состоит из 1 элемента}ListBox3.ItemIndex := ListBox3.Count - 1; {вывод текущего массива](/img/thumbs/e07a79c2fa5c6906832b3f8cf1a24442-800x.jpg)





















