Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Визуализация результатов расчетов в Scilab. Построение двух- и трехмерных графиков в Scilab. Функции plot, plot2d, plot3d, contour, contourf.
Содержание
- 1. Визуализация результатов расчетов в Scilab. Построение двух- и трехмерных графиков в Scilab. Функции plot, plot2d, plot3d, contour, contourf.
- 2. ScilabScilab (/ˈsaɪlæb/) — пакет прикладных математических программ,
- 3. Построение графиков функций одной переменнойПостроение графика синусоиды.
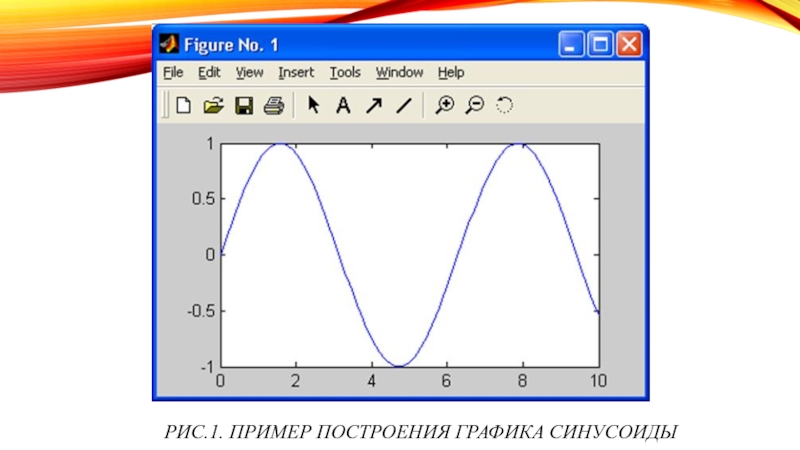
- 4. Рис.1. Пример построения графика синусоиды
- 5. Графики в полярной системе координатПостроить графики функций
- 6. графики функций y=sin(x) и y1=cos(x)
- 7. Построение графиков трехмерных поверхностейДля построения трехмерных графиков
- 8. Значения параметра type0 - применяется способ масштабирования,
- 9. Пример построения сферыСферу можно построить так:u =
- 10. Оформление и комбинирование графиковПосле того, как график
- 11. Для создания легенды используются различные варианты команды
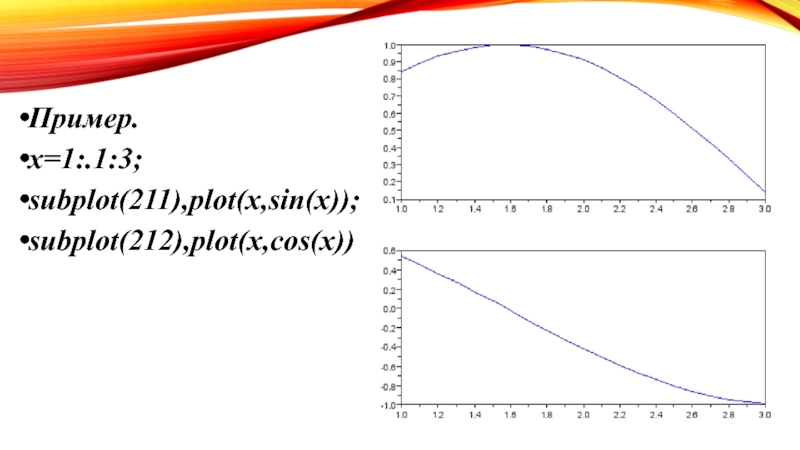
- 12. Пример.x=1:.1:3;subplot(211),plot(x,sin(x));subplot(212),plot(x,cos(x))
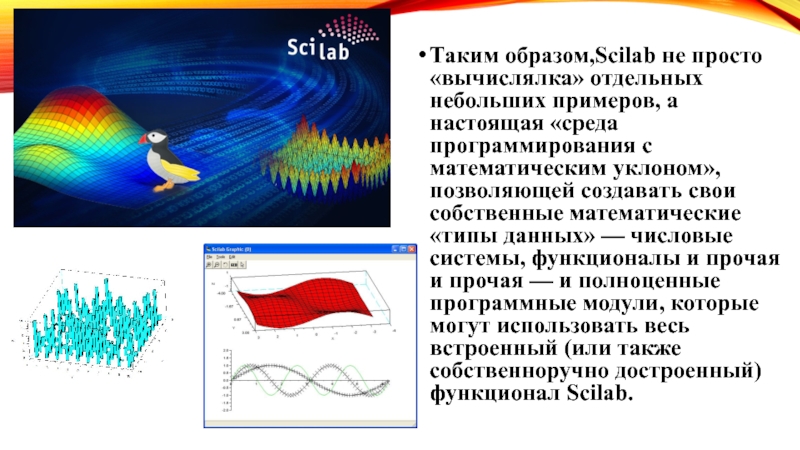
- 13. Таким образом,Scilab не просто «вычислялка» отдельных небольших
- 14. Скачать презентанцию
ScilabScilab (/ˈsaɪlæb/) — пакет прикладных математических программ, предоставляющий открытое окружение для инженерных (технических) и научных расчётов. Это самая полная общедоступная альтернатива MATLAB.
Слайды и текст этой презентации
Слайд 1
Выполнил: студент группы МДМ-115
физико-математического факультета
Якимкина Ирина
Проверила: Кормилицына Т.В.
Визуализация результатов расчетов
Слайд 2Scilab
Scilab (/ˈsaɪlæb/) — пакет прикладных математических программ, предоставляющий открытое окружение
для инженерных (технических) и научных расчётов. Это самая полная общедоступная
альтернатива MATLAB.Слайд 3Построение графиков функций одной переменной
Построение графика синусоиды. Следует помнить, что
MATLAB (как и другие СКМ) строит графики функций по ряду
точек, соединяя их отрезками прямых, т. е. осуществляя линейную интерполяцию функции в интервале между смежными точками. Зададим интервал изменения аргумента х от 0 до 10с шагом 0.1. Для построения графика достаточно вначале задать вектор х=0:0.1:10, а затем использовать команду построения графиков plot(sin(x)). Это показано на рис. 3.1.Вектор х задает интервал изменения независимой переменной от 0 до 10 с шагом 0.1. Почему взят такой шаг, а не, скажем, 1? Дело в том, что plot строит не истинный график функции sin(x), а лишь заданное числом элементов вектора х число точек. Эти точки затем просто соединяются отрезками прямых, т. е. осуществляется кусочно-линейная интерполяция данных графика. При 100 точках полученная кривая глазом воспринимается как вполне плавная, но при 10-20 точках она будет выглядеть состоящей из отрезков прямых.
Графики MATLAB строит в отдельных окнах, называемых графическими окнами. С первого взгляда видны отличия графического окна, показанного на рис. 3.1, от командного окна MATLAB. В главном меню окна появилась позиция Tools (Инструменты), которая позволяет вывести или скрыть инструментальную панель, видимую в верхней части окна графики на рис. 1. Средства этой панели (мы их рассмотрим полнее в дальнейшем) позволяют легко управлять параметрами графиков и наносить на них текстовые комментарии в любом месте.
Слайд 5Графики в полярной системе координат
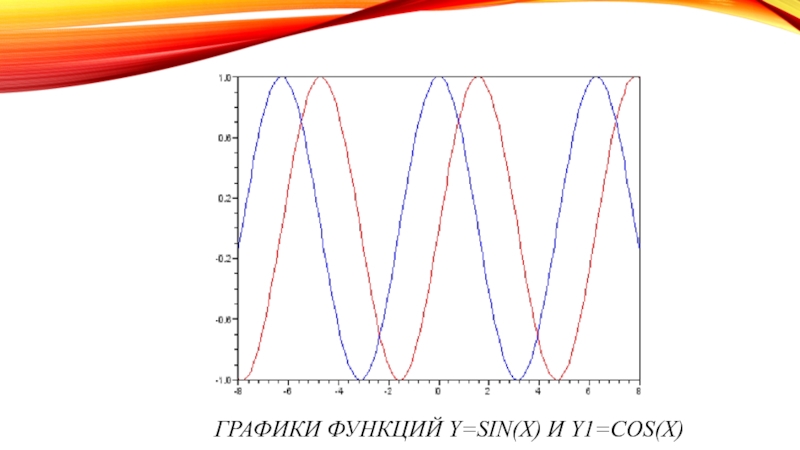
Построить графики функций y=sin(x) и y1=cos(x)
. Модифицировать масштаб координатных осей графика.
Сформируем массив Х приняв, что
х изменяется в диапазоне [-8:8] с шагом 0,1, затем совместно сформируем массивы значений заданных функций с помощью следующей записи y=[sin(x); cos(x)].С помощью функции plot2d построим графики функций y=sin(x) и y1=cos(x), установив значение параметра nax=[4,9,3,6]. Таким образом, ось X будет разбита 9 основными делениями (засечками), каждое основное 4 промежуточными, а ось Y соответственно - 6 и 3 (см. рис.).
x=[-8:0.1:8];
y=[sin(x); cos(x)];
plot2d(x,y',style=[color("red"),color("blue")],axesflag=1, nax=[4,9,3,6]);
axesflag - значение параметра keyn=valuen функции plot2d - определяет наличие рамки вокруг графика. Необходимо выделить следующие базисные значения этого параметра:
0 - нет рамки, нет изображения осей;
1 или 4 - изображение рамки, ось y слева (по умолчанию);
2 - изображение рамки, изображения осей нет;
3 - изображение рамки нет, ось y справа;
5 - изображение осей, проходящих через точку (0,0).
Слайд 7Построение графиков трехмерных поверхностей
Для построения трехмерных графиков используют операторы plot3d,
plot3d1 иmesh.
Обращение к ним следующее:
plot3d(x,y,z,[theta,alpha,leg,flag,ebox][keyn=valuen]),
plot3d1(x,y,z,[theta,alpha,leg,flag,ebox][keyn=valuen])
Здесь x - вектор - столбец
значений абсцисс;y - вектор - столбец значений ординат;
z - матрица значений функции;
theta, alpha - действительные числа, которые определяют в градусах сферические координаты угла зрения на график. Попросту говоря, это угол, под которым наблюдатель видит отображаемую поверхность;
leg - подписи координатных осей графика - символы, отделяемые знаком @. Например , 'X@Y@Z'.
flag – массив, состоящий из 3 целочисленных параметров [mode,type,box]. Здесьmode устанавливает цвет поверхности.
Значения параметра mode
>0 - поверхность имеет цвет «mode», выводится прямоугольная сетка.
0 - выводится прямоугольная сетка, заливка отсутствует (белый цвет).
<0 - поверхность имеет цвет «mode», отсутствует прямоугольная сетка.
По умолчанию, равен 2 - цвет заливки синий, прямоугольная сетка выводится.
type - позволяет управлять масштабом графика, по умолчанию имеет значение 2.
Слайд 8Значения параметра type
0 - применяется способ масштабирования, как у ранее
созданной графики.
1 - границы графика указываются вручную с помощью параметра
ebox.2 - границы графика определяют исходные данные.
Box - определяет наличие рамки вокруг отображаемого графика. По умолчанию равен 4.
Значения параметра box
0 и 1 - нет рамки
2 - только оси, находящиеся за поверхностью
3 - выводится рамка и подписи осей
4 - выводится рамка, оси и их подписи.
ebox - определяет границы области, в которую будет выводиться поверхность, как вектор [xmin,xmax,ymin,ymax,zmin,zmax]. Этот параметр может использоваться только при значении параметра type=1.
keyn=valuen - последовательность значений свойств графикаkey1=value1,key2=value2,...,keyn=valuen, таких как толщина линии, ее цвет, цвет заливки фона графического окна, наличие маркера и др. Таким образом, функцииplot3d (plot3d1) в качестве параметров необходимо передать прямоугольную сетку и матрицу значений в узлах сетки.
Слайд 9Пример построения сферы
Сферу можно построить так:
u = linspace(-%pi/2,%pi/2,40);
v = linspace(0,2*%pi,20);
X
= cos(u)'*cos(v);
Y = cos(u)'*sin(v);
Z = sin(u)'*ones(v);
plot3d2(X,Y,Z);
Оператор v = linspace(0,2*%pi,20);задает вектор
v, состоящий из 20 значений с шагом π/10.Замена последней строки программы на plot3d3(X,Y,Z); дает
Слайд 10Оформление и комбинирование графиков
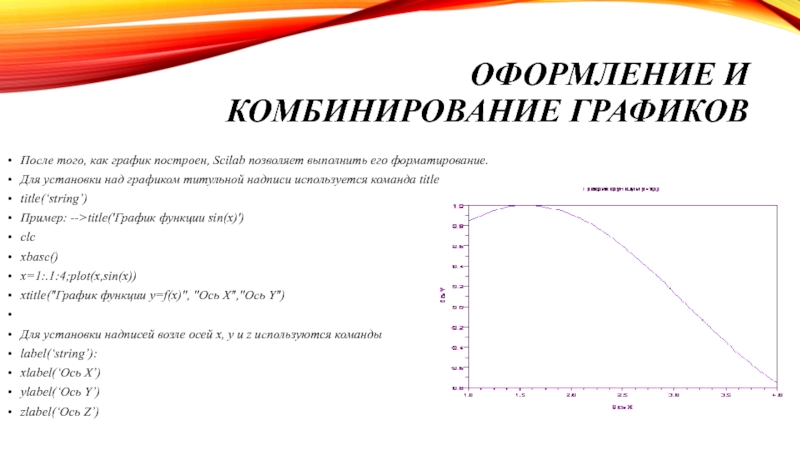
После того, как график построен, Scilab позволяет
выполнить его форматирование.
Для установки над графиком титульной надписи используется команда
titletitle(‘string’)
Пример: -->title('График функции sin(x)')
clc
xbasc()
x=1:.1:4;plot(x,sin(x))
xtitle("График функции y=f(x)", "Ось X","Ось Y")
Для установки надписей возле осей x, y и z используются команды
label(‘string’):
xlabel(‘Ось Х’)
ylabel(‘Ось Y’)
zlabel(‘Ось Z’)
Слайд 11Для создания легенды используются различные варианты команды legend.
Одна из них:
legend([‘string1’,’string2’,’string3’,….],a=pos)
Если
pos=1, то легенда помещается в верхний правый угол,
pos=2, то в
левый верхний угол,pos=3, то в левый нижний угол,
pos=4, то в нижний правый угол,
pos=5, легенда перетаскивается мышью.
Пример: -->legend(['sin(x)';'cos(x)';'sin(x)'],a=3);
Для расположения нескольких графиков в одном окне без наложения их друг на друга используется команда subplot. Она должна стоять до оператора построения графика.
subplot(m,n,p) или subplot(mnp) : m окон по горизонтали, n – по вертикали, p – номер окна, в которое будет выводиться текущий график (нумерация ведется по строкам).
clf reset удаляет все подокна и возвращают графическое окно в обычное положение.




![Визуализация результатов расчетов в Scilab. Построение двух- и трехмерных графиков в Scilab. Функции plot, plot2d, plot3d, contour, contourf. Построение графиков трехмерных поверхностейДля построения трехмерных графиков используют операторы plot3d, plot3d1 Построение графиков трехмерных поверхностейДля построения трехмерных графиков используют операторы plot3d, plot3d1 иmesh.Обращение к ним следующее:plot3d(x,y,z,[theta,alpha,leg,flag,ebox][keyn=valuen]),plot3d1(x,y,z,[theta,alpha,leg,flag,ebox][keyn=valuen])Здесь x -](/img/thumbs/91bf8ae5808a40351a41486dcb17bb66-800x.jpg)


![Визуализация результатов расчетов в Scilab. Построение двух- и трехмерных графиков в Scilab. Функции plot, plot2d, plot3d, contour, contourf. Для создания легенды используются различные варианты команды legend.Одна из них:legend([‘string1’,’string2’,’string3’,….],a=pos)Если pos=1, Для создания легенды используются различные варианты команды legend.Одна из них:legend([‘string1’,’string2’,’string3’,….],a=pos)Если pos=1, то легенда помещается в верхний правый](/img/tmb/5/443606/901cd0a5de25202680b1ab699c1a6016-800x.jpg)