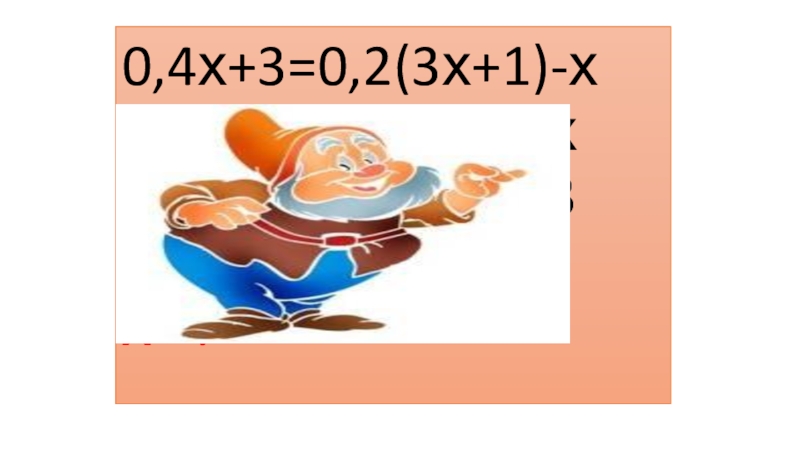Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Бир белгисиздүү сызыктуу теңдеме
Содержание
- 1. Бир белгисиздүү сызыктуу теңдеме
- 2. Кайталоо үчүн суроолор.1. Бир өзгөрмөлүү теңдеме
- 3. Кайталоо үчүн суроолор.4. Эгерде теңдеменин эки жагын
- 4. Кайталоо үчүн суроолор.6. Кашаанын алдында минус белги
- 5. х кгх кгх кгх кгх кгх кгх
- 6. Тендеменин тамырын тапкыла:х + 37 = 85х3785=_х = 4819.04.2012www.konspekturoka.ruТеңдемени чыгаруу–теңдемени туура барабардыкка айландырган өзгөрмөнүн маанисин табуу
- 7. Теңдемени чыгарбай туруп төмөнкү сандардын кайсынысы теңдеменин тамыры болоорун текшергиле42;0;14;1287 + (32 – х) = 10519.04.2012
- 8. 42;0;14;1287 + (32 – 14) = 10587
- 9. Мое кредо:Будь терпелив
- 10. Теңдеме түшүнүгүн кеңири түшүнүү.Сызыктуу теңдеме жана алардын чыгарылыштары менен таанышуу.Теңдеме жана теңдеменин жардамы менен маселелерди чыгаруу.
- 11. aх = b формуласы менен
- 12. 5 (11 – х) = 2055 –
- 13. Теңдемелерди чыгаргыла 1) 2(3х - 1) =
- 14. 2(3х - 1) = 4(х +
- 15. Теңдеменин тамыры жок 2(3х - 1) =
- 16. Теңдеме х=0 деген гана тамырга ээ3 –
- 17. Теңдеменин тамыры каалагандай сан4 – учур: Теңдемени
- 18. 1) а≠0,b≠0 х=в:а деген бир тамырга
- 19. Бир сан ойлон, ал санды
- 20. 20х+40х=240100у+6у-2у=8168,8х-1,6х=72Ортодогу сандар кайсы теңдеменин чыгарылышы болуп эсептелет?4108
- 21. Кыскача көбөйтүүнүн формуласын пайдаланып,
- 22. 3(2х – 4) – 2(х + 3) = –2+8xТеңдемени чыгаргыла:6х-12-2х-6=-2+8х4х-18=-2+8х4х-8х=-2+18-4х=16х=16:(-4)х=-4
- 23. Доскага кандайдыр бир сан жазылган. Бир окуучу
- 24. Эки жумушчу 86 тетик даярдаган.
- 25. Туулган күнүңдүн числосун ал, ага
- 26. Логикалык маселелер1. Сан жана анын жарымы 9
- 27. Тендемелерди чыгаргыла. 1. 5 (3х+1,2)+х=6,8 15х+6+х=6,8 16х=6,8-6 16х=0,8 х=0,05
- 28. Тендемелерди чыгарылышы. 1. 5 (3х+1,2)+х=6,8
- 29. 8.-(2х-12)+(6х+48)=160 -2х+12+6х+48=160
- 30. 8.-(2х-12)+(6х+48)=160 -2х+12+6х+48=160
- 31. 0,4х+3=0,2(3х+1)-х 0,4х+3=0,6х+0,2-х 0,4х+х-0,6х=0,2+3 0,8х=3,2 х=4
- 32. 0,4х+3=0,2(3х+1)-х 0,4х+3=0,6х+0,2-х 0,4х+х-0,6х=0,2+3 0,8х=3,2 х=4
- 33. Тендеменин чыгаруунун алгоритмин атагыла.* 97х + 27 = 6х + 45х = 18
- 34. Тендеменин жообун текшергиле ! (5 х-5)(х
- 35. 12(х - 2) = 3(2х - 8)+912х
- 36. « Ким биринчи» оюну. Өз алдынча иштөө:3(х
- 37. Рефлексия Жыйынтык чыгарууКелгиле суроолорго жооп беребиз:- Бүгүнкү сабакта кайталадым…- бүгүнкү сабакта бышыктадым…- бүгүнкү сабакта билдим….
- 38. Азаматсыңар силерге ийгилик!
- 39. Слайд 39
- 40. Скачать презентанцию
Кайталоо үчүн суроолор.1. Бир өзгөрмөлүү теңдеме деген эмне?2. Теңдеменин чыгарылышы деген эмне?3. Кандай теңдеме тең күчтүү теңдеме деп аталат?Жалгыз гана өзгөрмөнү камтыган барабардык бир өзгөрүлмөлүү же бир белгисиздүү теңдеме деп
Слайды и текст этой презентации
Слайд 2Кайталоо үчүн суроолор.
1. Бир өзгөрмөлүү теңдеме деген эмне?
2. Теңдеменин
чыгарылышы деген эмне?
3. Кандай теңдеме тең күчтүү теңдеме деп аталат?
Жалгыз
гана өзгөрмөнү камтыган барабардык бир өзгөрүлмөлүү же бир белгисиздүү теңдеме деп аталат. Теңдемени туура барабардыкка айландыруучу белгисиздин мааниси теңдеменин тамыры же чыгарылышы деп аталат.
Бирдей тамырларга ээ болгон теңдемелер тең күчтүү теңдемелер деп аталат.
Слайд 3Кайталоо үчүн суроолор.
4. Эгерде теңдеменин эки жагын тең бирдей санга
көбөйтсөк же бөлсөк анда кандай теңдеме пайда болот?
5. Теңдеменин мүчөлөрүн
анын бир жагынан экинчи жагына алып өткөндө кандай белги менен алып өтөбүз.Берилген теңдемеге тең күчтүү теңдеме болот
Карама-каршы белги менен алып өтүү операциясы аткарылат.
Слайд 4Кайталоо үчүн суроолор.
6. Кашаанын алдында минус белги болсо, кашааны кантип
ачабыз?
7. (а+в)(а-в)- көбөйтүндүсүн жазгыла?
8. Бөлүмдөрү ар башка болгон бөлчөктөрдү кантип
кошобуз?Карама-каршы белги менен.
а2-в2
Бирдей бөлүмгө келтирип, кошобуз.
Слайд 5х кг
х кг
х кг
х кг
х кг
х кг
х кг
Бир дарбыздын салмагы
канча экен?
5х = 2х + 6
5х -2х = 6
3х =
6х = 2
Слайд 6Тендеменин тамырын тапкыла:
х + 37 = 85
х
37
85
=
_
х = 48
19.04.2012
www.konspekturoka.ru
Теңдемени чыгаруу–теңдемени
туура барабардыкка айландырган өзгөрмөнүн маанисин табуу
Слайд 7Теңдемени чыгарбай туруп төмөнкү сандардын кайсынысы теңдеменин тамыры болоорун текшергиле
42;
0;
14;
12
87
+ (32 – х) = 105
19.04.2012
Слайд 842;
0;
14;
12
87 + (32 – 14) = 105
87 + (32 –
42) = 77
87 + (32 – х) = 105
87 +
(32 – 0) = 11987 + (32 – 12) = 107
х = 14
19.04.2012
Слайд 9
Мое кредо:
Будь терпелив
в ожидании
чуда
и будь готов
для встречи с ним
в каждом
ребенке!Ш.М. Амонашвили
2012-2020- жылдарга Кыргыз Республикасында билим берүүнү өнүктүрүү концепциясы өлкөнүн келечегин көрө билүүгө жана өнүгүү максаттарына негизделген, ошондой эле “Миң жылдыктын өнүгүү максаттарына” жана “Бардыгы үчүн билим берүү” глобалдык программалардын максаттарына жетишүүгө багытталган.
2012-2020- жылдарга Кыргыз Республикасында билим берүүнү өнүктүрүү концепциясы өлкөнүн келечегин көрө билүүгө жана өнүгүү максаттарына негизделген, ошондой эле “Миң жылдыктын өнүгүү максаттарына” жана “Бардыгы үчүн билим берүү” глобалдык программалардын максаттарына жетишүүгө багытталган.
2012-2020- жылдарга Кыргыз Республикасында билим берүүнү өнүктүрүү концепциясы өлкөнүн келечегин көрө билүүгө жана өнүгүү максаттарына негизделген, ошондой эле “Миң жылдыктын өнүгүү максаттарына” жана “Бардыгы үчүн билим берүү” глобалдык программалардын максаттарына жетишүүгө багытталган.
2012-2020- жылдарга Кыргыз Республикасында билим берүүнү өнүктүрүү концепциясы өлкөнүн келечегин көрө билүүгө жана өнүгүү максаттарына негизделген, ошондой эле “Миң жылдыктын өнүгүү максаттарына” жана “Бардыгы үчүн билим берүү” глобалдык программалардын максаттарына жетишүүгө багытталган.
Тема:
Бир белгисиздүү сызыктуу теңдеме
Билим берүү концепциясында – жаңы мазмундун , билим берүү түзүмүнүн жана уюштуруунун теориялык негиздемеси берилген, системадагы элементтер , байланыштар жана мамилелер, базалык процесстер жана функциялар баяндалган документ. Концепция латын тилинен алынып, “кабылдоо, түшүнүү, тутум” дегенди билдирет. Концепция Кыргыз Республикасынын Конститутициясына, “Билим берүү жөнүндө”, “Кепилденген мамлекетттик минималдык социалдык стандарттар жөнүндө ” Кыргыз Республикасынын мыйзамдарына жана башка документтерге негизденет. Бул концепция “ Кыргыз Республикасында билим берүүнүн өнүктүрүүнүн 2010- жылга чейинки концепциясы жөнүндө” Кыргыз Республикасынын Өкмөтүнүн 2002- жылдын 29 – апрелиндеги № 259 токтому менен жактырылган 2010-жылга чейин билим берүүнү өнүктүрүү концепциясында камтылган билим берүүнү реформалоо багытын улантат.
Билим берүү концепциясында – жаңы мазмундун , билим берүү түзүмүнүн жана уюштуруунун теориялык негиздемеси берилген, системадагы элементтер , байланыштар жана мамилелер, базалык процесстер жана функциялар баяндалган документ. Концепция латын тилинен алынып, “кабылдоо, түшүнүү, тутум” дегенди билдирет. Концепция Кыргыз Республикасынын Конститутициясына, “Билим берүү жөнүндө”, “Кепилденген мамлекетттик минималдык социалдык стандарттар жөнүндө ” Кыргыз Республикасынын мыйзамдарына жана башка документтерге негизденет. Бул концепция “ Кыргыз Республикасында билим берүүнүн өнүктүрүүнүн 2010- жылга чейинки концепциясы жөнүндө” Кыргыз Республикасынын Өкмөтүнүн 2002- жылдын 29 – апрелиндеги № 259 токтому менен жактырылган 2010-жылга чейин билим берүүнү өнүктүрүү концепциясында камтылган билим берүүнү реформалоо багытын улантат.
Билим берүү концепциясында – жаңы мазмундун , билим берүү түзүмүнүн жана уюштуруунун теориялык негиздемеси берилген, системадагы элементтер , байланыштар жана мамилелер, базалык процесстер жана функциялар баяндалган документ. Концепция латын тилинен алынып, “кабылдоо, түшүнүү, тутум” дегенди билдирет. Концепция Кыргыз Республикасынын Конститутициясына, “Билим берүү жөнүндө”, “Кепилденген мамлекетттик минималдык социалдык стандарттар жөнүндө ” Кыргыз Республикасынын мыйзамдарына жана башка документтерге негизденет. Бул концепция “ Кыргыз Республикасында билим берүүнүн өнүктүрүүнүн 2010- жылга чейинки концепциясы жөнүндө” Кыргыз Республикасынын Өкмөтүнүн 2002- жылдын 29 – апрелиндеги № 259 токтому менен жактырылган 2010-жылга чейин билим берүүнү өнүктүрүү концепциясында камтылган билим берүүнү реформалоо багытын улантат.
Билим берүү концепциясында – жаңы мазмундун , билим берүү түзүмүнүн жана уюштуруунун теориялык негиздемеси берилген, системадагы элементтер , байланыштар жана мамилелер, базалык процесстер жана функциялар баяндалган документ. Концепция латын тилинен алынып, “кабылдоо, түшүнүү, тутум” дегенди билдирет. Концепция Кыргыз Республикасынын Конститутициясына, “Билим берүү жөнүндө”, “Кепилденген мамлекетттик минималдык социалдык стандарттар жөнүндө ” Кыргыз Республикасынын мыйзамдарына жана башка документтерге негизденет. Бул концепция “ Кыргыз Республикасында билим берүүнүн өнүктүрүүнүн 2010- жылга чейинки концепциясы жөнүндө” Кыргыз Республикасынын Өкмөтүнүн 2002- жылдын 29 – апрелиндеги № 259 токтому менен жактырылган 2010-жылга чейин билим берүүнү өнүктүрүү концепциясында камтылган билим берүүнү реформалоо багытын улантат.
Билим берүү концепциясында – жаңы мазмундун , билим берүү түзүмүнүн жана уюштуруунун теориялык негиздемеси берилген, системадагы элементтер , байланыштар жана мамилелер, базалык процесстер жана функциялар баяндалган документ. Концепция латын тилинен алынып, “кабылдоо, түшүнүү, тутум” дегенди билдирет. Концепция Кыргыз Республикасынын Конститутициясына, “Билим берүү жөнүндө”, “Кепилденген мамлекетттик минималдык социалдык стандарттар жөнүндө ” Кыргыз Республикасынын мыйзамдарына жана башка документтерге негизденет. Бул концепция “ Кыргыз Республикасында билим берүүнүн өнүктүрүүнүн 2010- жылга чейинки концепциясы жөнүндө” Кыргыз Республикасынын Өкмөтүнүн 2002- жылдын 29 – апрелиндеги № 259 токтому менен жактырылган 2010-жылга чейин билим берүүнү өнүктүрүү концепциясында камтылган билим берүүнү реформалоо багытын улантат.
Билим берүү концепциясында – жаңы мазмундун , билим берүү түзүмүнүн жана уюштуруунун теориялык негиздемеси берилген, системадагы элементтер , байланыштар жана мамилелер, базалык процесстер жана функциялар баяндалган документ. Концепция латын тилинен алынып, “кабылдоо, түшүнүү, тутум” дегенди билдирет. Концепция Кыргыз Республикасынын Конститутициясына, “Билим берүү жөнүндө”, “Кепилденген мамлекетттик минималдык социалдык стандарттар жөнүндө ” Кыргыз Республикасынын мыйзамдарына жана башка документтерге негизденет. Бул концепция “ Кыргыз Республикасында билим берүүнүн өнүктүрүүнүн 2010- жылга чейинки концепциясы жөнүндө” Кыргыз Республикасынын Өкмөтүнүн 2002- жылдын 29 – апрелиндеги № 259 токтому менен жактырылган 2010-жылга чейин билим берүүнү өнүктүрүү концепциясында камтылган билим берүүнү реформалоо багытын улантат.
Билим берүү концепциясында – жаңы мазмундун , билим берүү түзүмүнүн жана уюштуруунун теориялык негиздемеси берилген, системадагы элементтер , байланыштар жана мамилелер, базалык процесстер жана функциялар баяндалган документ. Концепция латын тилинен алынып, “кабылдоо, түшүнүү, тутум” дегенди билдирет. Концепция Кыргыз Республикасынын Конститутициясына, “Билим берүү жөнүндө”, “Кепилденген мамлекетттик минималдык социалдык стандарттар жөнүндө ” Кыргыз Республикасынын мыйзамдарына жана башка документтерге негизденет. Бул концепция “ Кыргыз Республикасында билим берүүнүн өнүктүрүүнүн 2010- жылга чейинки концепциясы жөнүндө” Кыргыз Республикасынын Өкмөтүнүн 2002- жылдын 29 – апрелиндеги № 259 токтому менен жактырылган 2010-жылга чейин билим берүүнү өнүктүрүү концепциясында камтылган билим берүүнү реформалоо багытын улантат.
Билим берүү концепциясында – жаңы мазмундун , билим берүү түзүмүнүн жана уюштуруунун теориялык негиздемеси берилген, системадагы элементтер , байланыштар жана мамилелер, базалык процесстер жана функциялар баяндалган документ. Концепция латын тилинен алынып, “кабылдоо, түшүнүү, тутум” дегенди билдирет. Концепция Кыргыз Республикасынын Конститутициясына, “Билим берүү жөнүндө”, “Кепилденген мамлекетттик минималдык социалдык стандарттар жөнүндө ” Кыргыз Республикасынын мыйзамдарына жана башка документтерге негизденет. Бул концепция “ Кыргыз Республикасында билим берүүнүн өнүктүрүүнүн 2010- жылга чейинки концепциясы жөнүндө” Кыргыз Республикасынын Өкмөтүнүн 2002- жылдын 29 – апрелиндеги № 259 токтому менен жактырылган 2010-жылга чейин билим берүүнү өнүктүрүү концепциясында камтылган билим берүүнү реформалоо багытын улантат.
Билим берүү концепциясында – жаңы мазмундун , билим берүү түзүмүнүн жана уюштуруунун теориялык негиздемеси берилген, системадагы элементтер , байланыштар жана мамилелер, базалык процесстер жана функциялар баяндалган документ. Концепция латын тилинен алынып, “кабылдоо, түшүнүү, тутум” дегенди билдирет. Концепция Кыргыз Республикасынын Конститутициясына, “Билим берүү жөнүндө”, “Кепилденген мамлекетттик минималдык социалдык стандарттар жөнүндө ” Кыргыз Республикасынын мыйзамдарына жана башка документтерге негизденет. Бул концепция “ Кыргыз Республикасында билим берүүнүн өнүктүрүүнүн 2010- жылга чейинки концепциясы жөнүндө” Кыргыз Республикасынын Өкмөтүнүн 2002- жылдын 29 – апрелиндеги № 259 токтому менен жактырылган 2010-жылга чейин билим берүүнү өнүктүрүү концепциясында камтылган билим берүүнү реформалоо багытын улантат.
aх = b
х = b:а
Слайд 10Теңдеме түшүнүгүн кеңири түшүнүү.
Сызыктуу теңдеме жана алардын чыгарылыштары менен таанышуу.
Теңдеме
жана теңдеменин жардамы менен маселелерди чыгаруу.
Слайд 11 aх = b
формуласы менен берилген теңдеме
бир
белгисиздүү сызыктуу теңдеме
деп аталат. (мында х – өзгөрмөсүнүн даражасы
1
ге барабар, а -белгисиздин коэффициенти, b –бош мүчө деп аталат).
Слайд 125 (11 – х) = 20
55 – 5х = 20
-
5х = 20-55
-5х = -35
1. Теңдеменин эки жагындагы кашааларды ачуу
2. Теңдемедеги белгисиздерди анын бир жагына, сандарды экинчи жагына топтоо
3. Окшош мүчөлөрдү жыйноо
4. Теңдеменин эки жагын тең теңдеменин коэффициентине бөлүү
Х = -35:(-5)
Сызыктуу теңдемени чыгаруунуналгоритми
Х = 7
Слайд 13Теңдемелерди чыгаргыла
1) 2(3х - 1) = 4(х + 3)
2)
2(3х - 1) = 4(х + 3) + 2х
3) 2(3х
- 1) = 4(х + 3) – 14 - 2х 4) 4(2х - 1) = 4(х + 1) – 8 +4 х
Слайд 14 2(3х - 1) = 4(х + 3)
Теңдемени чыгарууда ага
тең күчтүү болгон улам жөнөкөй теңдемеге алып келебиз.
aх =
b Стандарттык түрү:
2(3х - 1) = 4(х + 3)
6х – 2 = 4х + 12
6х – 4х = 2 + 12
2х = 14
х = 14 : 2
х = 7
- Теңдеме бир тамырга ээ.
1 – учур: Теңдемени чыгаргыла:
Слайд 15Теңдеменин тамыры жок
2(3х - 1) = 4(х + 3)
+ 2х
Стандарттык түргө келтиребиз:
aх = b
2(3х -
1) = 4(х + 3) + 2х 6х – 2 = 4х + 12 + 2х
6х – 4x - 2х =2 + 12
0 · x =14
14 ≠ 0
(а = 0, b = 14)
2 – учур: Теңдемени чыгаргыла:
Слайд 16Теңдеме х=0 деген гана тамырга ээ
3 – учур: Теңдемени чыгаргыла:
2(3х - 1) = 4(х + 3) – 14 -
2хСтандарттык түрү:
aх = b
2(3х - 1) = 4(х + 3) – 14 - 2х
6х – 2 = 4х + 12 – 14 - 2х
6х – 4x + 2х = 2 + 12 – 14
4 x = 0
х = 0
(а ≠ 0, b = 0)
Слайд 17Теңдеменин тамыры каалагандай сан
4 – учур: Теңдемени чыгаргыла:
4(2х -
1) = 4(х + 1) – 8 +4 х
Стандарттык түрү:
aх = b 4(2х - 1) = 4(х + 1) – 8 + 4х
8х - 4 = 4х + 4 – 8 + 4х
8х – 4x - 4х = 4 + 4 – 8
0 x = 0
х = 0
(а ≠ 0, b = 0)
Слайд 181) а≠0,b≠0 х=в:а деген бир тамырга ээ болот.
2)
а=0,b≠0 . Теңдеме тамырга ээ болбойт
3) а≠0,b=0 . х=0 деген
1 тамырга ээ болот4) а=0, b=0. теңдеменин тамыры каалаган сан
болот.
Сызыктуу теңдемени чыгаруу
Слайд 19 Бир сан ойлон, ал санды өзүнө –өзүн кош,
чыккан санды 5 ге көбөйт, кайра биринчи ойлогон санына бөлүп
көй. ?
Слайд 2020х+40х=240
100у+6у-2у=816
8,8х-1,6х=72
Ортодогу сандар кайсы теңдеменин чыгарылышы болуп эсептелет?
4
10
8
Слайд 21 Кыскача көбөйтүүнүн формуласын пайдаланып,
теңдемелерди чыгаргыла. 1. 8х(1+2х)-(4х+3)(4х-3)=2х 2. (х+6)2-(х-5)(х+5)=121 3. (6х-1)(6х+1)-4х(9х+2)=-1 4.
(х-7)2+3=(х-2)(х+2)
Слайд 223(2х – 4) – 2(х + 3) = –2+8x
Теңдемени чыгаргыла:
6х-12-2х-6=-2+8х
4х-18=-2+8х
4х-8х=-2+18
-4х=16
х=16:(-4)
х=-4
Слайд 23Доскага кандайдыр бир сан жазылган. Бир окуучу ушул санды 23
кө чоңойтту, ал эми экинчиси 1 ге азайтты. Биринчисинин жыйынтыгы
экинчисинин жыйынтыгына караганда 7 эсе чоң болуп калды. Доскага кандай сан жазылган?Маселелерди чыгаргыла
Слайд 24 Эки жумушчу 86 тетик даярдаган. Анын биринчи экинчисинен
8 тетикке аз даярдаган. Ар бир жумушчу канча тетик даярдаган?
Слайд 25 Туулган күнүңдүн числосун ал, ага туулган айыңды көбөйтүп,
андан чыккан санга дагы 10ду көбөйт, 73тү кош, 5ке көбөйт
чыккан саныңды айт.
Слайд 34Тендеменин жообун текшергиле !
(5 х-5)(х – 4) =
0
0,5 х +0,6 = 1,5 х – 0,4
3 (5
– х) + 13 = 4 (3х – 8)0 ; 4
х = 1; 0,2
х = 4
Слайд 3512(х - 2) = 3(2х - 8)+9
12х - 24 =
6х - 24 + 9
12х - 6х = -15 +
24 6х = 9
х = 1,5
Тендеменин туура чыгарылышын текшергиле.
Слайд 36« Ким биринчи» оюну. Өз алдынча иштөө:
3(х - 5) =
2(х + 4)
х = 23
3(5 - х) + 13 =
4(3х - 8)х = 4
4(2х + 3) - 5(5 - 4х) = (2 - 3х)(-9)
х = -5
Слайд 37Рефлексия
Жыйынтык чыгаруу
Келгиле суроолорго жооп беребиз:
- Бүгүнкү сабакта кайталадым…
- бүгүнкү сабакта
бышыктадым…
- бүгүнкү сабакта билдим…
.
