Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Движение фигур в стереометрии
Содержание
- 1. Движение фигур в стереометрии
- 2. Движение – геометрическое преобразование, при котором сохраняются
- 3. ПОВОРОТЦЕНТРАЛЬНАЯ СИММЕТРИЯПАРАЛЛЕЛЬНЫЙ ПЕРЕНОСПОДОБИЕВЫВОДЫСПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВВиды движениЯНажмите на ссылку для перехода
- 4. ПОВОРОТПОВОРОТПоворот — частный случай движения, при котором
- 5. Центральной симметрией относительно точки A называют преобразование
- 6. Параллельный перенос ― частный случай движения, при
- 7. Подобие - биективное преобразование с особыми свойствами. ПОДОБИЕПОДОБИЕдалее
- 8. При движении три точки, лежащие на прямой,
- 9. http://ru.wikipedia.orghttp://fizika.asvu.ruЯзык науки: Пер. с англ./Предисл.Б. Д. Сергиевского. – М.: Мир, 1985Список использованных источников
- 10. Скачать презентанцию
Движение – геометрическое преобразование, при котором сохраняются расстояния между точками.Движением (или перемещением) фигуры называется такое ее отображение, при котором каждым двум ее точкам A и B соответствуют такие точки A’ и
Слайды и текст этой презентации
Слайд 2Движение – геометрическое преобразование, при котором сохраняются расстояния между точками.
Движением
(или перемещением) фигуры называется такое ее отображение, при котором каждым
двум ее точкам A и B соответствуют такие точки A’ и B’, что |A’B’| = |AB|.ОПРЕДЕЛЕНИЕ ДВИЖЕНИЯ
далее
Слайд 3ПОВОРОТ
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
ПОДОБИЕ
ВЫВОДЫ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
Виды движениЯ
Нажмите на ссылку для перехода
Слайд 4ПОВОРОТ
ПОВОРОТ
Поворот — частный случай движения, при котором по крайней мере
одна точка плоскости (пространства) остаётся неподвижной. При вращении плоскости неподвижная
точка называется центром вращения, при вращении пространства неподвижная прямая называется осью вращения. Вращение плоскости (пространства) называется собственным (вращение первого рода) или несобственным (вращение второго рода) в зависимости от того, сохраняет оно или нет ориентацию плоскости (пространства).далее
Слайд 5Центральной симметрией относительно точки A называют преобразование плоскости, переводящее точку
X в такую точку X', что A — середина отрезка
XX'. Центральная симметрия с центром в точке A обычно обозначается через ZA, в то время как обозначение SA можно перепутать с осевой симметрией.ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
далее
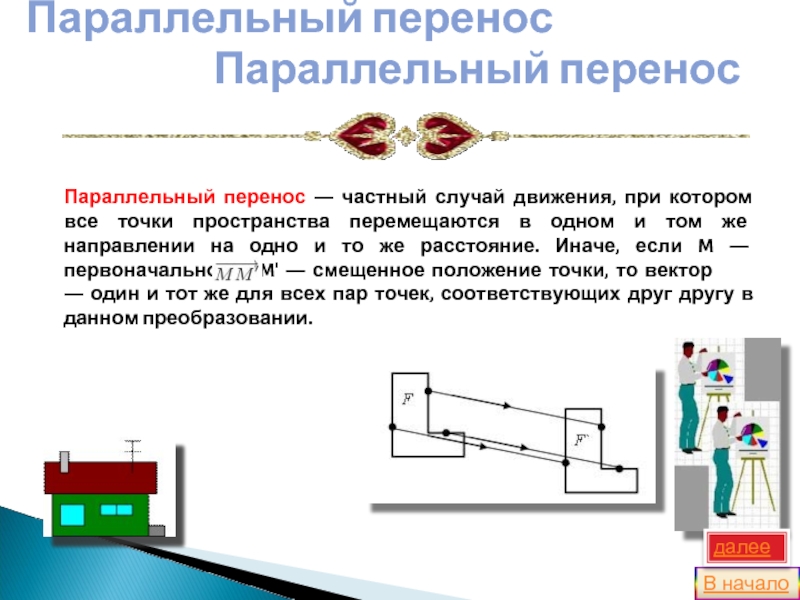
Слайд 6Параллельный перенос ― частный случай движения, при котором все точки
пространства перемещаются в одном и том же направлении на одно
и то же расстояние. Иначе, если M ― первоначальное, а M' ― смещенное положение точки, то вектор ― один и тот же для всех пар точек, соответствующих друг другу в данном преобразовании.Параллельный перенос
Параллельный перенос
далее
Слайд 8При движении три точки, лежащие на прямой, переходят в три
точки, лежащие на прямой, причем точка, лежащая между двумя другими,
переходит в точку, лежащую между образами двух других точек (сохраняется порядок их взаимного расположения).Образом отрезка при движении является отрезок.
Образом прямой при движении является прямая, а образом луча - луч.
При движении образом треугольника является равный ему треугольник, образом плоскости - плоскость, причем параллельные плоскости отображаются на параллельные плоскости, образом полуплоскости - полуплоскость.
При движении образом тетраэдра является тетраэдр, образом пространства - все пространство, образом полупространства - полупространство.
При движении углы сохраняются, т.е. всякий угол отображается на угол того же вида и той же величины. Аналогичное верно и для двугранных углов.
Выводы
далее
Слайд 9http://ru.wikipedia.org
http://fizika.asvu.ru
Язык науки: Пер. с англ./Предисл.Б. Д. Сергиевского. – М.: Мир,
1985
Список использованных источников
Теги