ЕГЭ 2020. Математика. Задачи с экономическим содержанием. Задача 17 (профильный уровень)

виде графиков, диаграмм и таблиц,
простейшие текстовые арифметические задачи на товарно-денежные

отношения (в основном на оплату товаров и услуг),
арифметические текстовые задачи на проценты,
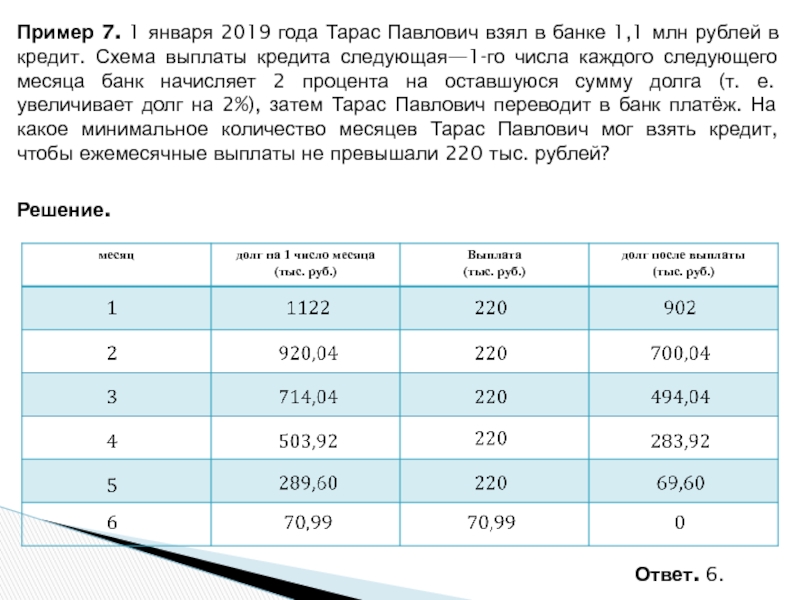
задачи о кредитовании и банковских процентах,
задачи оптимизации производства товаров или услуг (минимизации расходов или максимизации прибыли).

числа.

За 100% всегда принимают то, с чем сравнивают. Если a>b

на 20%, то a=1,2b.

Отношение показывает, какую часть от числа b составляет число a.

Выражение показывает, сколько процентов от числа b составляет число a.

увеличили на 20%, то получили 1,2А.

Число A уменьшили на 20%,

то получили 0,8А.

число b меньше a (b

кредитам

однократном изменении величины вклада на определённое число процентов (простые проценты),

либо о последовательном изменении величины вклада через (как правило) равные промежутки времени на определённое число процентов (сложные проценты). В последнем случае каждый раз начиная со второго проценты начисляются на сумму, полученную после предыдущего начисления процентов.

банке 1 сентября сроком на 1 месяц под 12% годовых.

Сколько рублей окажется на счёте вклада 1 октября того же года, если сумма вклада равна 100 000 рублей?

S0 = 100 000

r = 12

m = 30

Решение.

Ответ. 100 986,30 руб.

пролонгацией в течение нескольких раз.
Проценты на депозит начисляются несколько раз

через равные промежутки времени и каждый раз зачисляются на вклад.

значит, первый вклад выгоднее.
Ответ. Первый.

платежами процент и периодичность обязательных платежей фиксируются (например, ежегодные, ежеквартальные

или помесячные платежи), а фиксированный процент начисляется на ещё не выплаченную к моменту очередного обязательного платежа часть кредита (долга).

n лет
Клиент должен вернуть банку сумму кредита (долг) и проценты

за пользование кредитом на следующих условиях: каждый год клиент возвращает банку

1/n

часть суммы долга (кредита)

проценты за пользование кредитом, начисляемые ежегодно на остаток долга

сумма всех начисленных процентов (переплата)

сумме начисленных процентов

года под 16% годовых. На сколько процентов сумма всех выплат

банку окажется больше суммы кредита, если досрочное погашение кредита не предполагается?

Решение.

Cумма всех выплат

окажется на 40% больше суммы кредита.

k% на оставшуюся сумму долга, т. е. увеличивает её на

k%;

после начисления процентов клиент вносит в банк (также до
истечения соответствующего платёжного периода) некоторую сумму
x—одну и ту же для каждого платежа; сумма долга при этом
уменьшается, и на эту уменьшенную на x сумму начисляются проценты до истечения следующего платёжного периода, после чего клиент вносит в банк платёж в размере той же суммы x и т. п.

банке кредит на сумму 109 500 рублей под 24% годовых

сроком на 6 месяцев на условиях погашения кредита ежемесячными аннуитетными (равными) платежами.
Найдите сумму всех выплат по кредиту.

Решение.

кредит на 3 года под 10% годовых. Схема выплаты кредита

следующая: до 31 ноября каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т. е. увеличивает долг на 10%), затем до истечения этого же платёжного периода (т. е. по 31 декабря того же года) бизнесмен переводит в банк определённую (одну и ту же для каждого года) сумму ежегодного платежа. Какой была сумма кредита (в рублях), если сумма ежегодного платежа составила 2 662 000 рублей?

Решение.

x —сумма ежегодной выплаты

Суммы долга по истечении каждого платёжного периода:

Ответ. 6 620 000.

сумму 16 млн рублей на некоторый срок (целое число лет).

Условия его возврата таковы:
• каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
• с февраля по июнь каждого года необходимо выплатить часть долга;
• в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей?

Решение.

Пусть кредит планируется взять на n лет.

Долг перед банком (в млн рублей) по состоянию на июль должен уменьшаться до нуля равномерно, т. е. на 1/n -ю часть, поэтому суммы долга за каждый месяц (до начисления процентов) составят (в порядке убывания):

По условию каждый январь долг возрастает на 25%, поэтому последовательность размеров платежей по процентам будет следующей:

по процентам, поэтому ежегодные платежи составят соответственно
Общая сумма S всех

выплат

Ответ. 10.

сумму 4,5 млн рублей на срок 9 лет. Условия его

возврата таковы:
• каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
• с февраля по июнь каждого года необходимо выплатить часть долга;
• в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший—не менее 0,6 млн рублей.

Решение.

По условию долг перед банком (в млн рублей) по состоянию на июль должен уменьшаться до нуля равномерно, т. е. на 1/9 часть, поэтому суммы долга за каждый год (до начисления процентов) составят (в порядке убывания)

4,5, 4, …, 1, 0,5.

По условию каждый январь долг возрастает на r%. Поэтому последовательность размеров платежей по процентам будет следующей:

Ежегодный платёж

фиксированная сумма

сумма платежа по процентам

банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая—1-го

числа каждого следующего месяца банк начисляет 2 процента на оставшуюся сумму долга (т. е. увеличивает долг на 2%), затем Тарас Павлович переводит в банк платёж. На какое минимальное количество месяцев Тарас Павлович мог взять кредит, чтобы ежемесячные выплаты не превышали 220 тыс. рублей?

Решение.

Ответ. 6.

банке 1,1 млн рублей в кредит. Схема выплаты кредита следующая—1-го

числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (т. е. увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич мог взять кредит, чтобы ежемесячные выплаты не превышали 275 тыс. рублей?

Решение.

Александр Сергеевич

не покроет долг с процентами.

каждый месяц долг увеличивается не более чем на данную величину.

Александр Сергеевич сможет выплатить кредит за 5 месяцев.

Ответ. 5.