Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формирование математических способностей учащихся через развитие логического мышления.
Содержание
- 1. Формирование математических способностей учащихся через развитие логического мышления.
- 2. «Если хочешь увидеть результат, будь
- 3. Слайд 3
- 4. Основные
- 5. Программа факультативного курсапо математике (решение логических задач)
- 6. Цель: Организация работы с учащимися, имеющими повышенный
- 7. Содержание: Задачи
- 8. Задачи на разрезание и складывание фигур. (игра
- 9. Слайд 9
- 10. Слайд 10
- 11. В игре «Танграм» (как и в любой
- 12. Танграм развивает : фантазию, внимание, упорство, пространственное
- 13. 1.Головоломки. Их виды. 2.История возникновения игры
- 14. "Очарование танграма состоит
- 15. ГрафыЗадачи, решаемые с помощью графов.
- 16. Проведение поиска способа и осуществления решения задачи
- 17. Основные этапы при решении задач:1 этап: заключается
- 18. Что
- 19. Схема графа, состоящая из «изолированных»
- 20. Примеры графов
- 21. Дерево – это граф,
- 22. Кенигсбергские мосты
- 23. Кенигсбергские мостыМожно ли обойти все Кенигсбергские мосты, проходя только один раз через каждый из этих мостов?
- 24. Представим задачу в виде графа,где вершины –
- 25. Какие вершины четные, а какие нечетные? Подпишем
- 26. Алгоритм решения задач1. Нарисовать граф, где вершины
- 27. Слайд 27
- 28. Построим граф, где вершины – острова и
- 29. . Нечетные вершины: D, E.ВЫВОД: Так как
- 30. Решение логических задач табличным способом и с помощью графиков
- 31. - Что такое таблицы? Это
- 32. Задача № 1В школе учатся 4 талантливых
- 33. 2. Петров и музыкант вместе позировали художнику → Петров – не художник и не музыкант
- 34. 3. Музыкант раньше дружил с Андреевым, а
- 35. 4. Так как Сидоров – музыкант, он не может быть ни солистом, ни танцором, ни художником.
- 36. 4. Так как Сидоров – музыкант, он не может быть ни солистом, ни танцором, ни художником.
- 37. 5. Петров и Сидоров вместе позировали художнику,
- 38. 6. Теперь определился солист – это Петров → танцор – Иванов.
- 39. ИвановПетровСидоровАндреевМузыкантТанцорСолистХудожникРешение задач с помощью графиков :О них
- 40. Задача 2Маша, Оля, Лена и Валя –
- 41. 6. Т. к. Оля не знает английский → она говорит по-немецки → по-английски говорит Маша.
- 42. МашаОляЛенаВаляРояльСкрипкаВиолончельарфаФ. И.
- 43. Слайд 43
- 44. Слайд 44
- 45. Слайд 45
- 46. Слайд 46
- 47. Работать с одаренными,
- 48. Всем успеха!
- 49. Спасибо за просмотрСпасибо за внимание!
- 50. Скачать презентанцию
«Если хочешь увидеть результат, будь готов много работать»
Слайды и текст этой презентации
Слайд 1Формирование математических способностей учащихся через развитие логического мышления. учитель математики Абдрахмановой
С.А.
Слайд 2
«Если хочешь увидеть результат, будь готов много работать»
Мария Берсенева
«Все дети одарены от природы»
Слайд 3
Целью обучения математики в школе является
не только овладение конкретными математическими знаниями, а развитие его индивидуальных,
умственных и физических способностей, одаренности и таланта.Формирование качеств мышления, характерных для математической деятельности и необходимых человеку для продуктивной жизни в обществе.
Слайд 4
Основные формы работы учителей с одаренными детьми:
факультативы
кружки
творческие мастерские;
работа по индивидуальным
планам
занятия исследовательской деятельностью;
участие в конкурсах
научно-практические конференции;
подготовка к олимпиадам
Слайд 5
Программа факультативного курса
по математике
(решение логических задач)
Автор: учитель математики
Абдрахманова С.А.
2014-2015 уч.г.
Слайд 6Цель: Организация работы с учащимися, имеющими повышенный уровень
мотивации, включение учащихся в исследовательскую деятельность.
Задачи:
- формирование у учащихся
устойчивого интереса к математике; - выявление и развитие математических способностей;
- овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности;
- интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности;
- формирование представлений о математике как части общечеловеческой культуры, понимание значимости математики для общественного прогресса;
- подготовка к сознательному усвоению систематического курса алгебра и геометрия;
- формирование навыков перевода различных задач на язык математики.
Слайд 7 Содержание:
Задачи на разрезание и
складывание фигур. - 3
часа(игра Танграм.)
Задачи, решаемые с помощью графов. - 3 часа
Задачи с использованием таблиц и графиков. - 3 часа
Задачи с отношениями -3 часа
Задачи на переправу. - 3 часа
Задачи на проценты - 3 часа
Занимательные задачи. - 3 часа
Задачи на переливания. -3 часа
Математические игры -3 часа
Текстовые задачи -3 часа
Задачи с геометрическим содержанием -3 часа
Итоговое занятие - 1 час
Слайд 8Задачи на разрезание и складывание фигур. (игра Танграм.)
Танграм —
это, самая популярная игра из серии так называемых «геометрических конструкторов»
Слайд 11В игре «Танграм» (как и в любой другой игре) существуют
определенные правила:
В каждую собранную фигуру должны входить все семь
элементов.При составлении фигур элементы не должны налегать друг на друга.
Элементы фигур должны примыкать один к другому.
Начинать нужно с того, чтобы найти место самого большого треугольника.
Слайд 12
Танграм развивает :
фантазию, внимание, упорство,
пространственное воображение, сообразительность,
творческие
способности;
логическое мышление, наглядно-образное мышление;
внимание;
мелкую маторику;
Учит :последовательности и терпению.
умению играть по правилам и выполнять инструкции;
умению комбинировать;
усидчивости;
пониманию цвета, величины и формы.
Слайд 13 1.Головоломки. Их виды.
2.История возникновения игры «Танграм».
3. Мифы о
создании игры «Танграм».
4.«Танграм» в литературных произведениях.
5.«Танграм» Новые идеи и возможности.
Темы для исследовательских работ:
Слайд 14
"Очарование танграма состоит в простоте материала
и в кажущейся его непригодности для создания фигурок, обладающих эстетической
привлекательностью» М. ГарднераСлайд 16Проведение поиска способа и осуществления решения задачи нуждается в следующих
способностях :
абстрагирования;
моделирования,
гибкого
применения теории графов, применения всех известных математических способов решения.
Слайд 17Основные этапы при решении задач:
1 этап: заключается в том, что
бы суметь проанализировать и закодировать условия задачи.
2 этап: схематическая
запись. состоит в геометрическом представлении графов, и на этом этапе элемент творчества очень важен потому, что далеко не просто найти соответствия между элементами условия и соответствующими элементами графа.
Все остальные этапы тоже не обходятся без применения творчества и изобретательности. Слайд 18 Что такое граф?
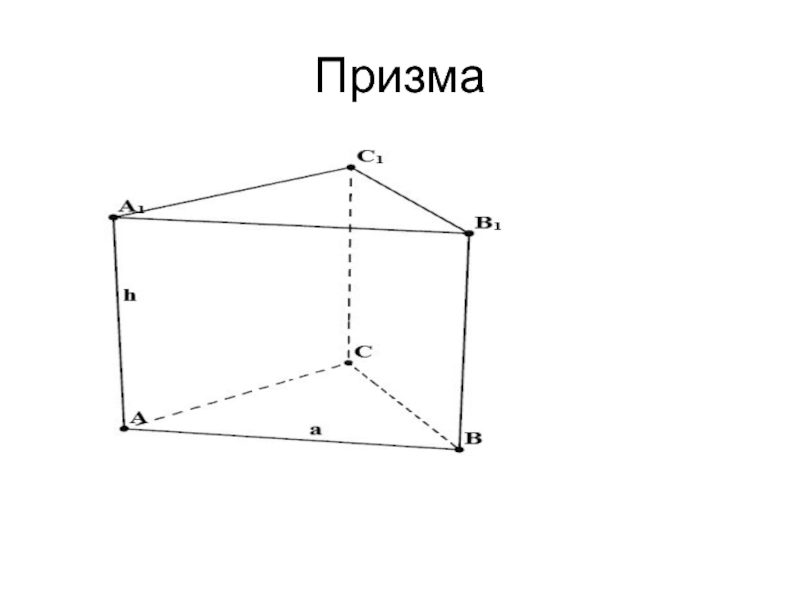
Граф- геометрическая
фигура, состоящая из точек(вершины графа) и линий , их соединяющих(рёбра
графа).Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями.
В математике определение графа дается так: графом называется конечное множество точек, некоторые из которых соединены линиями.
Слайд 19Схема графа, состоящая из
«изолированных» вершин,
называется нулевым графом
Графы, в которых не построены все
возможные ребра, называютсянеполными графами
Графы, в которых построены все
возможные ребра, называются
полными графами
Слайд 21 Дерево – это граф, в котором две любые вершины соединены
ровно одним простым путём.
код
1
2
3
2
4
3
1
2
3
4
1
2
3
4
1
2
3
4
4
Слайд 23Кенигсбергские мосты
Можно ли обойти все Кенигсбергские мосты, проходя только один
раз через каждый из этих мостов?
Слайд 24Представим задачу в виде графа,где вершины – острова и берега
(A,B,C,D), а ребра – мосты
Важно, является ли число мостов, ведущих
к этим отдельным участкам, четным или нечетным. Так, в нашем случае к участку A ведут пять мостов, а к остальным – по три моста.
Слайд 25Какие вершины четные, а какие нечетные? Подпишем степени вершин в
кружочках.
Нечетные вершины: А, B, C, D.
Вывод: нельзя
3
3
3
5
Слайд 26Алгоритм решения задач
1. Нарисовать граф, где вершины – острова и
берега, а ребра – мосты.
2. Определить степень каждой вершины
и подписать возле нее.3. Посчитать количество нечетных вершин.
4. Обход возможен:
a. ЕСЛИ все вершины – четные, и его можно начать с любого участка.
b. ЕСЛИ 2 вершины – нечетные, но его нужно начать с одной из нечетных местностей.
5. Обход невозможен, если нечетных вершин больше 2.
6. Сделать ВЫВОД.
7. Указать Начало и Конец пути.
Слайд 27
Задача о
15 мостах
В некоторой местности через протоки переброшено 15 мостов.
Можно ли обойти все мосты ,проходя по каждому мосту только один раз? Слайд 28Построим граф, где вершины – острова и берега, а ребра
– мосты.
определить степень каждой вершины и узнать какие вершины четные,
а какие нечетные. Слайд 29.
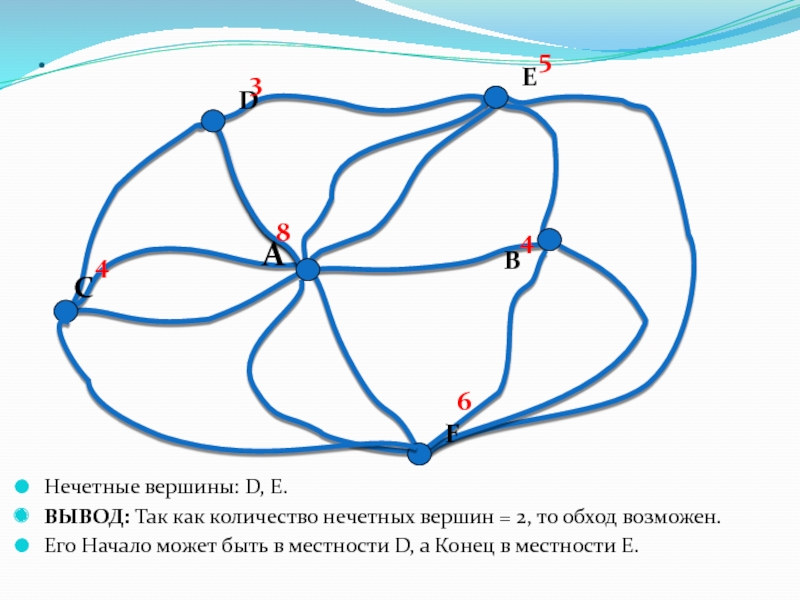
Нечетные вершины: D, E.
ВЫВОД: Так как количество нечетных вершин =
2, то обход возможен.
Его Начало может быть в местности D,
а Конец в местности E.4
4
6
3
5
8
Слайд 31- Что такое таблицы? Это форма представления информации, где
информация:
систематизирована
наглядна и емка
ее части взаимосвязаны
имеют логическую зависимость
Слайд 32Задача № 1
В школе учатся 4 талантливых мальчика: Иванов, Петров,
Сидоров и Андреев. Один из них – будущий музыкант, другой
преуспел в бальных танцах, третий – солист хора мальчиков, четвертый подает надежды как художник.О них известно следующее:
1. Иванов и Сидоров присутствовали в зале консерватории, когда там солировал в хоре мальчиков певец.
2. Петров и музыкант вместе позировали художнику.
3. Музыкант раньше дружил с Андреевым, а теперь хочет познакомиться с Ивановым.
4. Иванов не знаком с Сидоровым, т.к. они учатся в разных классах и в разные смены.
Кто чем увлекается?
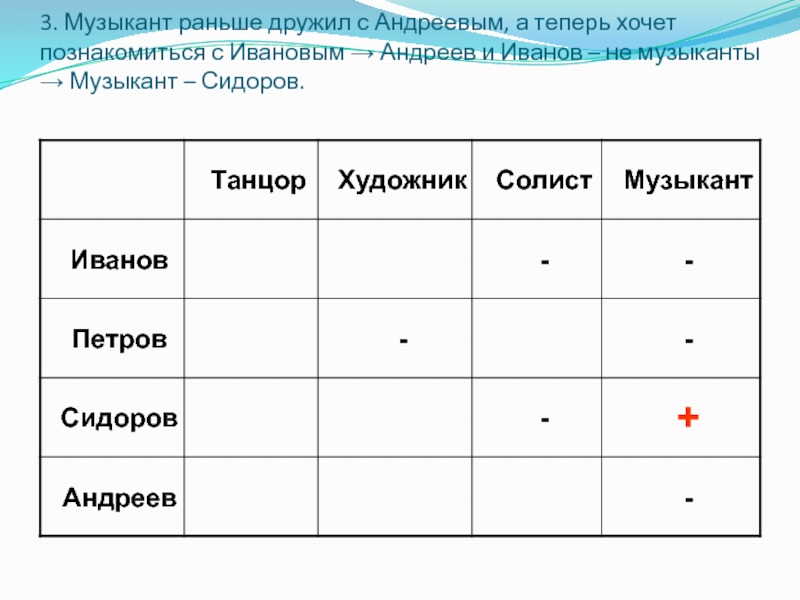
Слайд 343. Музыкант раньше дружил с Андреевым, а теперь хочет познакомиться
с Ивановым → Андреев и Иванов – не музыканты →
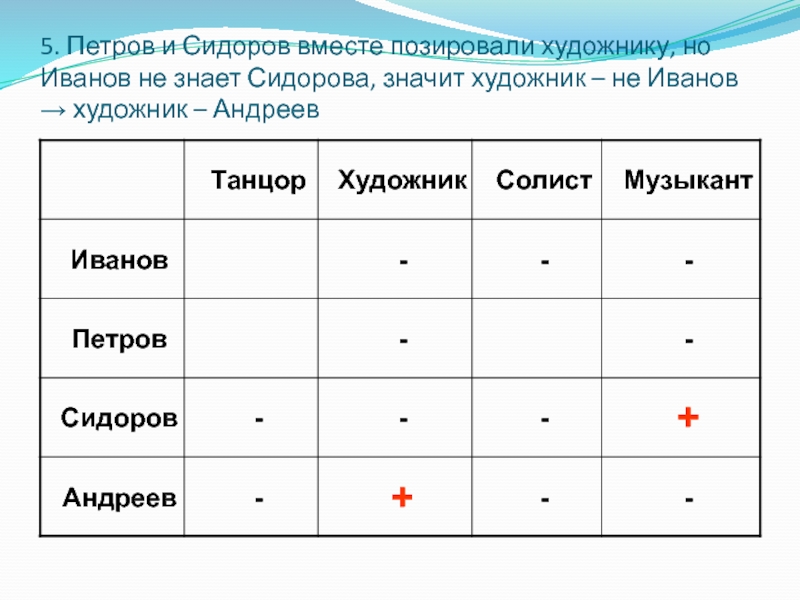
Музыкант – Сидоров.Слайд 375. Петров и Сидоров вместе позировали художнику, но Иванов не
знает Сидорова, значит художник – не Иванов → художник –
АндреевСлайд 39Иванов
Петров
Сидоров
Андреев
Музыкант
Танцор
Солист
Художник
Решение задач с помощью графиков :
О них известно следующее:
1. Иванов
и Сидоров присутствовали в зале консерватории, когда там солировал в
хоре мальчиков певец.2. Петров и музыкант вместе позировали художнику.
3. Музыкант раньше дружил с Андреевым, а теперь хочет познакомиться с Ивановым.
4. Иванов не знаком с Сидоровым, т.к. они учатся в разных классах и в разные смены.
Кто чем увлекается?