Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функционально-графический подход к решению задач.
Содержание
- 1. Функционально-графический подход к решению задач.
- 2. Цель:Обобщить и закрепить умения строить графики функций
- 3. 1). Повторение. Графики элементарных функций.Линейная функцияКвадратичная функцияДробно-линейная функцияСтепенная функцияОкружность Функция Желаю интересной работы на уроке.
- 4. k < 0k > 0bЛинейная функция y
- 5. bb > 0bb < 0y = b (k = 0) b>0, b
- 6. k < 0k > 0kk1y = kx (b = 0) k>0, k
- 7. D = b² – 4ac > 0
- 8. D = b² – 4ac < 0
- 9. D = b² – 4ac = 0
- 10. Степенная функцияСтепенная функция с натуральным показателем степени y = xⁿ, где n Є N n-чётное число.7
- 11. Степенная функцияСтепенная функция с натуральным показателем степени y = xⁿ, где n Є N n-нечётное число8
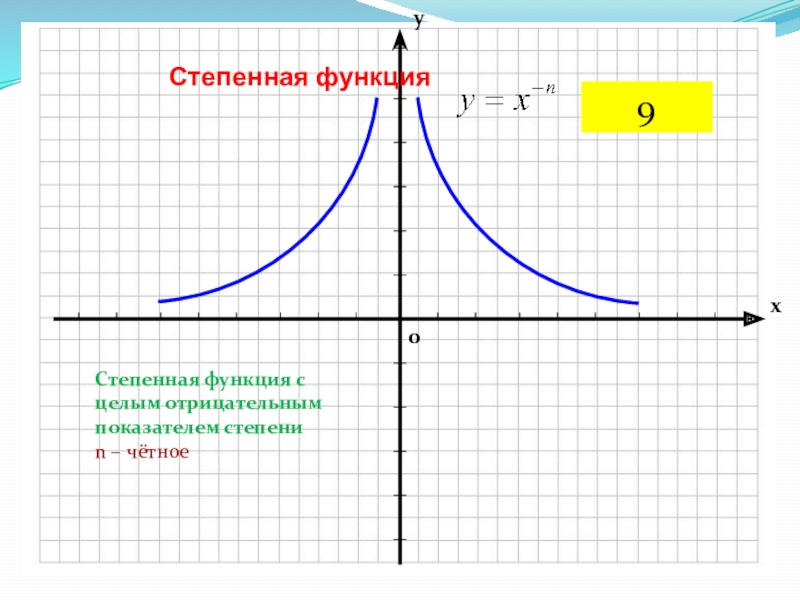
- 12. Степенная функцияСтепенная функция с целым отрицательным показателем степениn – чётное9
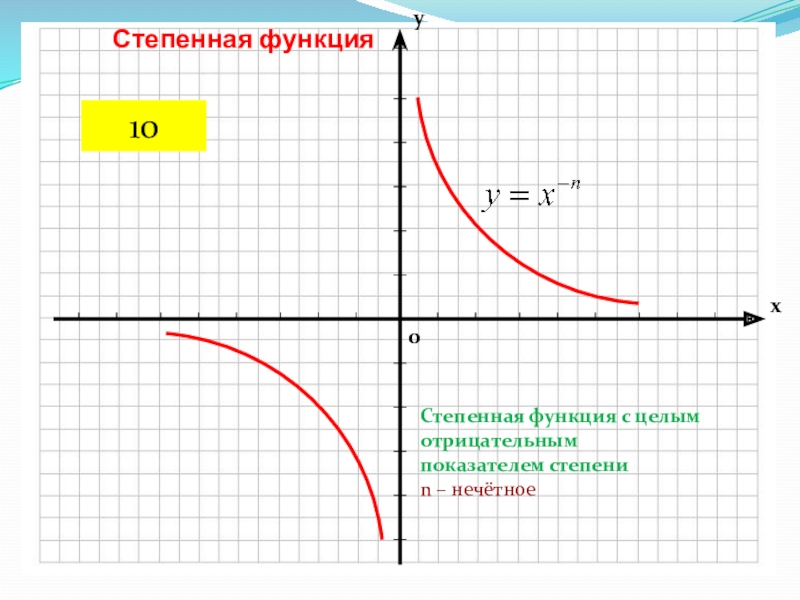
- 13. Степенная функцияСтепенная функция с целым отрицательным показателем степениn – нечётное10
- 14. k > 0k < 0График - гиперболаДробно-линейная
- 15. n – нечётноеФункция 12
- 16. n – чётноеФункция 14
- 17. Уравнение окружности.(х – а)2 + (у –
- 18. Слайд 18
- 19. «…Математика … выявляет порядок, симметрию и
- 20. 2).Повторение пройденного материала. Основные приёмы преобразования графиков.Параллельный
- 21. f(x) → f(x + а) 1. Параллельный
- 22. f(x) → f(x) + b 2. Параллельный
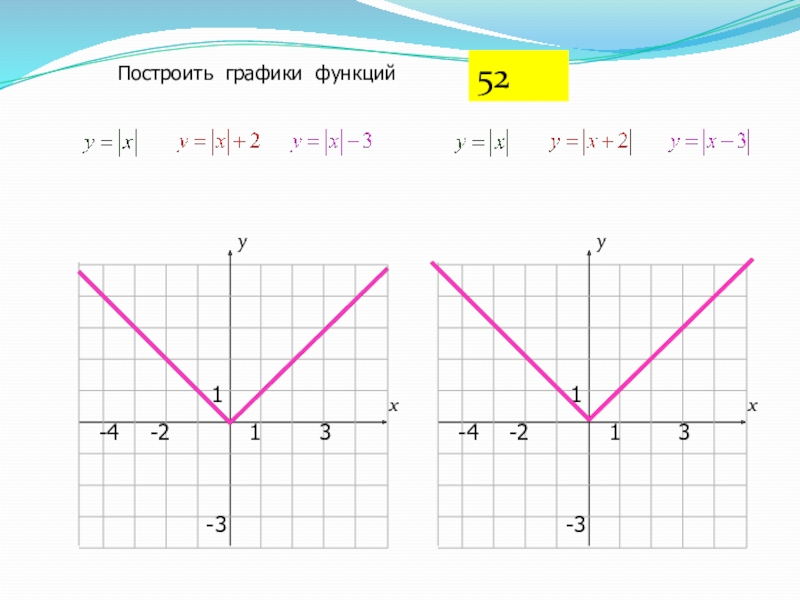
- 23. 13-41-3-2хууПостроить графики функций
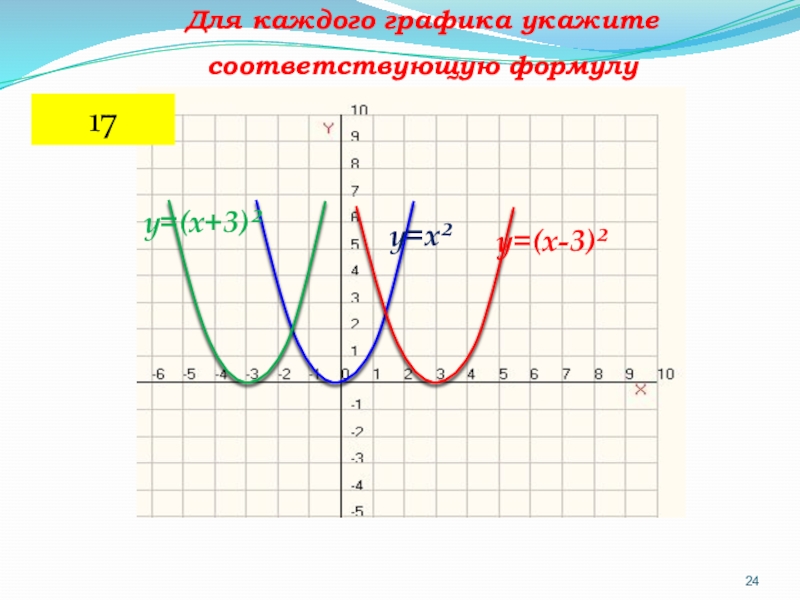
- 24. y=x²y=(x-3)²Для каждого графика укажите соответствующую формулуy=(x+3)²17
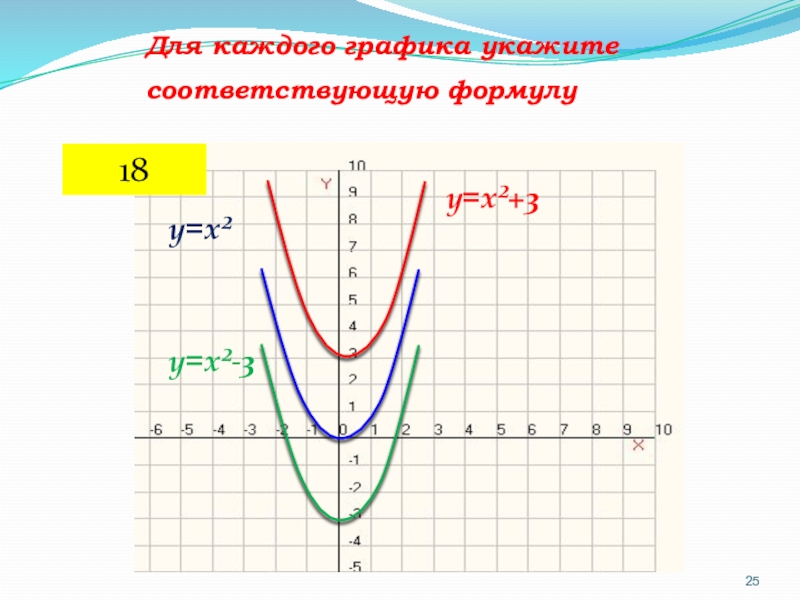
- 25. y=x²y=x²+3y=x²-3Для каждого графика укажите соответствующую формулу18
- 26. f(x) → f(кx) y=f(kx)k > 13.
- 27. 0 < k < 1 4. Растяжение
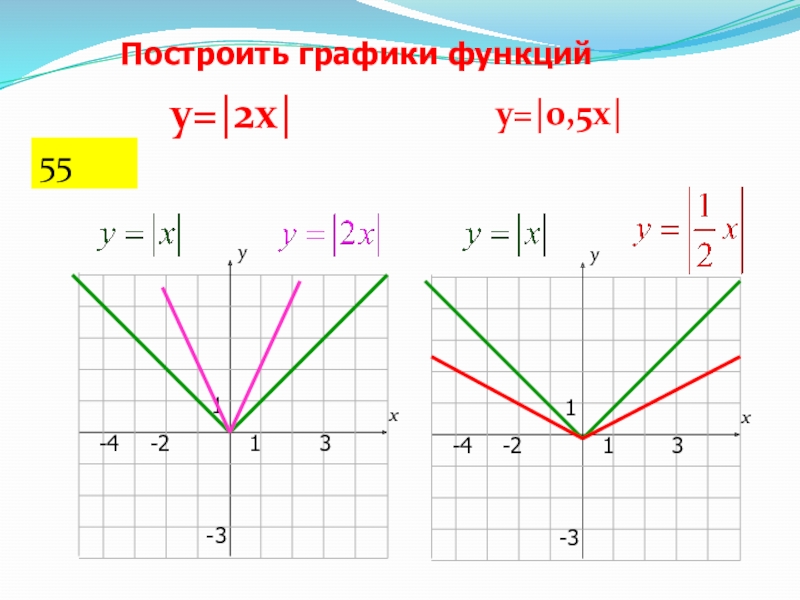
- 28. Построить графики функцийу=|2х|у=|0,5х|55
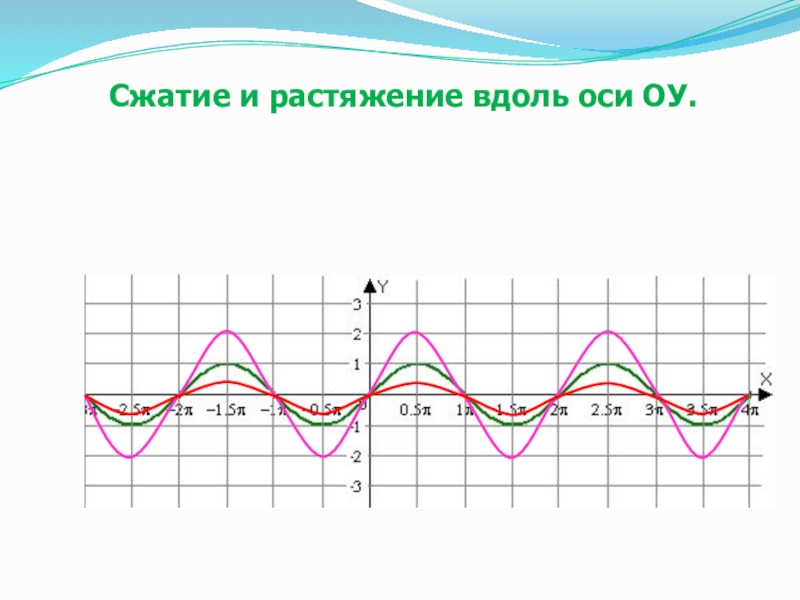
- 29. Сжатие и растяжение вдоль оси ОУ.
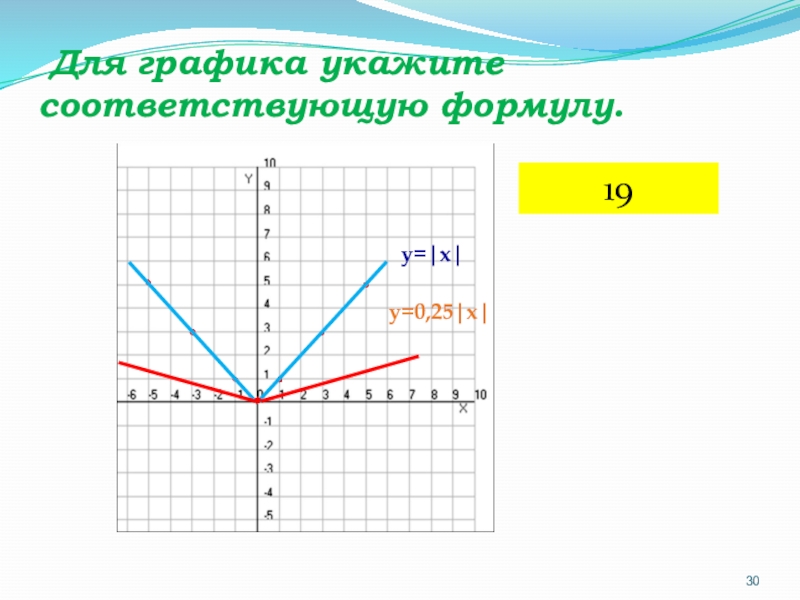
- 30. Для графика укажите соответствующую формулу.y=|x|y=0,25|x|19
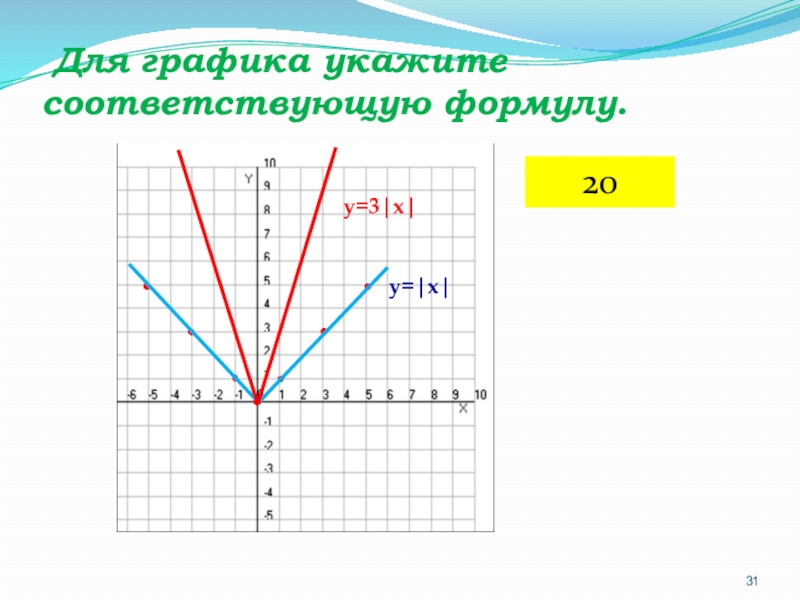
- 31. Для графика укажите соответствующую формулу.y=|x|y=3|x|20
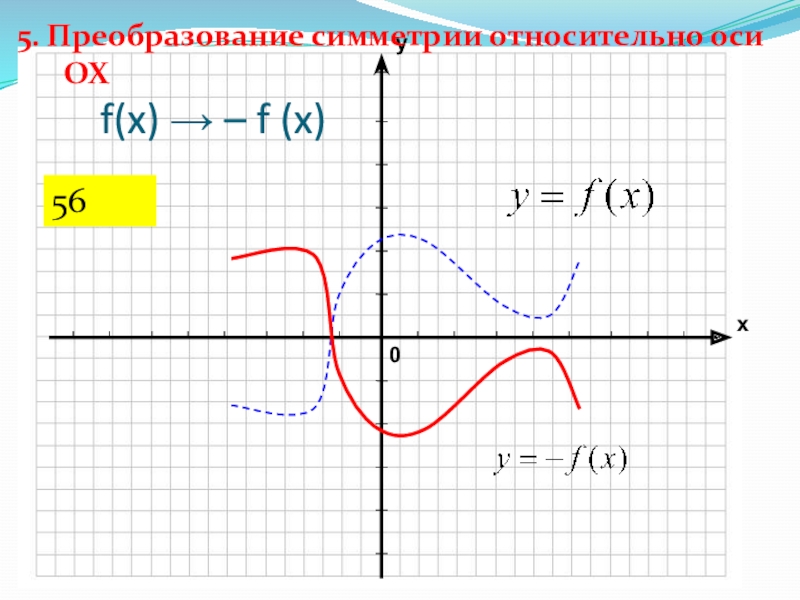
- 32. f(x) → – f (x) 5. Преобразование симметрии относительно оси ОХ56
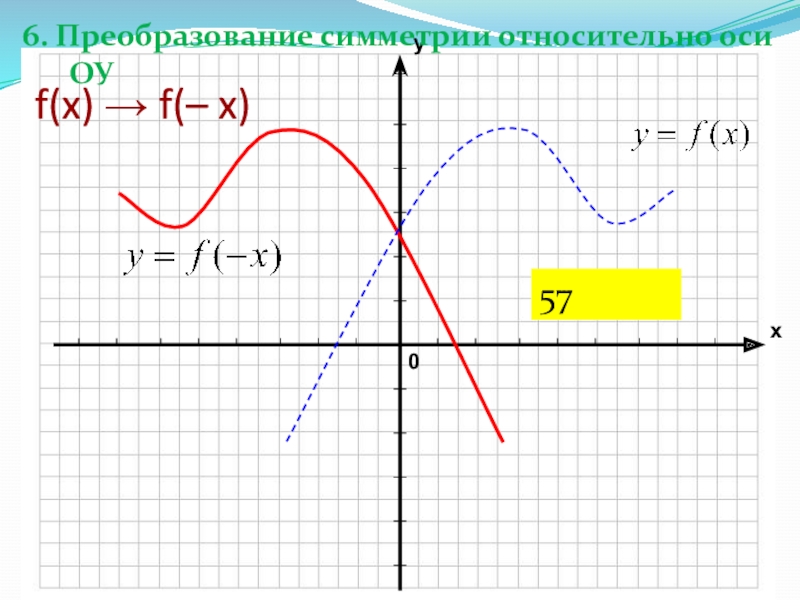
- 33. f(x) → f(– x) 6. Преобразование симметрии относительно оси ОУ57
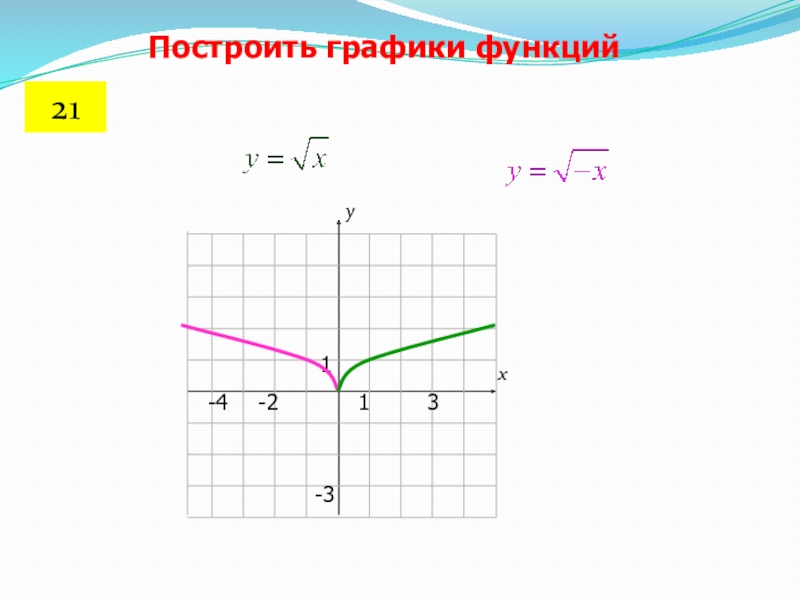
- 34. Построить графики функций21
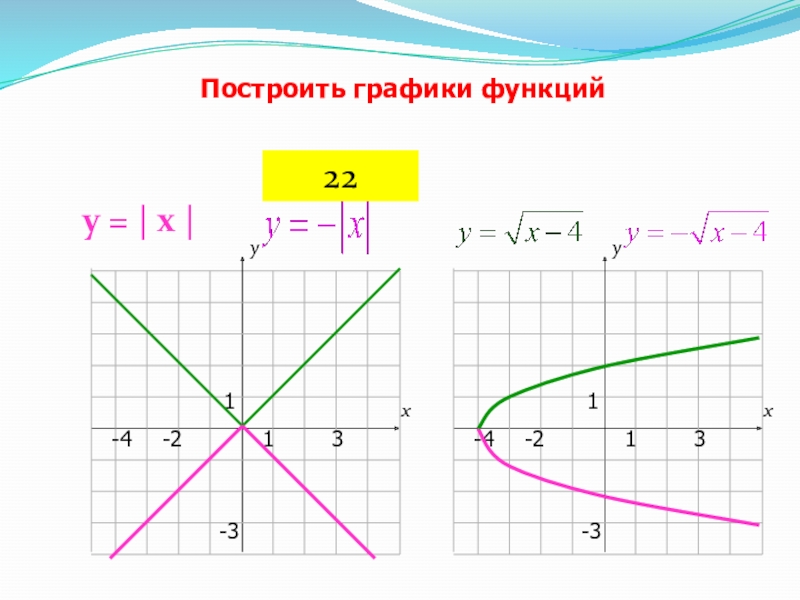
- 35. Построить графики функций22у = | х |
- 36. Изучение нового материала. Основные приёмы преобразования
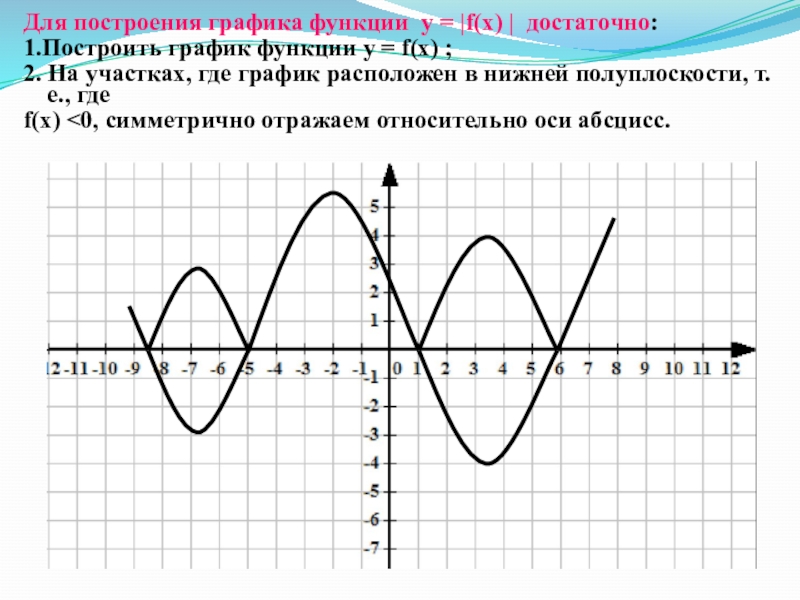
- 37. Для построения графика функции у = |f(х)
- 38. Для построения графика функции у = |f(х)
- 39. 7. Преобразованиеf(x) → │f(x)│ Часть графика, расположенная
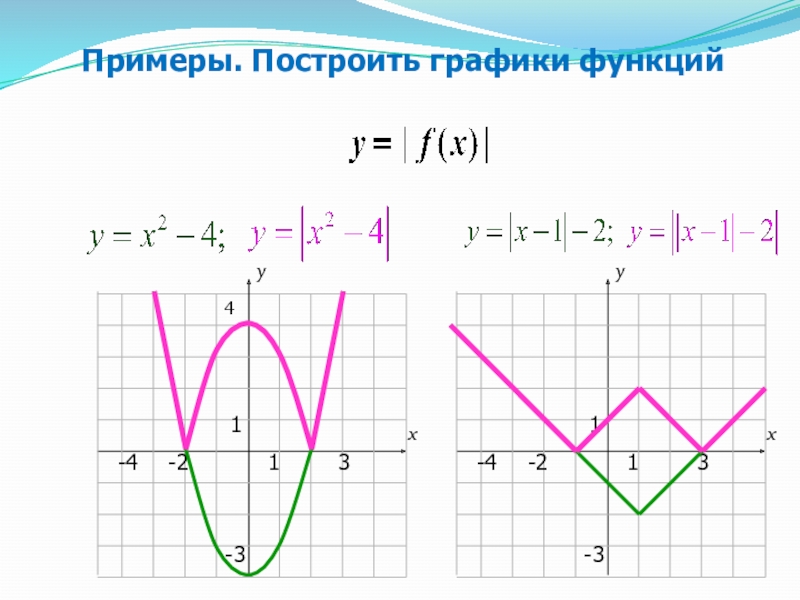
- 40. Примеры. Построить графики функций 4
- 41. График функции у
- 42. График функции у
- 43. f(x) → f(│x│)8. Преобразование Часть графика, расположенная
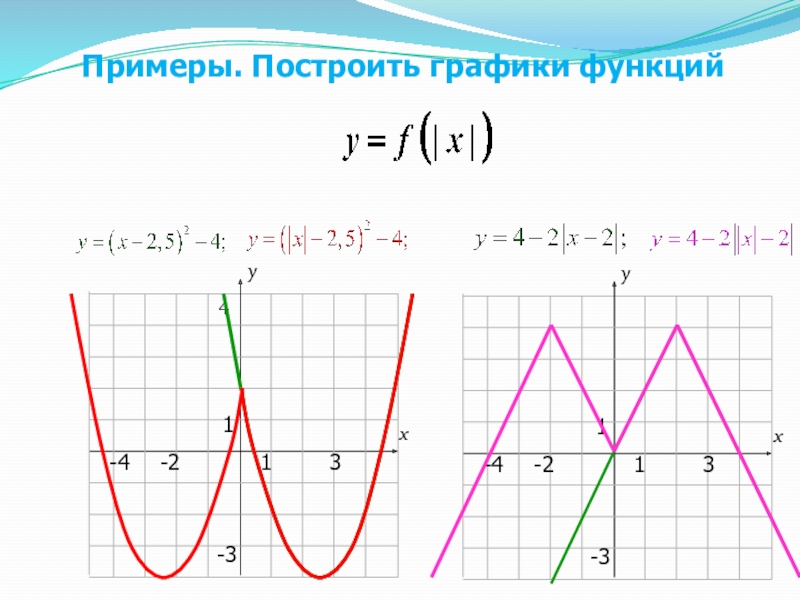
- 44. 4Примеры. Построить графики функций
- 45. Проверим результаты усвоения материала. Решение примеров.
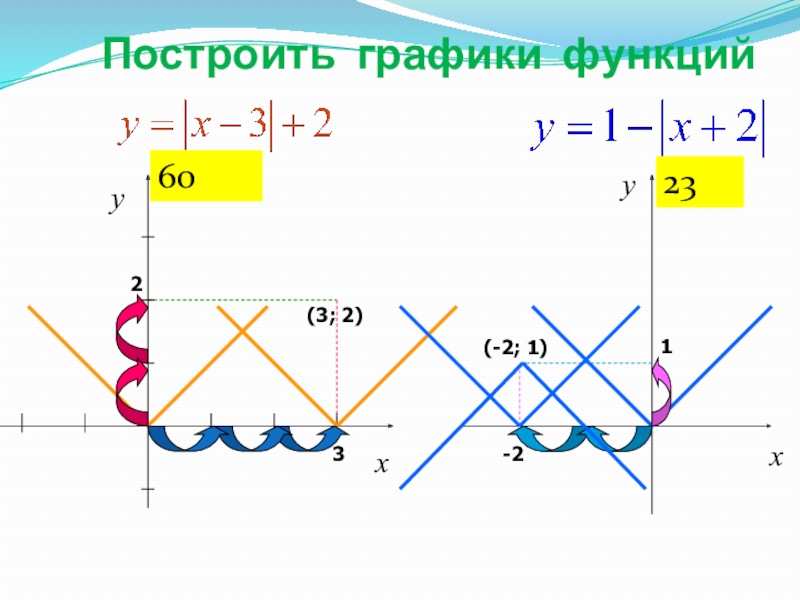
- 46. Построить графики функцийху32ху-21(3; 2)(-2; 1)6023
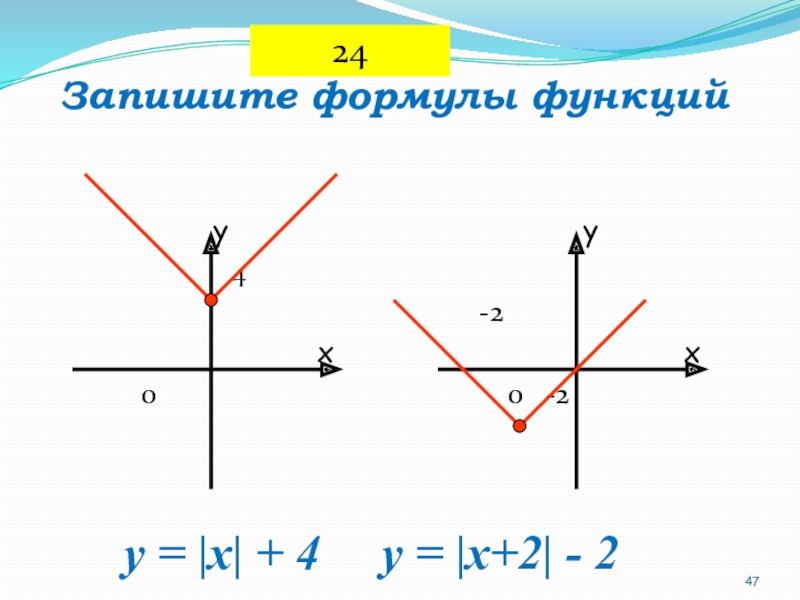
- 47. Запишите формулы функций y
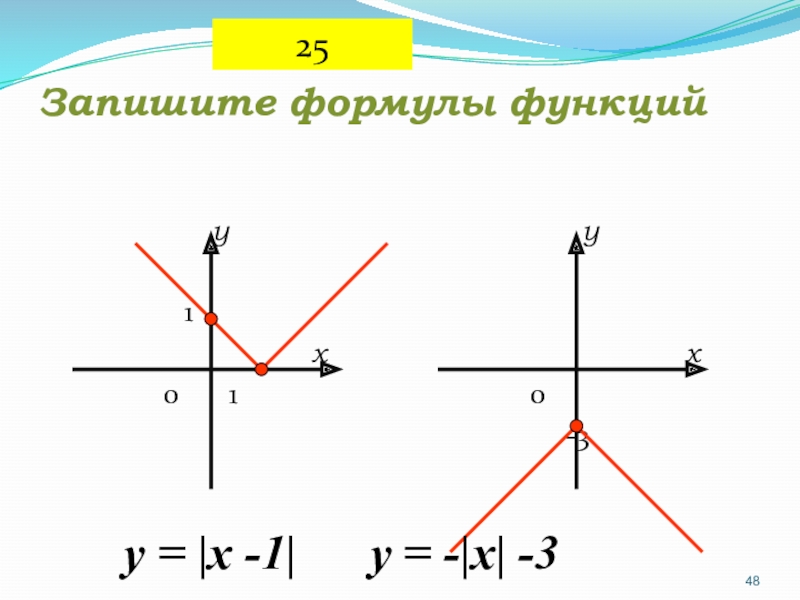
- 48. Запишите формулы функций y
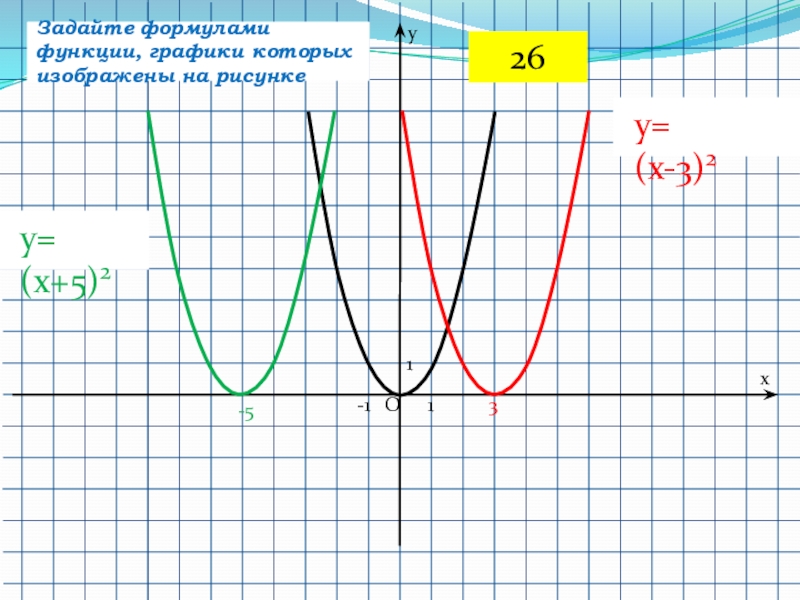
- 49. 1-11Oyx3y= (x-3)2Задайте формулами функции, графики которых изображены на рисунке -5y= (x+5)226
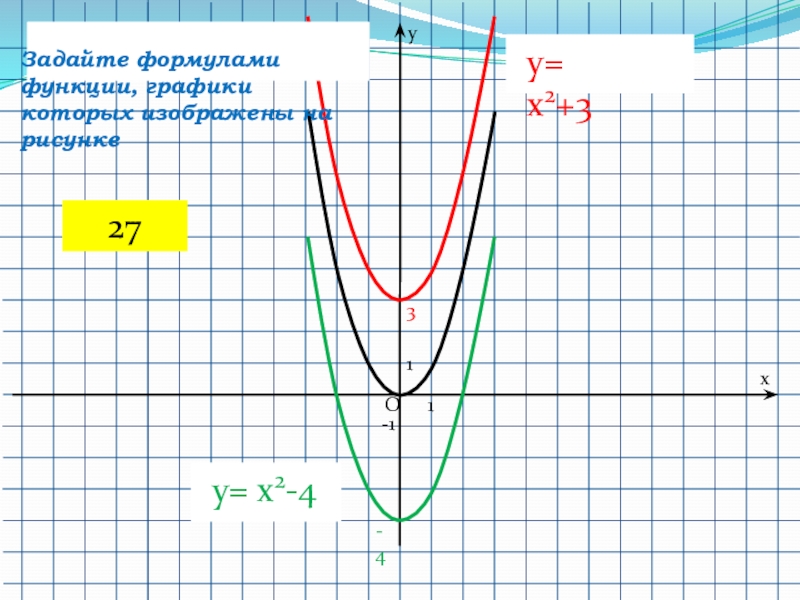
- 50. 1-11Oyx3y= x2+3Задайте формулами функции, графики которых изображены на рисунке -4y= x2-427
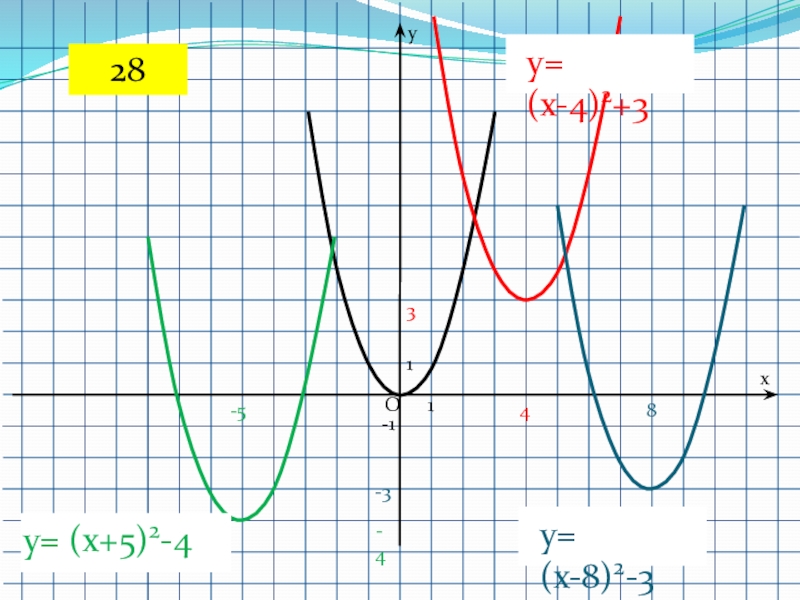
- 51. 1-11Oyx3y= (x-4)2+3-4y= (x+5)2-4y= (x-8)2-348-3-528
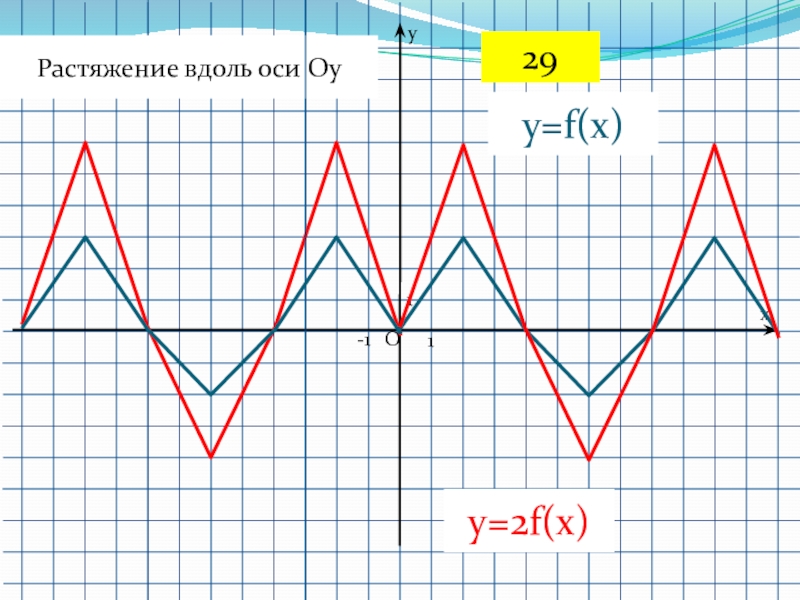
- 52. 1-11Oyxy=f(x)Растяжение вдоль оси Oy y=2f(x)29
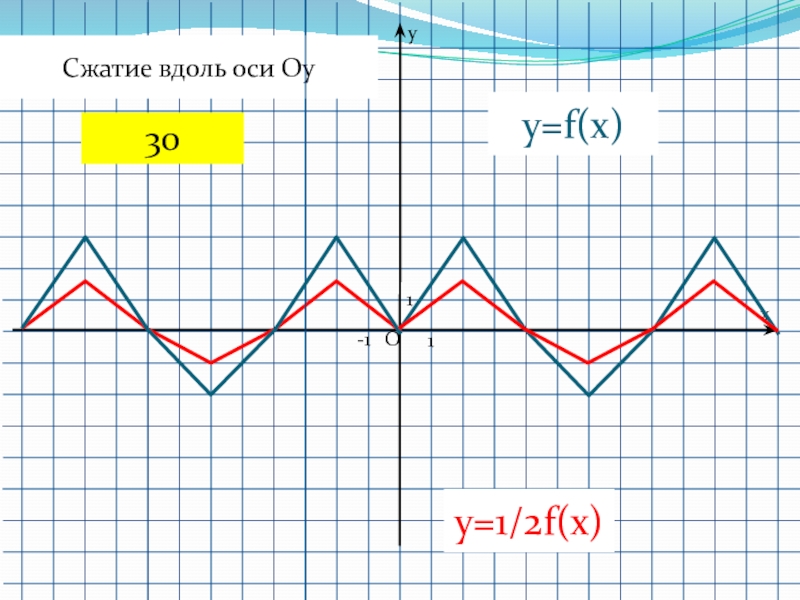
- 53. 1-11Oyxy=f(x)Сжатие вдоль оси Oy y=1/2f(x)30
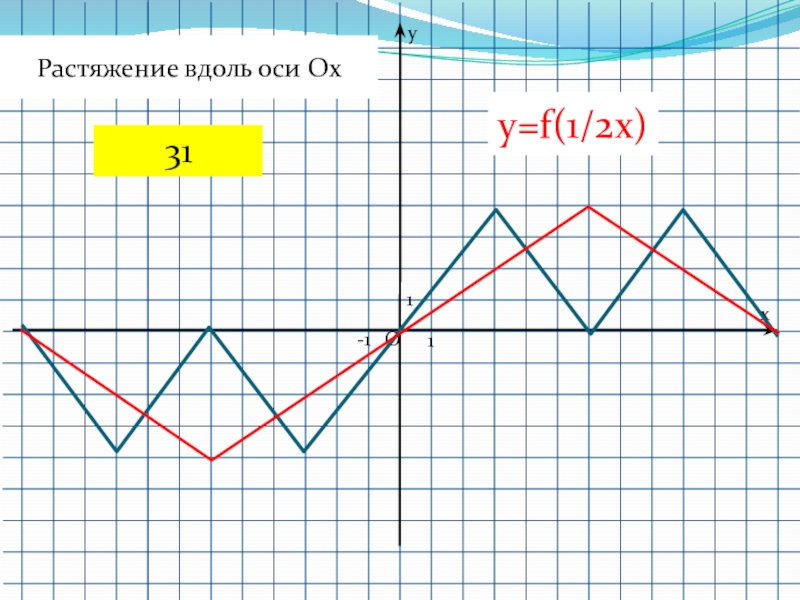
- 54. 1-11Oyxy=f(1/2x)Растяжение вдоль оси Ox 31
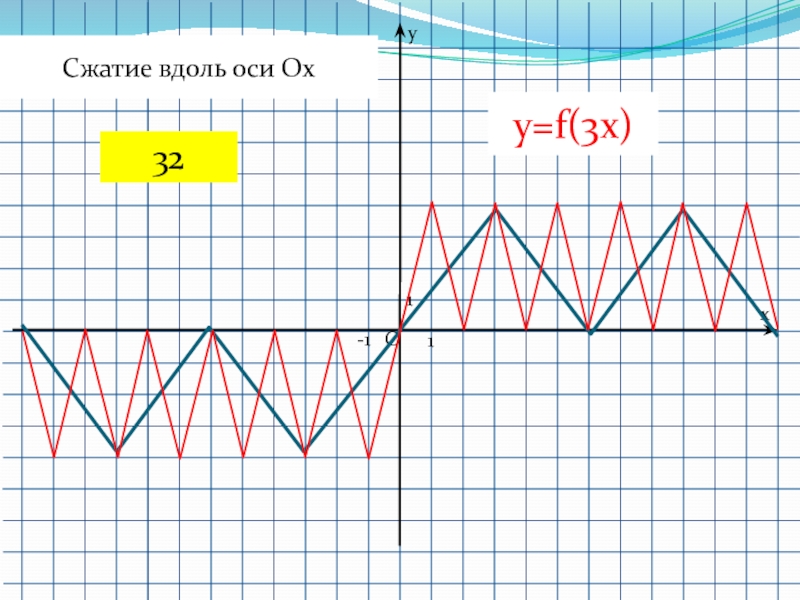
- 55. 1-11Oyxy=f(3x)Сжатие вдоль оси Ox 32
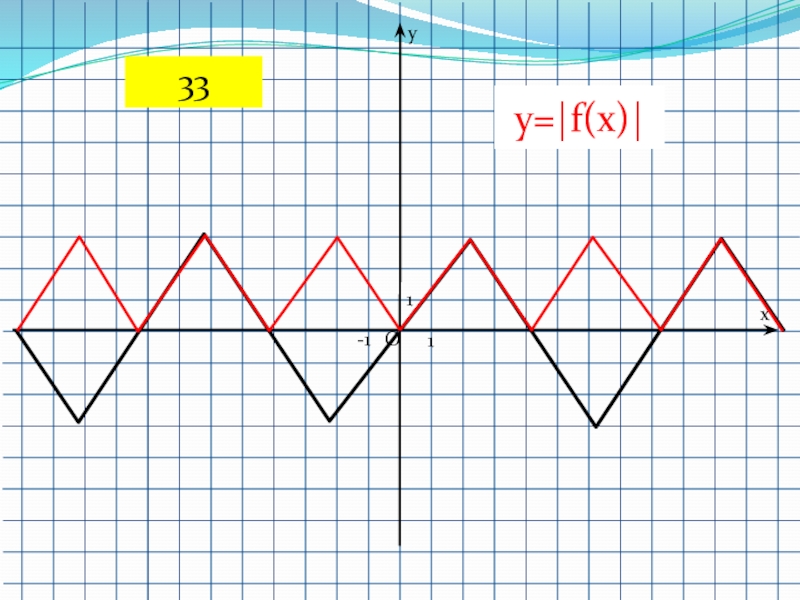
- 56. 1-11Oyxy=|f(x)|33
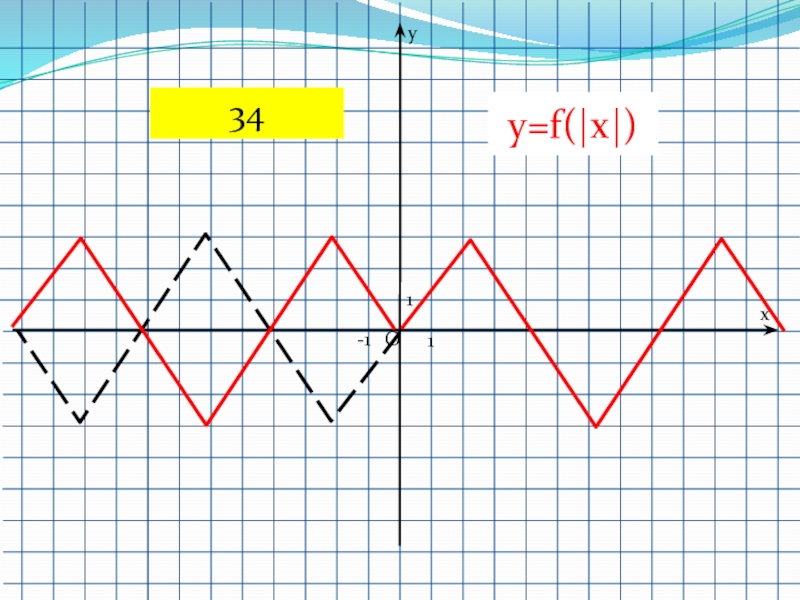
- 57. 1-11Oyxy=f(|x|)34
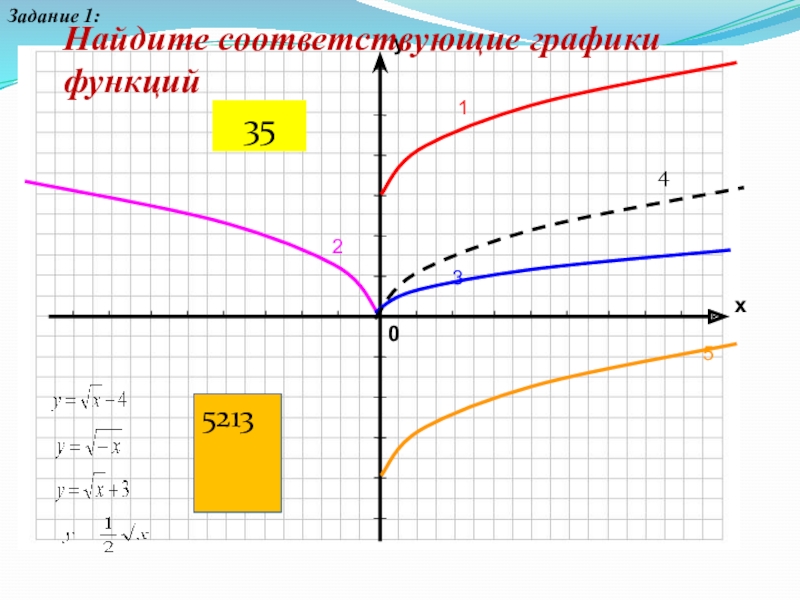
- 58. 12354Найдите соответствующие графики функцийЗадание 1: 521335
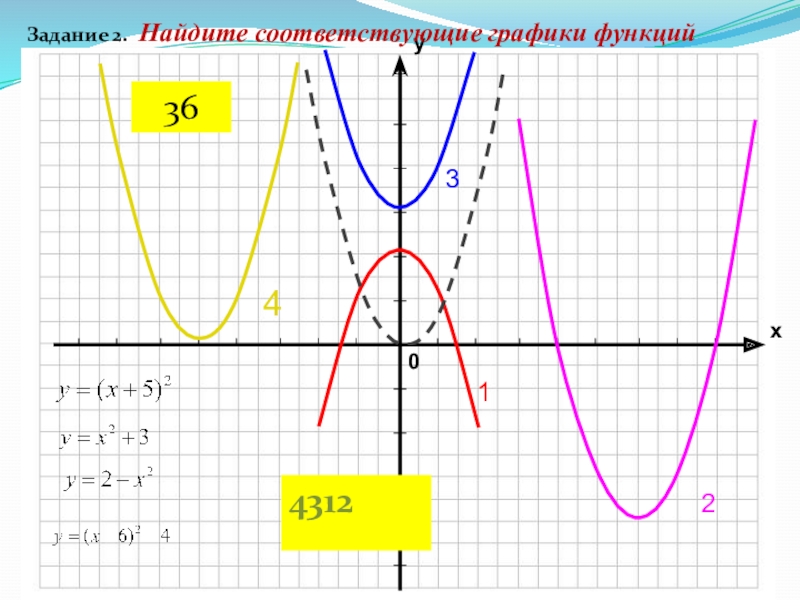
- 59. 4123 Найдите соответствующие графики функцийЗадание 2.431236
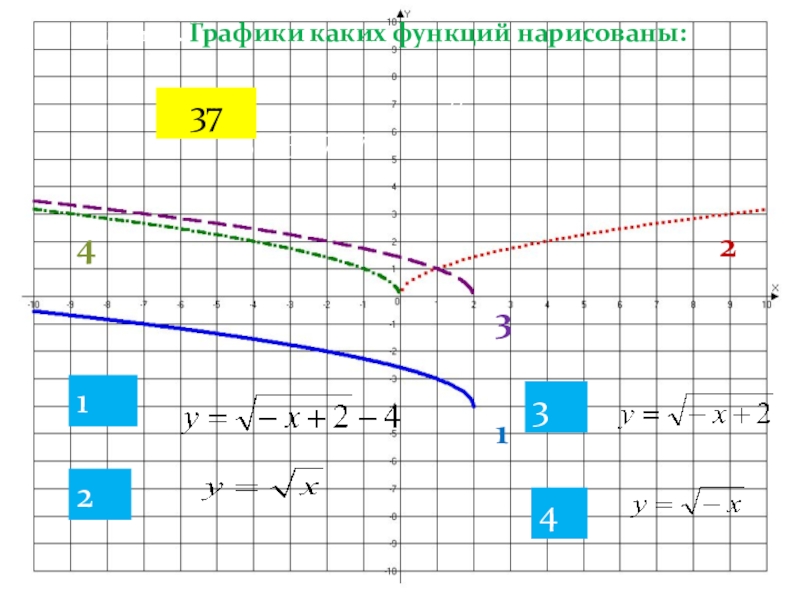
- 60. Задание 4. Графики каких функций нарисованы:12342431333337373337
- 61. Задания 23 ОГЭ. Желаю удачи
- 62. у1234-213Пример 3. Постройте график функции
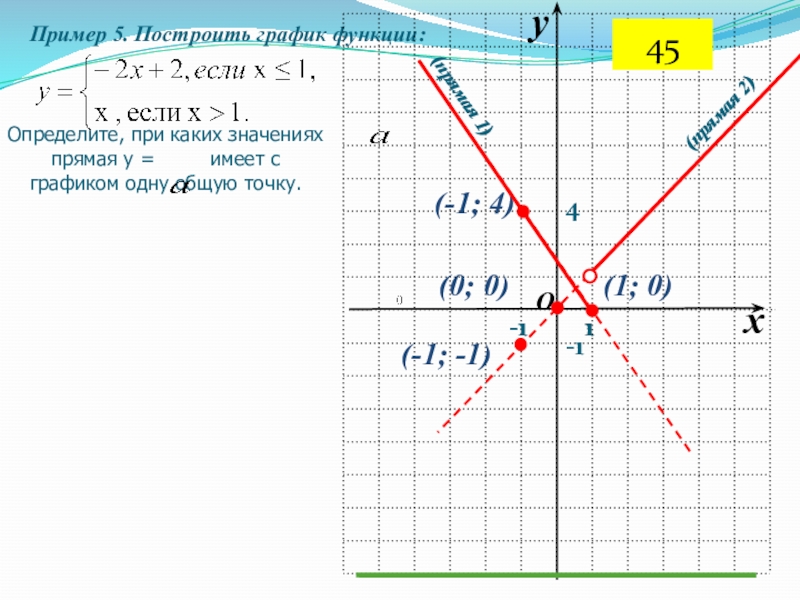
- 63. Пример 4. Построить график функцииОпределите, при каких
- 64. Построим в одной системе координат графики функций:хуРешить
- 65. Графический метод Решите графически неравенство 3) Находим
- 66. у=√х√х ≥ х-6Построим в одной системе координат
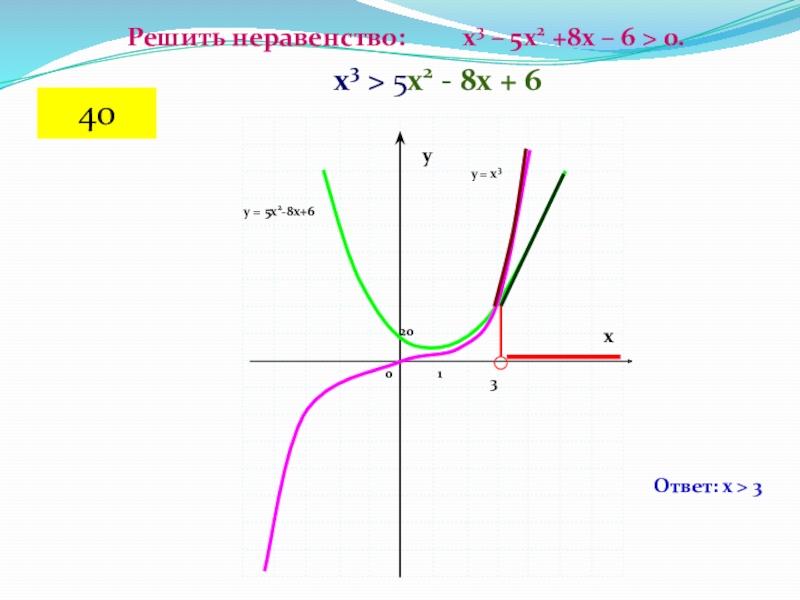
- 67. Решить неравенство: х3
- 68. -1-2-3-4-5-61 2 3 4
- 69. Пример 2. При каких значениях с прямая
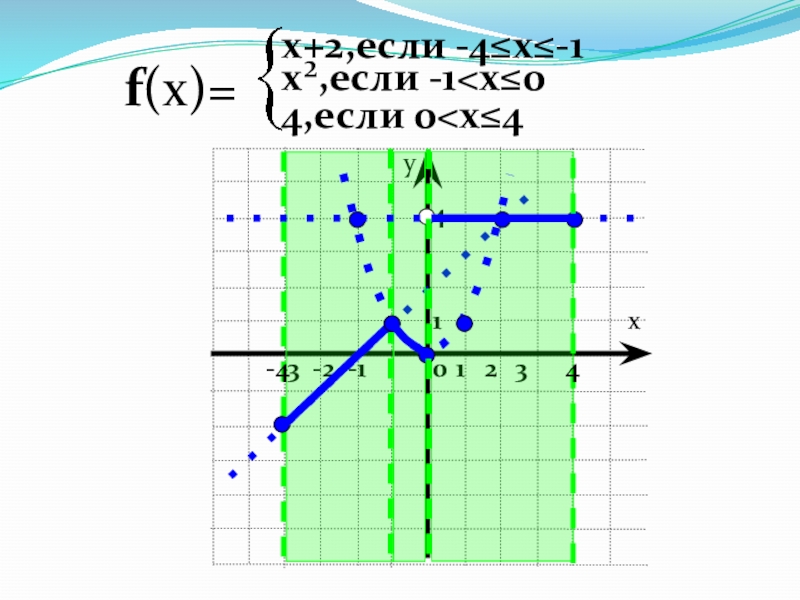
- 70. f(x)=х+2,если -4≤х≤-1х²,если -1
- 71. 1(1; 0) (-1; 4) (прямая 1)(-1; -1)
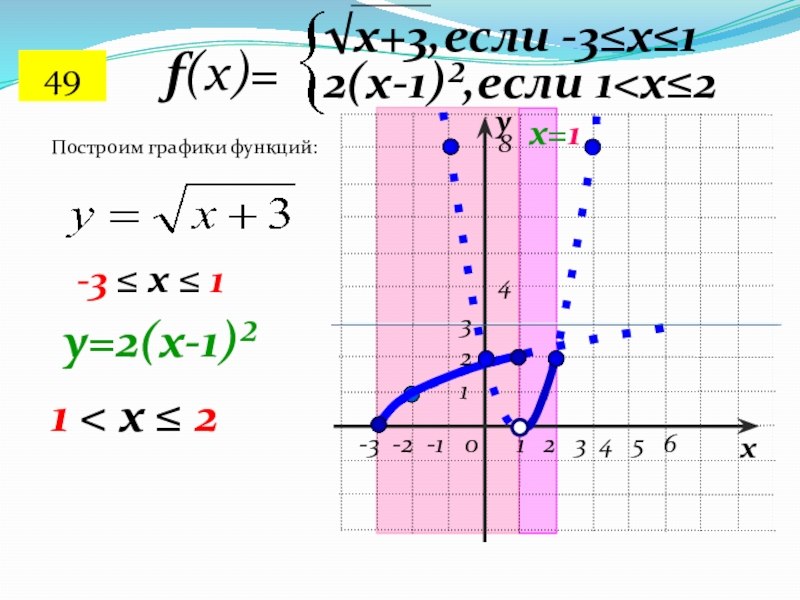
- 72. ухf(x)=√x+3,если -3≤х≤12(х-1)²,если 1
- 73. Графики функции широко используются в различных областях
- 74. Стремись к знаниям71
- 75. Понравился урок и тема понята:Понравился урок, но
- 76. Молодец!
- 77. Спасибо за урок!
- 78. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Функционально-графический подход к решению задач.
Кузьмина В Л
Моргаушская СОШ
В математике
есть своя красота, как в живописи и поэзии.
Слайд 2Цель:
Обобщить и закрепить умения строить графики функций с помощью их
преобразования.
Виды деятельности:
сопоставлять графики и их формулы, строить графики
функций, выполнять нужные вычисления, работать в парах.Слайд 31). Повторение. Графики элементарных функций.
Линейная функция
Квадратичная функция
Дробно-линейная функция
Степенная функция
Окружность
Функция
Желаю интересной работы на уроке.
Слайд 4k < 0
k > 0
b
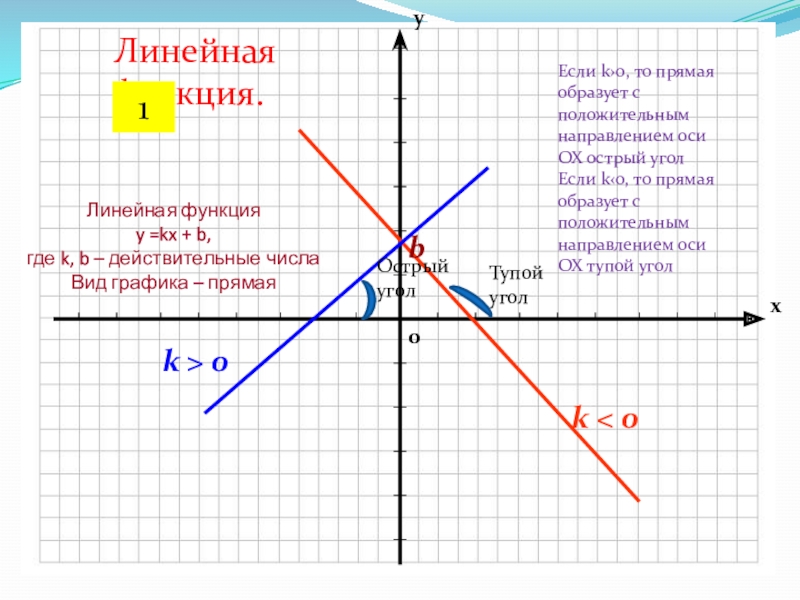
Линейная функция
y =kx + b,
где
k, b – действительные числа
Вид графика – прямая
Если k›0, то
прямая образует с положительным направлением оси ОХ острый уголЕсли k‹0, то прямая образует с положительным направлением оси ОХ тупой угол
Линейная функция.
Острый угол
Тупой угол
1
Слайд 5b
b > 0
b
b < 0
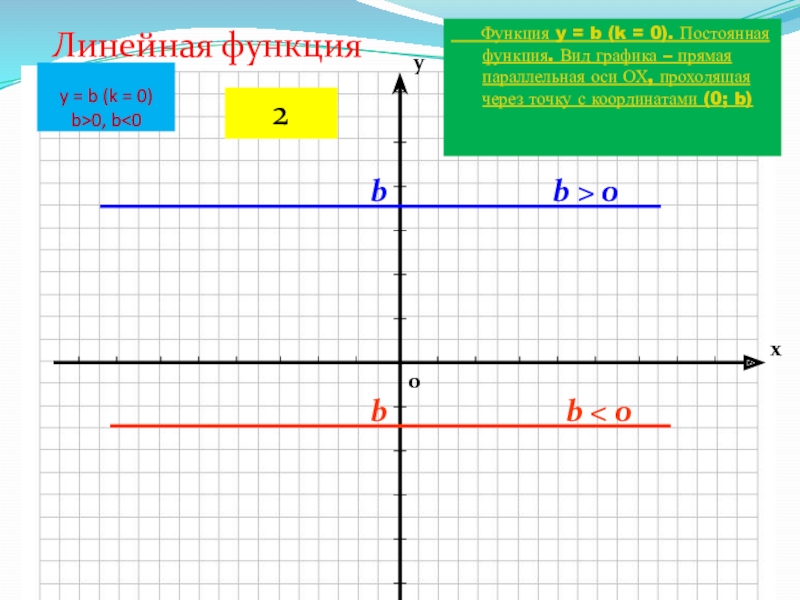
y = b (k = 0)
b>0,
b
Постоянная функция. Вид графика – прямая параллельная оси ОХ, проходящая через точку с координатами (0; b)Линейная функция
2
Слайд 6k < 0
k > 0
k
k
1
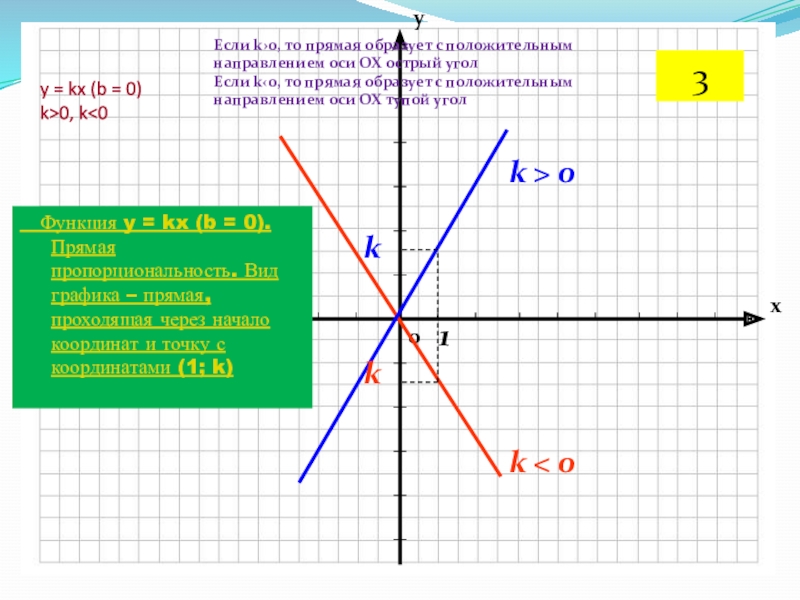
y = kx (b = 0)
k>0,
k
пропорциональность. Вид графика – прямая, проходящая через начало координат и точку с координатами (1; k)Если k›0, то прямая образует с положительным направлением оси ОХ острый угол
Если k‹0, то прямая образует с положительным направлением оси ОХ тупой угол
3
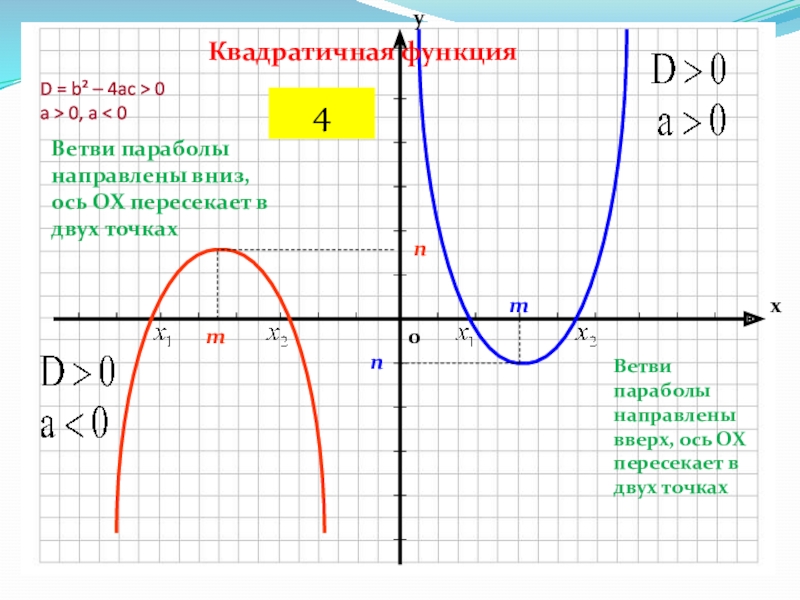
Слайд 7D = b² – 4ac > 0 a > 0, a
< 0
Ветви параболы направлены вверх, ось ОХ пересекает в двух
точкахКвадратичная функция
Ветви параболы направлены вниз, ось ОХ пересекает в двух точках
4
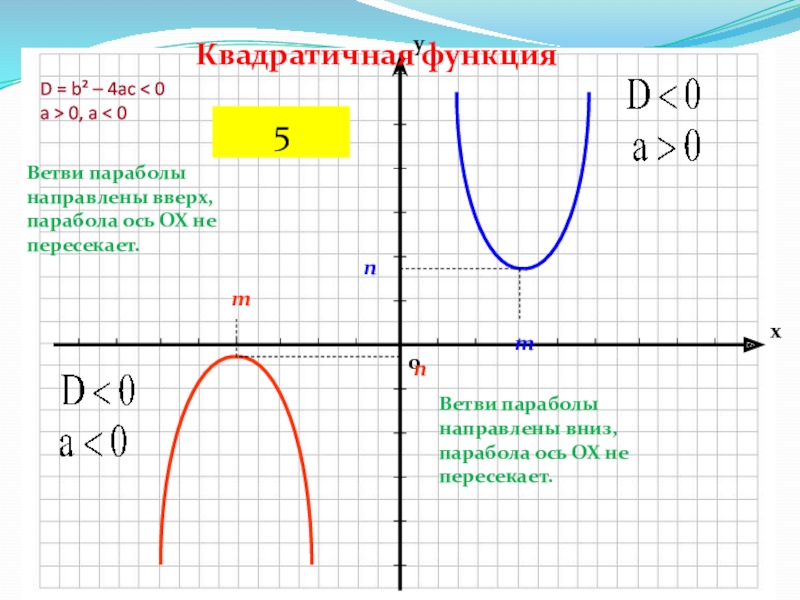
Слайд 8D = b² – 4ac < 0 a > 0, a
< 0
Ветви параболы направлены вверх, парабола ось ОХ не пересекает.
Ветви
параболы направлены вниз, парабола ось ОХ не пересекает.Квадратичная функция
5
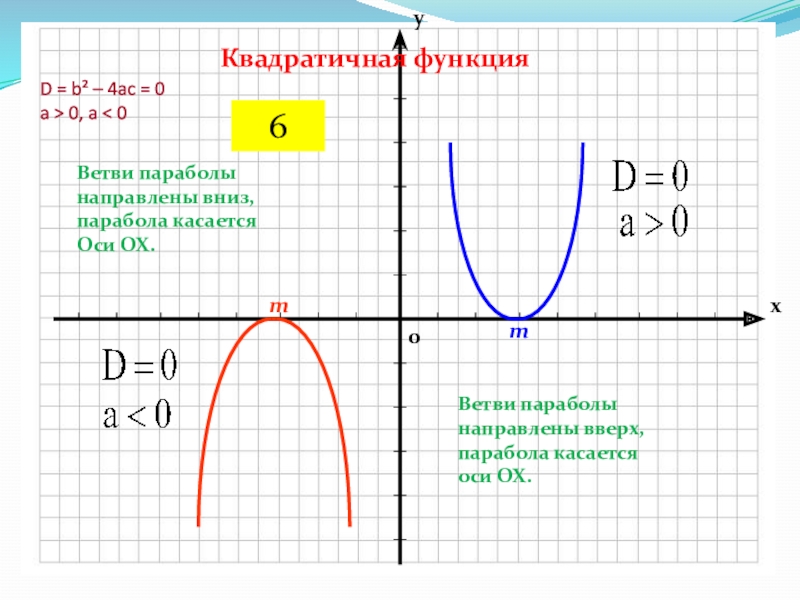
Слайд 9D = b² – 4ac = 0 a > 0, a
< 0
Ветви параболы направлены вниз, парабола касается Оси ОХ.
Ветви параболы
направлены вверх, парабола касается оси ОХ.Квадратичная функция
6
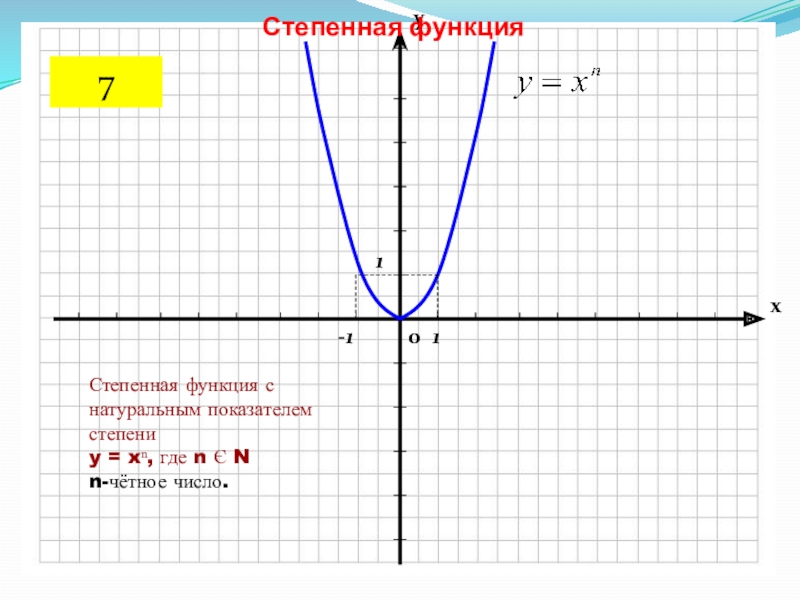
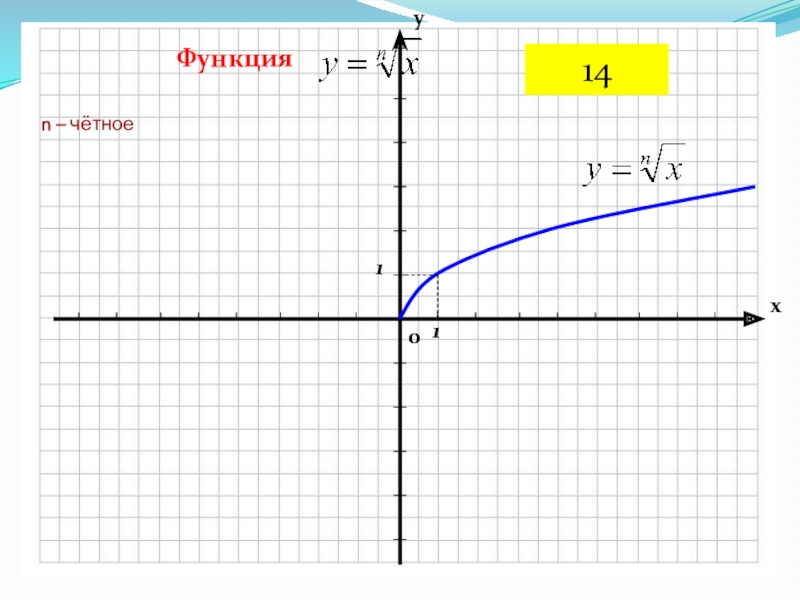
Слайд 10Степенная функция
Степенная функция с натуральным показателем степени
y = xⁿ, где
n Є N
n-чётное число.
7
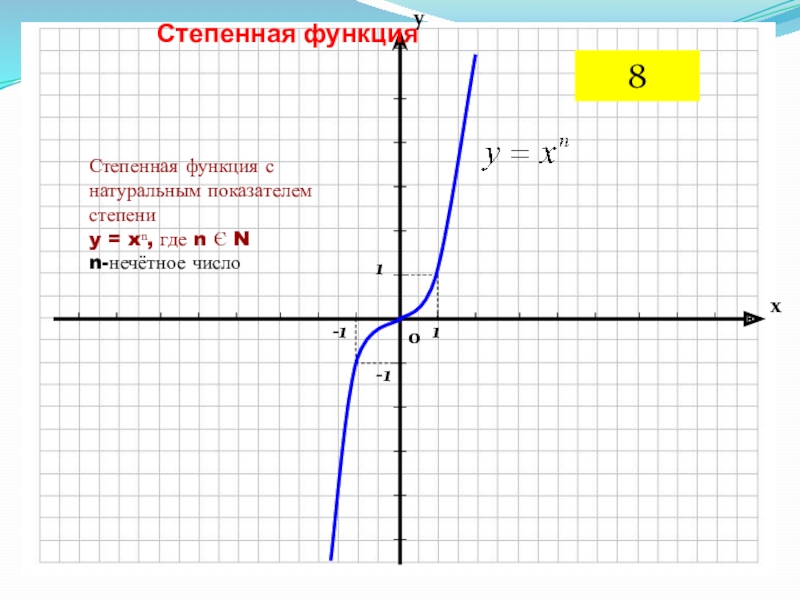
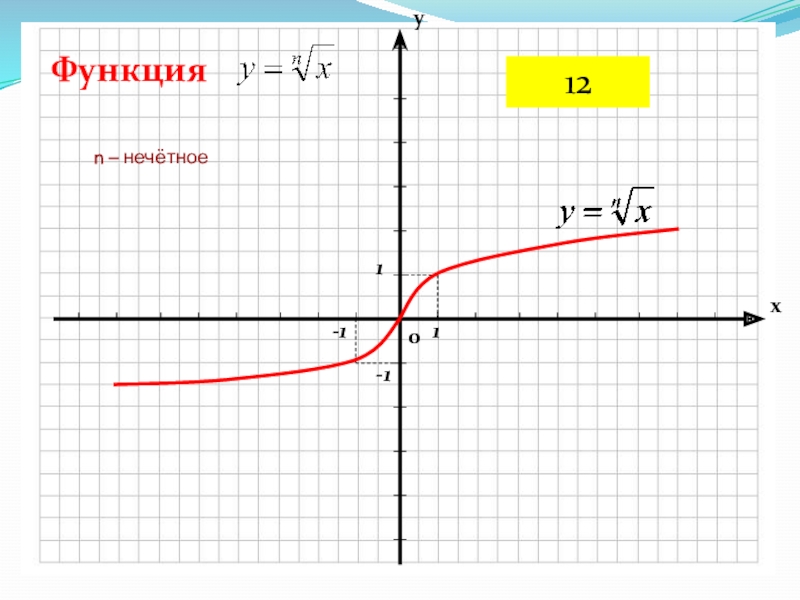
Слайд 11Степенная функция
Степенная функция с натуральным показателем степени
y = xⁿ, где
n Є N
n-нечётное число
8
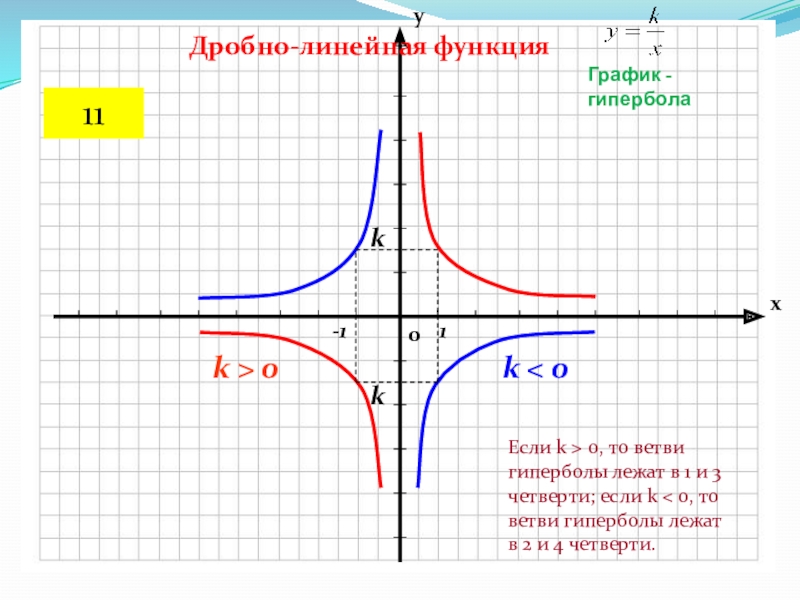
Слайд 14k > 0
k < 0
График - гипербола
Дробно-линейная функция
Если k >
0, то ветви гиперболы лежат в 1 и 3 четверти;
если k < 0, то ветви гиперболы лежат в 2 и 4 четверти.11
Слайд 17Уравнение окружности.
(х – а)2 + (у – b)2 = R2
уравнение
окружности, где
А(а;b) − центр, R − радиус,
х и у –
координаты точки окружности. 15
Слайд 19
«…Математика … выявляет порядок, симметрию и определенность, а это
– важнейшие виды прекрасного»
Аристотель
Слайд 202).Повторение пройденного материала.
Основные приёмы преобразования графиков.
Параллельный перенос вдоль оси абсцисс
Параллельный
перенос вдоль оси ординат
Растяжение и сжатие вдоль оси абсцисс
Растяжение и
сжатие вдоль оси ординатПреобразование симметрии относительно оси абсцисс
Преобразование симметрии относительно оси ординат
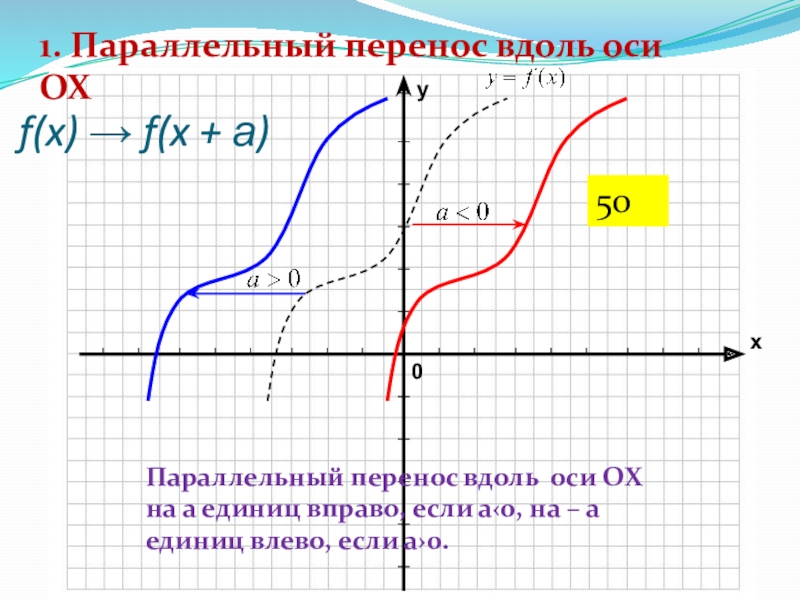
Слайд 21f(x) → f(x + а)
1. Параллельный перенос вдоль оси
OX
Параллельный перенос вдоль оси OХ на а единиц вправо, если
а‹0, на – а единиц влево, если а›0.50
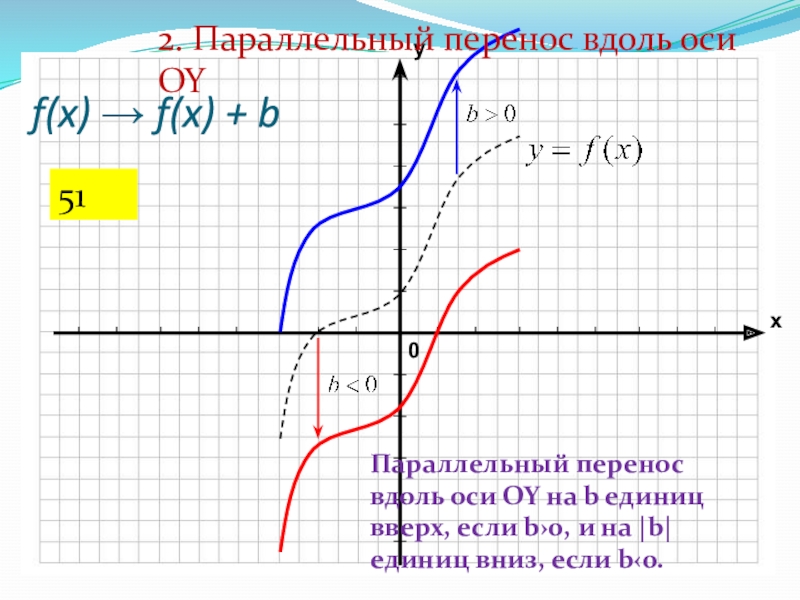
Слайд 22f(x) → f(x) + b
2. Параллельный перенос вдоль оси
OY
Параллельный перенос вдоль оси OY на b единиц вверх, если
b›0, и на |b| единиц вниз, если b‹0.51
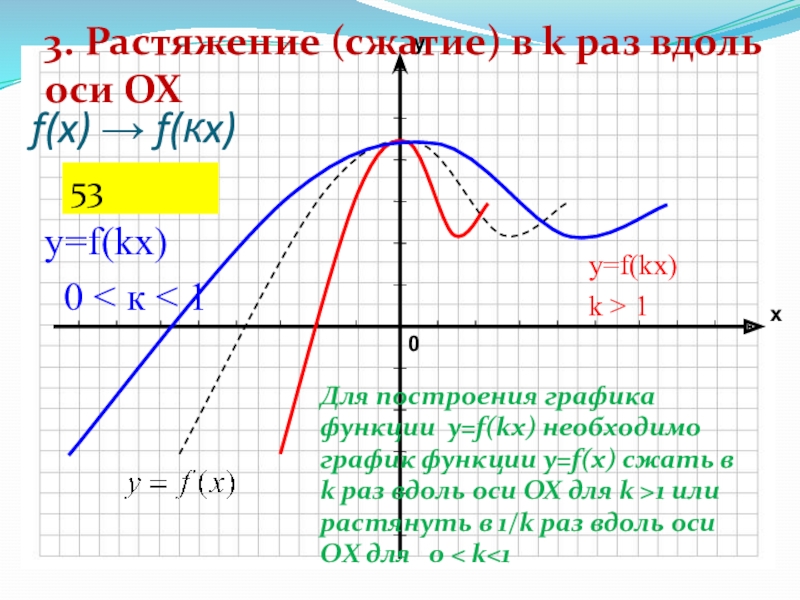
Слайд 26f(x) → f(кx)
y=f(kx)
k > 1
3. Растяжение (сжатие) в k
раз вдоль оси OX
0 < к < 1
y=f(kx)
Для построения графика
функции y=f(kx) необходимо график функции y=f(x) сжать в k раз вдоль оси ОХ для k >1 или растянуть в 1/k раз вдоль оси OХ для 0 < k<153
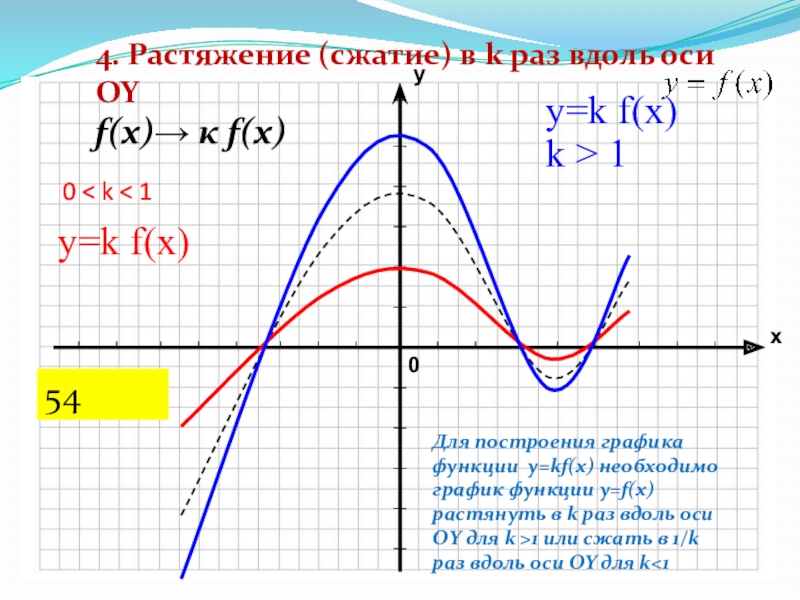
Слайд 270 < k < 1
4. Растяжение (сжатие) в k раз
вдоль оси OY
f(x)→ к f(x)
y=k f(x)
k > 1
y=k
f(x)Для построения графика функции y=kf(x) необходимо график функции y=f(x) растянуть в k раз вдоль оси ОY для k >1 или сжать в 1/k раз вдоль оси OY для k<1
54
Слайд 36Изучение нового материала.
Основные приёмы преобразования графиков.
7. Построение графика функции
у =│f(x)│
8. Построение графика функции у = f(│x│)
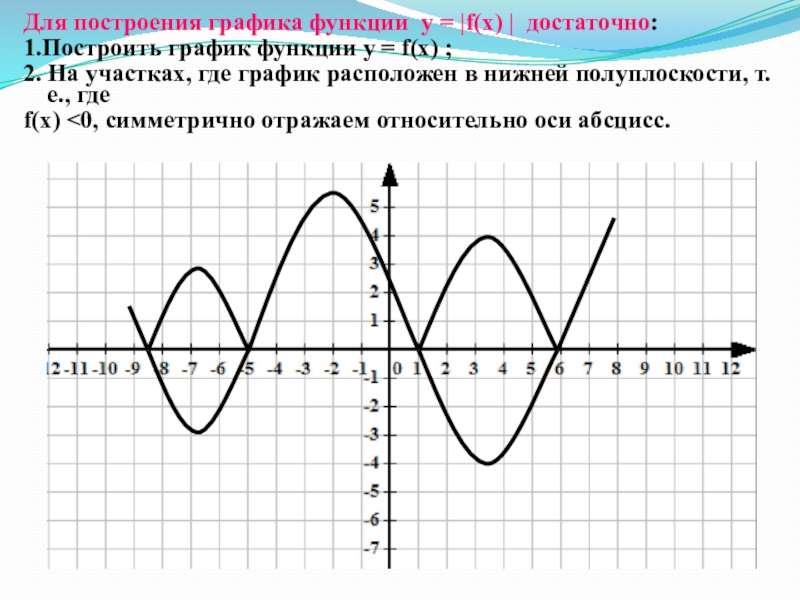
Слайд 37Для построения графика функции у = |f(х) | достаточно:
1.Построить график
функции у = f(х) ;
2. На участках, где график расположен
в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс.
Слайд 38Для построения графика функции у = |f(х) | достаточно:
1.Построить график
функции у = f(х) ;
2. На участках, где график расположен
в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс.
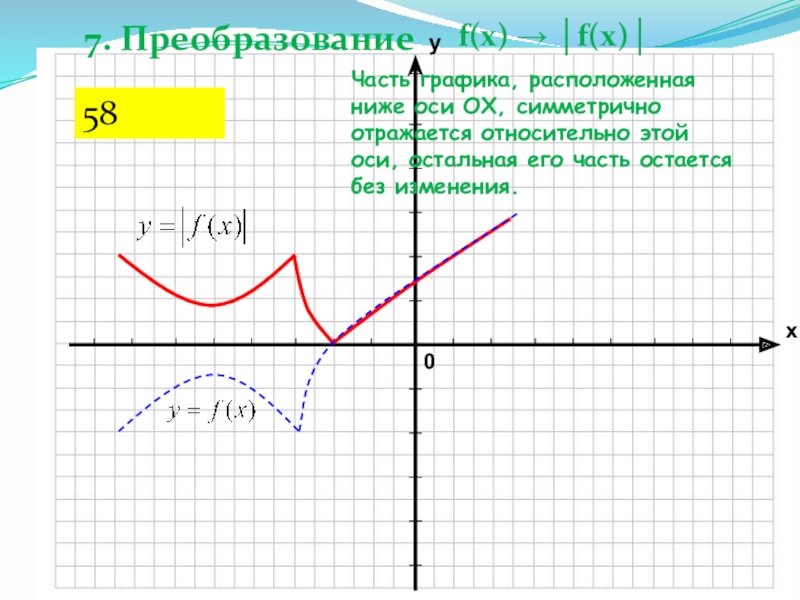
Слайд 397. Преобразование
f(x) → │f(x)│
Часть графика, расположенная ниже оси
OX, симметрично отражается относительно этой оси, остальная его часть остается
без изменения.58
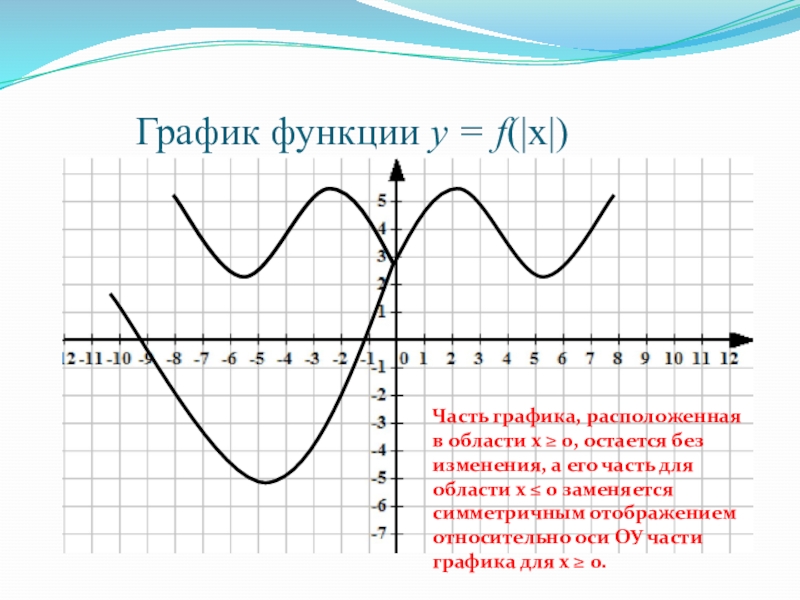
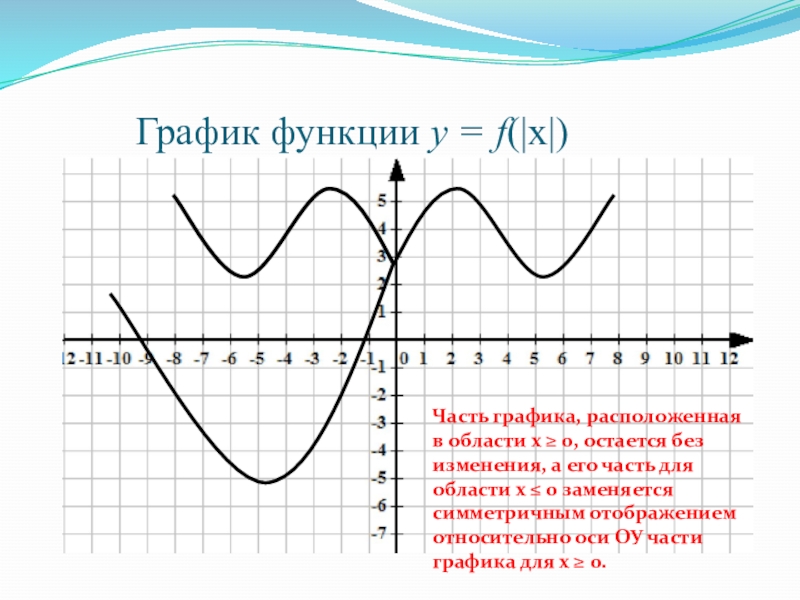
Слайд 41 График функции у = f(|х|)
Часть графика,
расположенная в области х ≥ 0, остается без изменения, а
его часть для области х ≤ 0 заменяется симметричным отображением относительно оси ОУ части графика для х ≥ 0.Слайд 42 График функции у = f(|х|)
Часть графика,
расположенная в области х ≥ 0, остается без изменения, а
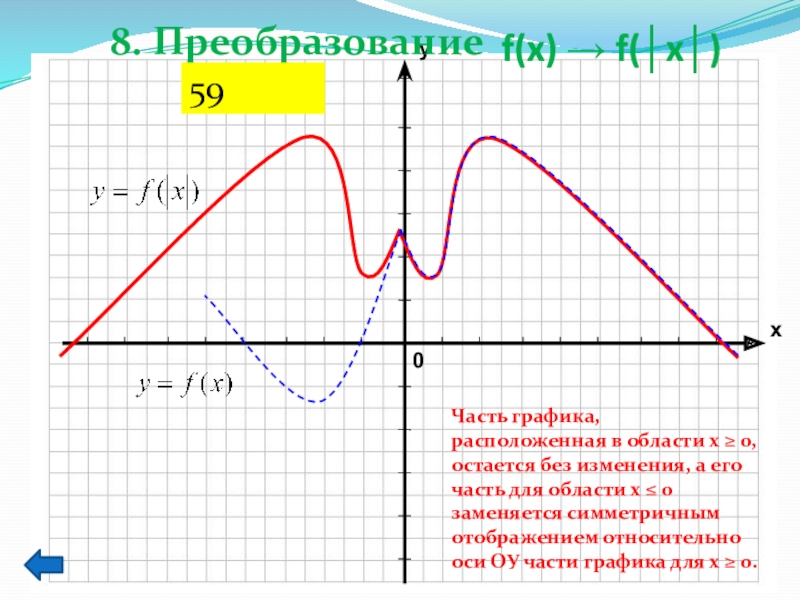
его часть для области х ≤ 0 заменяется симметричным отображением относительно оси ОУ части графика для х ≥ 0.Слайд 43f(x) → f(│x│)
8. Преобразование
Часть графика, расположенная в области х
≥ 0, остается без изменения, а его часть для области
х ≤ 0 заменяется симметричным отображением относительно оси ОУ части графика для х ≥ 0.59
Слайд 491
-1
1
O
y
x
3
y= (x-3)2
Задайте формулами функции, графики которых изображены на рисунке
-5
y=
(x+5)2
26
Слайд 62 у
1
2
3
4
-2
1
3
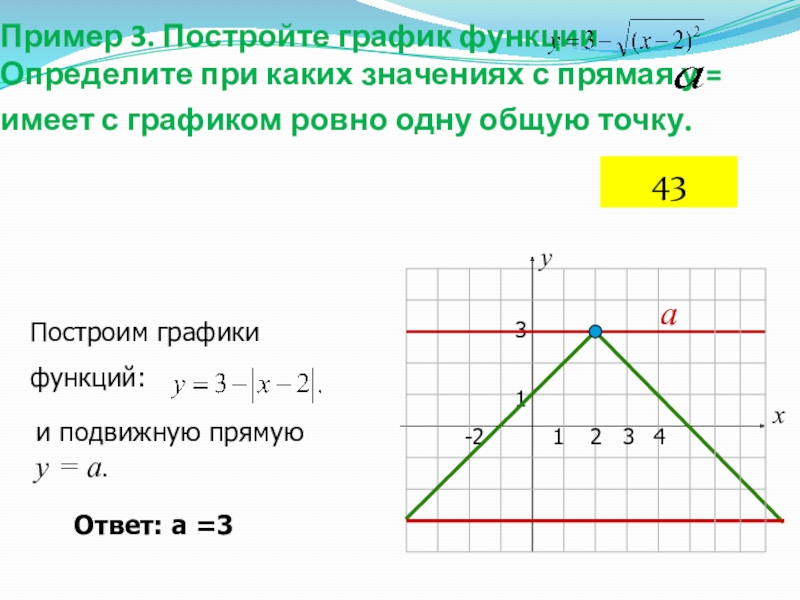
Пример 3. Постройте график функции
Определите при каких значениях
с прямая у = имеет с графиком ровно одну общую
точку.х
Построим графики
функций:
Ответ: а =3
и подвижную прямую у = а.
а
43
Слайд 63
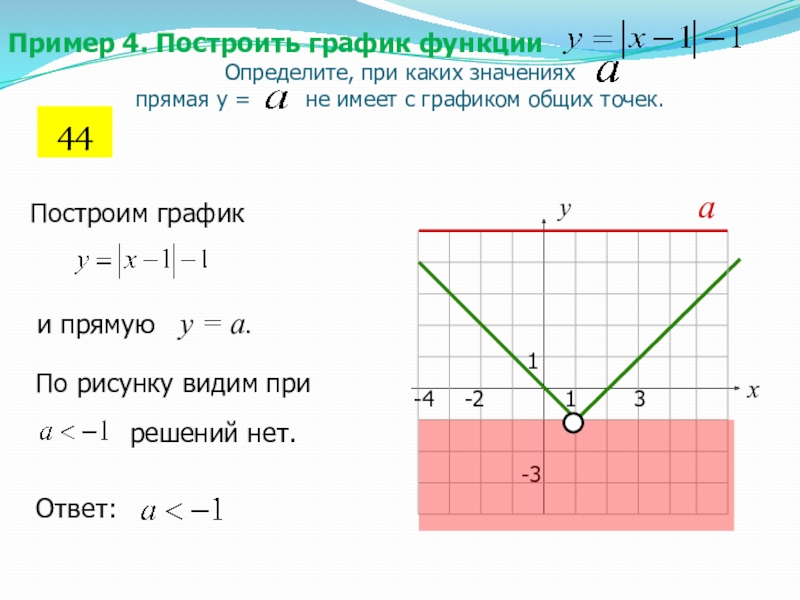
Пример 4. Построить график функции
Определите, при каких значениях
прямая у =
не имеет с графиком общих точек.
х
у
1
3
-4
1
-3
-2
Построим график
По рисунку видим при
и прямую у = а.
решений нет.
Ответ:
44
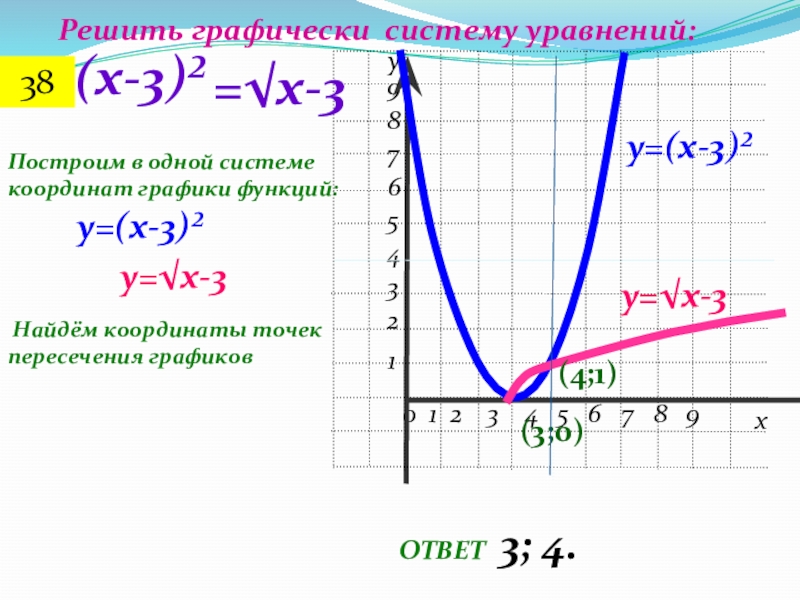
Слайд 64Построим в одной системе координат графики функций:
х
у
Решить графически систему уравнений:
(х-3)²
у=(х-3)²
у=(х-3)²
у=√х-3
Найдём координаты точек пересечения графиков
ОТВЕТ
3; 4.
(3;0)
=√х-3
(4;1)
у=√х-3
38
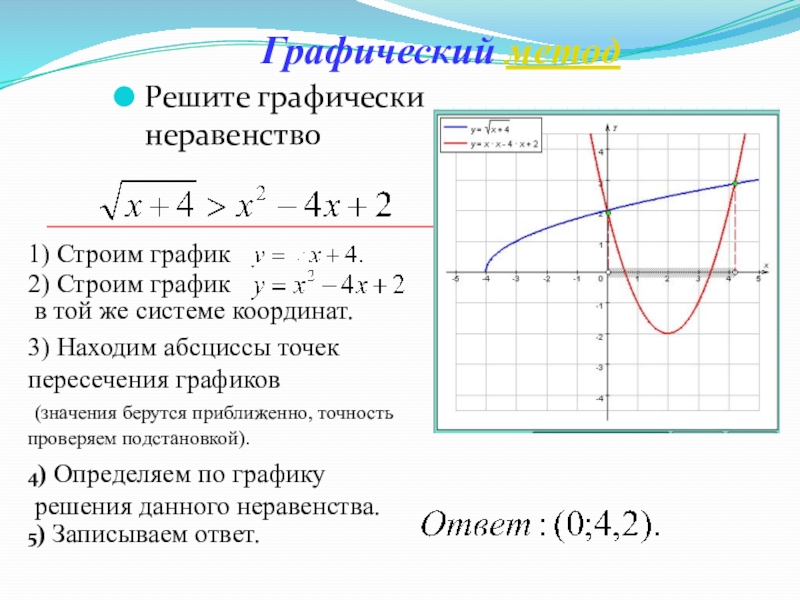
Слайд 65Графический метод
Решите графически неравенство
3) Находим абсциссы точек
пересечения графиков
(значения берутся приближенно, точность проверяем подстановкой).
4) Определяем по графику
решения
данного неравенства.5) Записываем ответ.
Слайд 66у=√х
√х ≥ х-6
Построим в одной системе координат графики функций:
у=х-6
Найдём абсциссы точек пересечения графиков
ОТВЕТ:
Х = [0;9]
Решить графически неравенство:
у=х-6
39
Слайд 68-1
-2
-3
-4
-5
-6
1 2 3 4 5
6 7
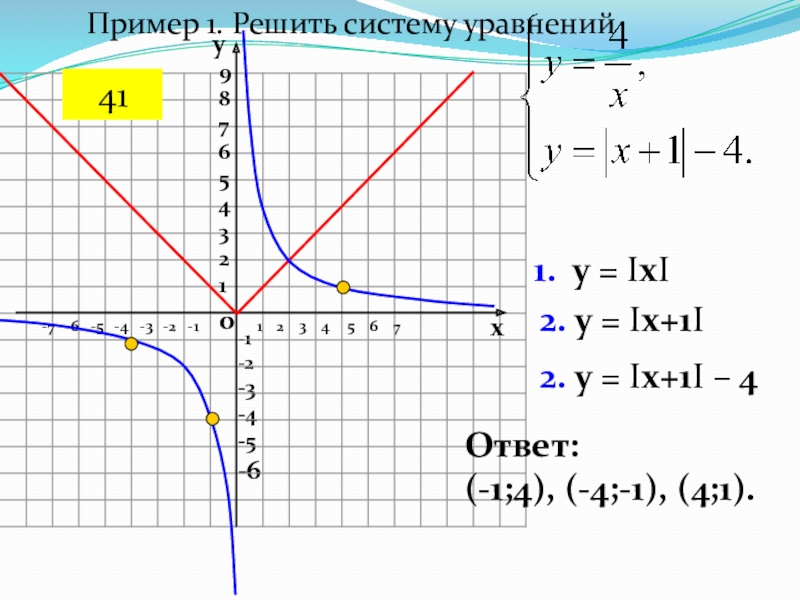
1. у = IхI
2. у =
Iх+1IОтвет:
(-1;4), (-4;-1), (4;1).
о
-7 -6 -5 -4 -3 -2 -1
9
8
7
6
5
4
3
2
1
у
х
2. у = Iх+1I – 4
Пример 1. Решить систему уравнений
41
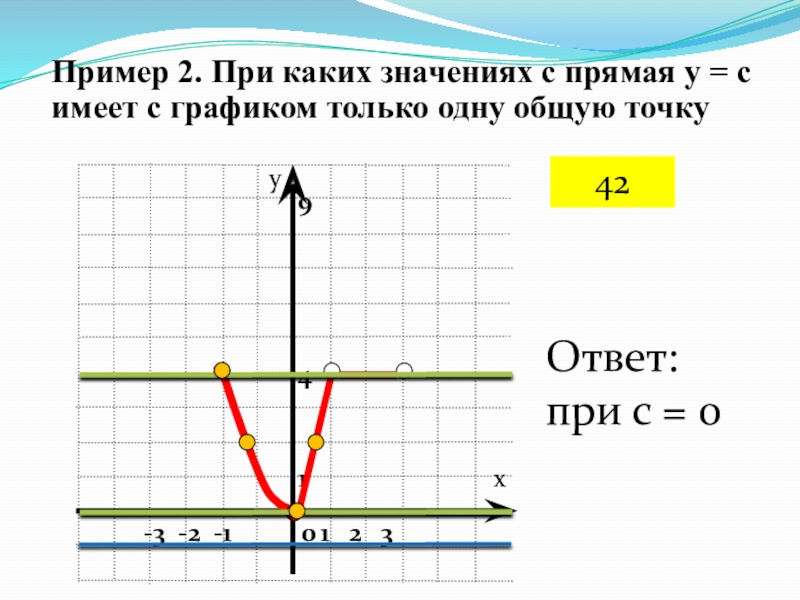
Слайд 69Пример 2. При каких значениях с прямая у = с
имеет с графиком только одну общую точку
Ответ:
при с = 0
42
Слайд 711
(1; 0)
(-1; 4)
(прямая 1)
(-1; -1)
(0; 0)
(прямая
2)
Определите, при каких значениях
прямая у =
имеет с графиком одну общую точку.45
Слайд 73Графики функции широко используются в различных областях науки, поэтому умение
строить, «читать», прогнозировать их «поведение» имеет огромную роль в практической
деятельности в инженерной области, гидрометеорологов и людей других математических специальностей.«Весь смысл жизни заключается в бесконечном завоевании неизвестного, в вечном усилии познать больше» Эмиль Золя









![Функционально-графический подход к решению задач. у=√х√х ≥ х-6Построим в одной системе координат графики функций:у=х-6 Найдём абсциссы у=√х√х ≥ х-6Построим в одной системе координат графики функций:у=х-6 Найдём абсциссы точек пересечения графиков ОТВЕТ:Х = [0;9]Решить](/img/thumbs/cb647da48f3c7fbb3d17ab488cc05403-800x.jpg)