Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрические преобразования в пространстве
Содержание
- 1. Геометрические преобразования в пространстве
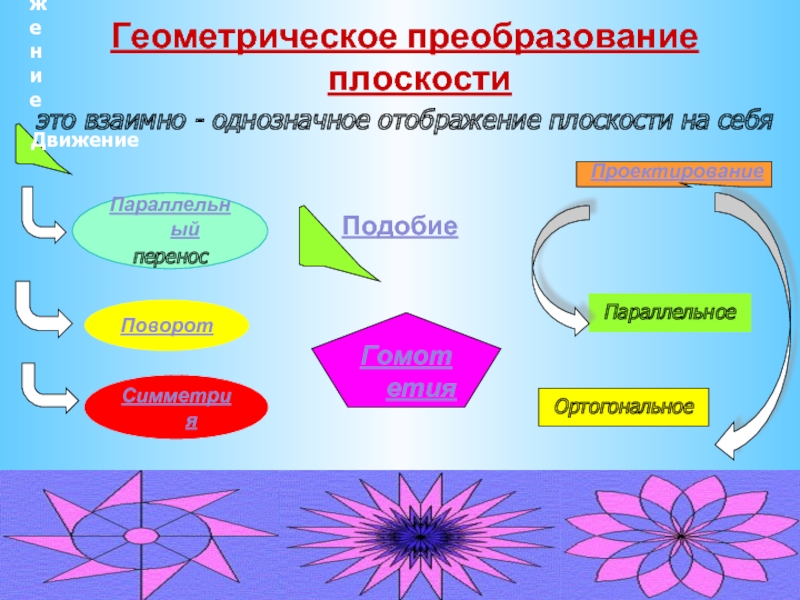
- 2. ДвижениеДвижениеПодобиеПараллельный переносПоворотСимметрияГомотетияПараллельноеОртогональноеГеометрическое преобразование плоскости это взаимно - однозначное отображение плоскости на себяПроектирование
- 3. хуzомм'••Точка М(х;у;z) переходит в точку М(х+а;у+b;z+c), где
- 4. Параллельный переносхуzоПараллельный перенос есть движениеДвижение, сохраняющее направление,является параллельным переносом
- 5. Поворотом плоскости около данной точки называется такое
- 6. Поворот в пространстве Спутники вращаются вокруг
- 7. Вращение галактик в космосе
- 8. «Симметрия является той идеей, посредством которой
- 9. к1к1•• КА1А••Отображение пространства на себя, при котором
- 10. Применение центральной симметрии
- 11. Центральная симметрия в природекактусы
- 12. Осевой симметрией с осьюℓ называется такое отображение
- 13. Осевая симметрия в архитектуреБиблиотека им. Лермонтова г. Ставрополь
- 14. Осевая симметрия храмовЦерковь во имя апостола Андрея Первозванного г. Ставрополь.Церковь Андрея Первозванного.г. Ставрополь
- 15. ОсеваясимметрияОсеваясимметрияживотногомира
- 16. Осевая симметрияв природе
- 17. ввтехникеОсевая симметрия
- 18. Осевая симметрия в литературеАЖЭОсевая симметрия в буквахА,
- 19. Зеркальной симметрией(симметрией относительно плоскости) называется такое отображение
- 20. З е р к а л ь
- 21. Преобразование фигуры F в фигуру F‘ называется
- 22. Гомотетией с центром О и коэффициентом k≠0
- 23. Киновкинотеатрах
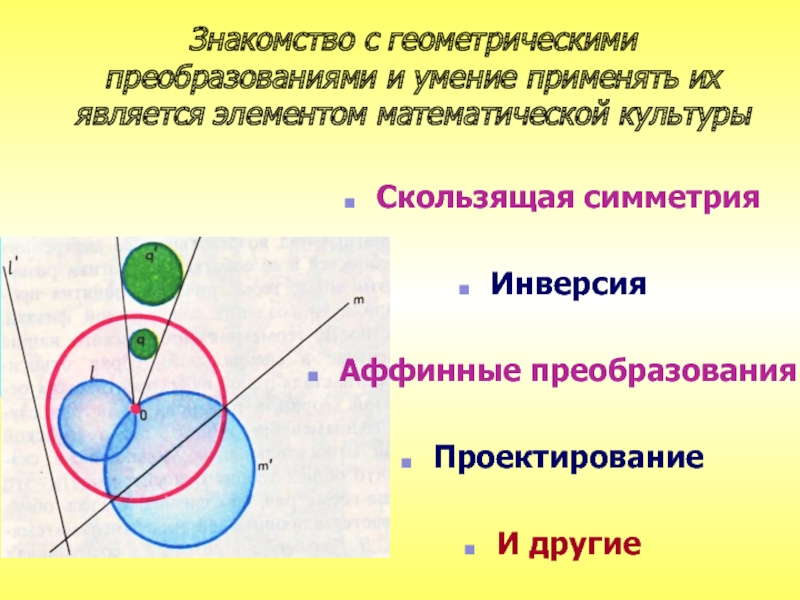
- 24. Знакомство с геометрическими преобразованиями и умение применять их является элементом математической культурыСкользящая симметрияИнверсияАффинные преобразованияПроектированиеИ другие
- 25. Скачать презентанцию
ДвижениеДвижениеПодобиеПараллельный переносПоворотСимметрияГомотетияПараллельноеОртогональноеГеометрическое преобразование плоскости это взаимно - однозначное отображение плоскости на себяПроектирование
Слайды и текст этой презентации
Слайд 2Движение
Движение
Подобие
Параллельный
перенос
Поворот
Симметрия
Гомотетия
Параллельное
Ортогональное
Геометрическое преобразование плоскости
это взаимно - однозначное отображение плоскости
на себя
Проектирование
Слайд 3х
у
z
о
м
м'
•
•
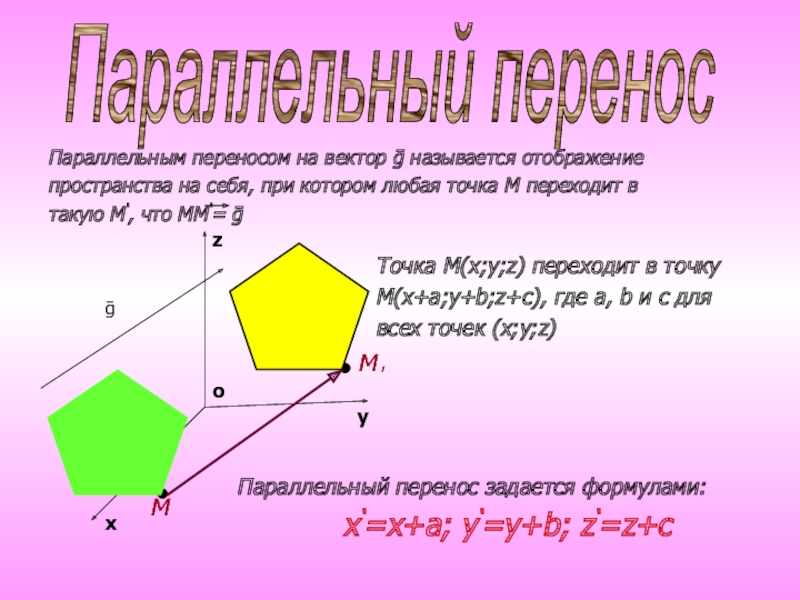
Точка М(х;у;z) переходит в точку
М(х+а;у+b;z+c), где а, b и
с для
всех точек (х;у;z)
Параллельный перенос задается формулами:
х‘=х+а; у‘=у+b; z‘=z+cḡ
Параллельным переносом на вектор ḡ называется отображение
пространства на себя, при котором любая точка М переходит в
такую М‘, что ММ‘= ḡ
Параллельный перенос
Слайд 4Параллельный перенос
х
у
z
о
Параллельный перенос
есть движение
Движение, сохраняющее направление,
является параллельным переносом
Слайд 5Поворотом плоскости около данной
точки называется такое движение,
при котором
каждый луч, исходящий
из этой точки, поворачивается на
один и
тот же угол в одном и том же направлении
β
– угол поворота
Точка О-центр поворота
х
х'
у
у'
β
поворот
о
Слайд 8
«Симметрия является
той идеей, посредством
которой человек на
протяжении
веков
пытается постичь и
создать порядок,
красоту и совершенство »
Г.ВейльЦентральная
симметрия
Осевая
симметрия
Зеркальная
симметрия
.
Симметрия
Слайд 9к1
к1
•
•
К
А1
А
•
•
Отображение пространства
на себя, при котором
любая точка А
переходит в симметричную
ей точку А1
относительно данного
центра О
о
Центральная
симметрия•
Слайд 12Осевой симметрией с осью
ℓ называется такое
отображение пространства
на себя, при
котором
любая точка М переходит
в симметричную ей точку
М1 относительно
оси ℓМ
М1
•
•
О
Осевая симметрия
ℓ
Слайд 14Осевая симметрия храмов
Церковь во имя апостола Андрея Первозванного
г. Ставрополь.
Церковь
Андрея Первозванного.
г. Ставрополь
Слайд 18Осевая симметрия в литературе
А
Ж
Э
Осевая симметрия в буквах
А, М, Т, Ш,
П имеют вертикальную
ось симметрии
В, З, К, С, Э, Е – горизонтальную ось симметрии
Ж, Н, О, Ф, Х имеют две оси симметрии
Осевая симметрия в словах
Казак
Шалаш
Осевая симметрия фраз
Искать такси
Аргентина манит негра
А роза упала на лапу Азора
Слайд 19Зеркальной симметрией(симметрией
относительно плоскости) называется такое
отображение пространства на себя,
при котором
любая точка Х переходит в симметричную
ей относительно
данной плоскости точку Х '
Зеркальная симметрия
● Х
● Х '
•
Слайд 21Преобразование фигуры F в фигуру F‘ называется преобразованием подобия, если
при этом преобразовании расстояние между точками изменяется в одно и
тоже число раз.А1В1=k∙АВ
С1Д1=k∙СД
k-КОЭФФИЦИЕНТ
ПОДОБИЯ
А1
А
В1
В
С1
С
Д1
Д
•
•
•
•
•
•
•
•
Подобие
Подобие
Подобие
Слайд 22Гомотетией с центром
О и коэффициентом
k≠0 называется
геометрическое преобразование,
которое произвольно
взятую точку А
переводит в такую точку
А‘,
что ОА‘=k∙ОА Гомотетия
Слайд 24Знакомство с геометрическими преобразованиями и умение применять их является элементом
математической культуры
Скользящая симметрия
Инверсия
Аффинные преобразования
Проектирование
И другие
Теги
