Геометрический смысл производной. Применение производной

Содержание

1. Геометрический смысл производной. Применение производной
2. Задание 1. ( В 8)
3. Задание 1. ( В 8) Решение.
4. Задание 2. ( В 8 )
5. Задание 2. ( В 8 ) Решение.
6. Задание 3. ( В 8 )
7. Задание 3. ( В 8 ) Решение.
8. Задание 4. ( В 8 )
9. Задание 4. ( В 8 )
10. Задание 5. ( В 8 )
11. Задание 5. ( В 8 )
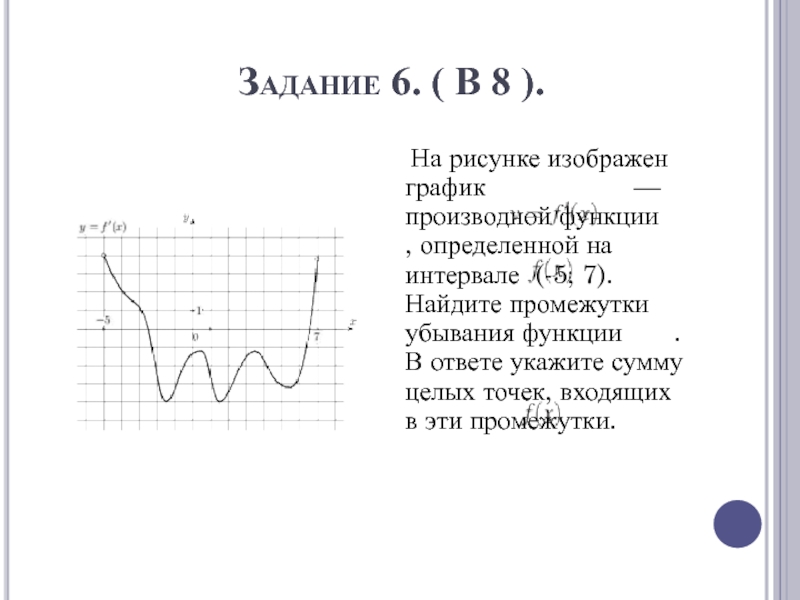
12. Задание 6. ( В 8 ).
13. Задание 6. ( В 8 ). Решение.
14. Скачать презентанцию

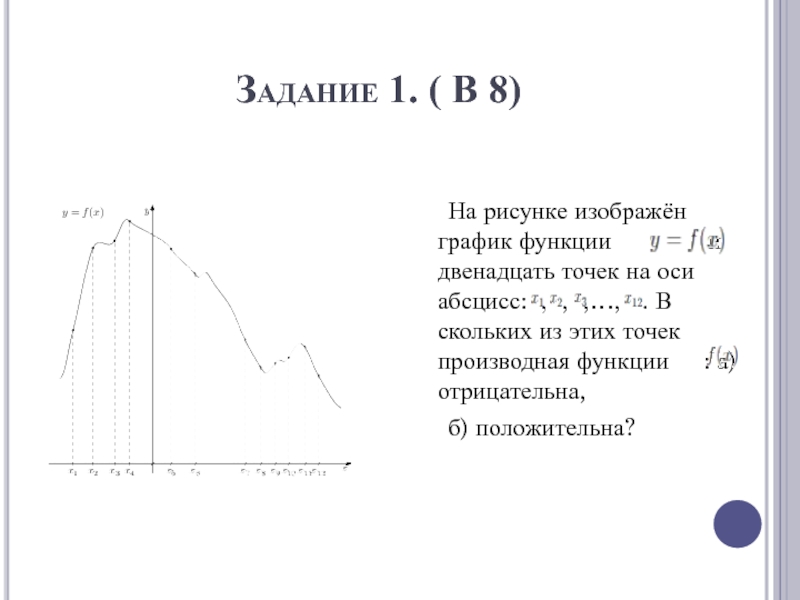
Задание 1. ( В 8) На рисунке изображён график функции и двенадцать точек на оси абсцисс: , , ,…, . В скольких

Главная
Математика
Геометрический смысл производной. Применение производной

Слайды и текст этой презентации

Слайд 1Итоговое повторение.
Геометрический смысл производной.
Применение производной.
2013-1014г
МБОУ СОШ № 10
г.

о. Железнодорожный Московская область
Учитель математики: Фарух Н. Е.

Итоговое повторение. Геометрический смысл производной. Применение производной.2013-1014гМБОУ СОШ № 10 г. о. Железнодорожный Московская областьУчитель математики:

Слайд 2Задание 1. ( В 8)

На рисунке изображён

график функции и двенадцать

точек на оси абсцисс: , , ,…, . В скольких из этих точек производная функции : а) отрицательна,
б) положительна?

Задание 1. ( В 8) На рисунке изображён график функции

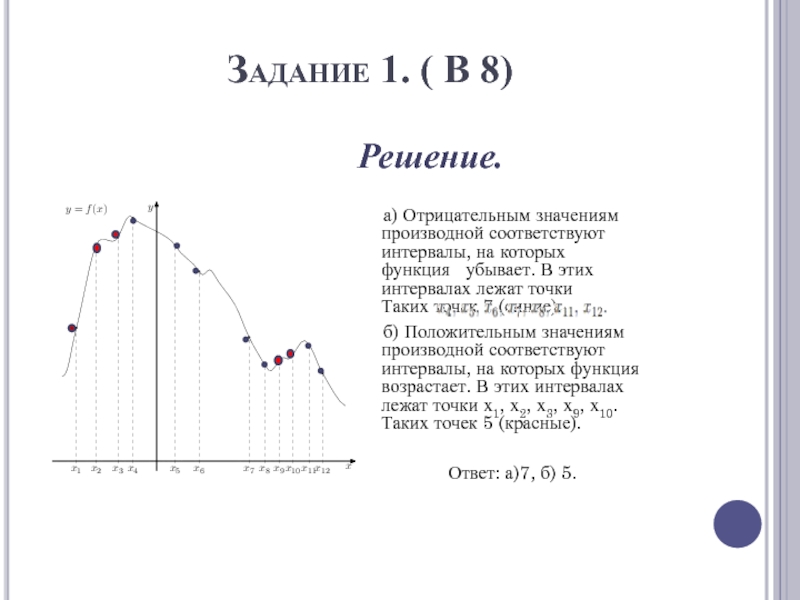
Слайд 3Задание 1. ( В 8)
Решение.

а)

Отрицательным значениям производной соответствуют интервалы, на которых функция убывает. В

этих интервалах лежат точки Таких точек 7 (синие).
б) Положительным значениям производной соответствуют интервалы, на которых функция возрастает. В этих интервалах лежат точки х1, х2, х3, х9, х10. Таких точек 5 (красные).

Ответ: а)7, б) 5.

Задание 1. ( В 8) Решение. а) Отрицательным значениям производной соответствуют интервалы, на

Слайд 4Задание 2. ( В 8 )

Прямая

параллельна касательной к графику функции

Найдите абсциссу точки касания.

Слайд 5Задание 2. ( В 8 )
Решение.
Значение производной в

точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна прямой

, их угловые коэффициенты равны. Поэтому абсцисса точки касания находится из уравнения :

Ответ: 0,5.

Задание 2. ( В 8 ) Решение. Значение производной в точке касания равно угловому коэффициенту касательной.

Слайд 6Задание 3. ( В 8 )
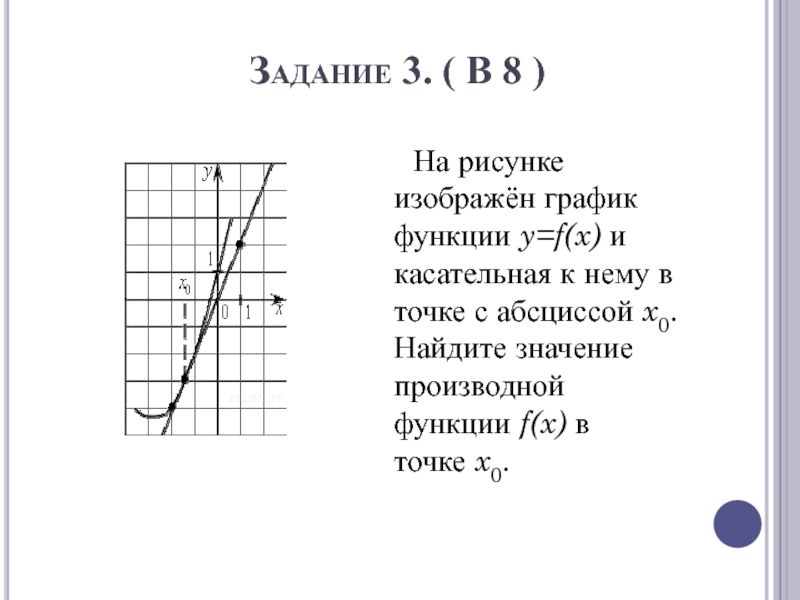
На рисунке

изображён график функции y=f(x) и касательная к нему в точке с абсциссой x0.

Найдите значение производной функции f(x) в точке x0.

Задание 3. ( В 8 ) На рисунке изображён график функции y=f(x) и касательная к

Слайд 7Задание 3. ( В 8 )

Решение.

Значение производной в

точке касания равно угловому коэффициенту касательной, который в свою очередь

равен тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (1; 2), B (1; −4), C(−2; −4). Угол наклона касательной к оси абсцисс будет равен тангенсу угла ACB

Ответ: 2.

Задание 3. ( В 8 ) Решение. Значение производной в точке касания равно угловому коэффициенту касательной,

Слайд 8Задание 4. ( В 8 )
На рисунке изображён

график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите

значение производной функции f(x) в точке x0.

Задание 4. ( В 8 ) На рисунке изображён график функции y=f(x) и касательная к нему

Слайд 9Задание 4. ( В 8 )
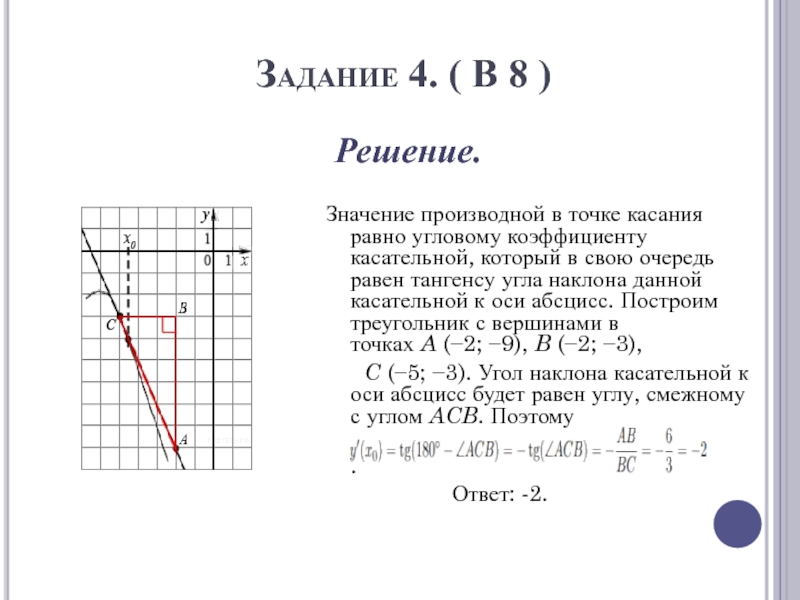
Решение.

Значение производной в точке

касания равно угловому коэффициенту касательной, который в свою очередь равен

тангенсу угла наклона данной касательной к оси абсцисс. Построим треугольник с вершинами в точках A (−2; −9), B (−2; −3),
C (−5; −3). Угол наклона касательной к оси абсцисс будет равен углу, смежному с углом ACB. Поэтому
.
Ответ: -2.

Задание 4. ( В 8 ) Решение.Значение производной в точке касания равно угловому коэффициенту касательной, который

Слайд 10Задание 5. ( В 8 )
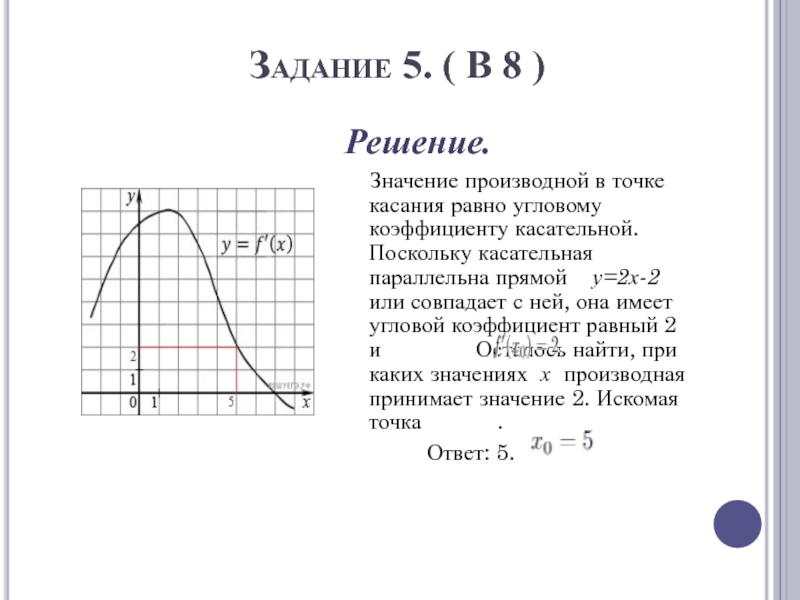
На рисунке изображен

график производной функции f(x) . Найдите абсциссу точки, в которой касательная

к графику y=f(x) параллельна прямой y=2x-2 или совпадает с ней.

Задание 5. ( В 8 ) На рисунке изображен график производной функции f(x) . Найдите

Слайд 11Задание 5. ( В 8 )
Решение.
Значение производной

в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна

прямой у=2х-2 или совпадает с ней, она имеет угловой коэффициент равный 2 и Осталось найти, при каких значениях х производная принимает значение 2. Искомая точка .
Ответ: 5.

Задание 5. ( В 8 ) Решение. Значение производной в точке касания равно угловому

Слайд 12Задание 6. ( В 8 ).
На рисунке изображен

график

— производной функции , определенной на интервале (-5; 7). Найдите промежутки убывания функции . В ответе укажите сумму целых точек, входящих в эти промежутки.