Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Готовимся к ЕГЭ Задание В13 Задачи на проценты
Содержание
- 1. Готовимся к ЕГЭ Задание В13 Задачи на проценты
- 2. «Я могу только показать тебе дверь,
- 3. Понятие о проценте.
- 4. Необходимо знать!
- 5. Простейшие задачи, связанные с понятием проценты.
- 6. Простейшие задачи, связанные с понятием проценты.
- 7. Простейшие задачи, связанные с понятием проценты. Простой процентный рост.
- 8. Слайд 8
- 9. Необходимо знать!
- 10. Слайд 10
- 11. Слайд 11
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Задачи на концентрацию, смеси, сплавы.Процентное содержание вещества
- 18. Простейшие задачи на концентрацию, смеси, сплавы.
- 19. Слайд 19
- 20. Слайд 20
- 21. Пример 25. Смешали 4 литра 15-процентного водного
- 22. Пример 26. Морская вода содержит 8% (по
- 23. Слайд 23
- 24. Пример 28. Виноград содержит 90% влаги, а
- 25. Пример 29. Имеются два слитка, содержащие медь
- 26. Слайд 26
- 27. Слайд 27
- 28. Для самостоятельного решения.Пример 32. В сосуд, содержащий
- 29. Ответы.
- 30. Слайд 30
- 31. Рекомендации по решению текстовых задач Не
- 32. ЛитератураСпецификация экзаменационной работы по математике единого государственного
- 33. Спасибо!
- 34. Скачать презентанцию
Слайды и текст этой презентации
Слайд 17Задачи на концентрацию, смеси, сплавы.
Процентное содержание вещества в растворе называют
концентрацией раствора.
Обычно, в условиях задач, решение которых связано с использованием
понятий «концентрация» и «процентное содержание», речь идет о составлении сплавов, растворов или смесей двух или нескольких веществ.Основные допущения, как правило, принимаемые в задачах подобного рода, состоят в следующем:
а) все получающиеся сплавы или смеси однородны;
б) при слиянии двух растворов, имеющих объемы V1 и V2, получается смесь, объем которой равен V1 + V2, т.е.
Vo = V1 + V2 причем,
последнее соотношение является именно допущением, поскольку не всегда выполняется в действительности: при слиянии двух растворов не объем, а масса смеси равняется сумме масс составляющих ее компонент.
При решении задач на смеси и сплавы обычно отслеживают изменения, происходящие с «чистым» веществом.
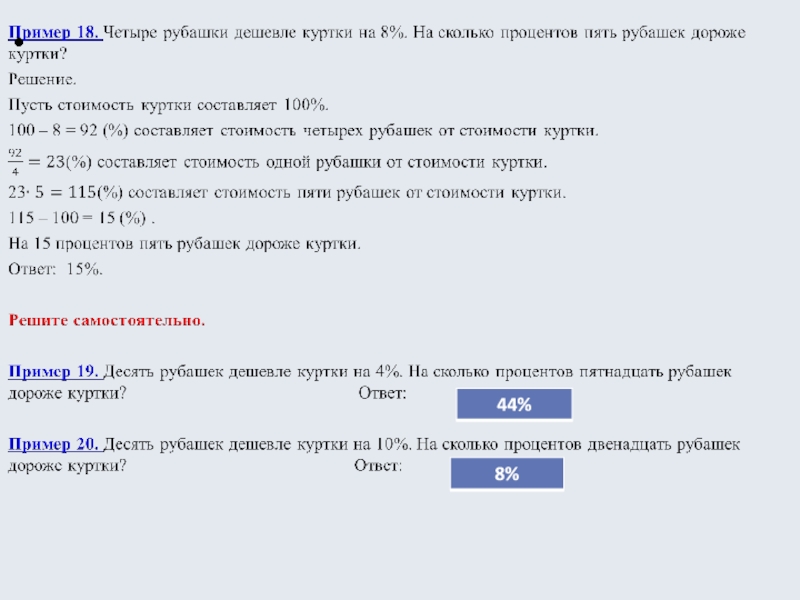
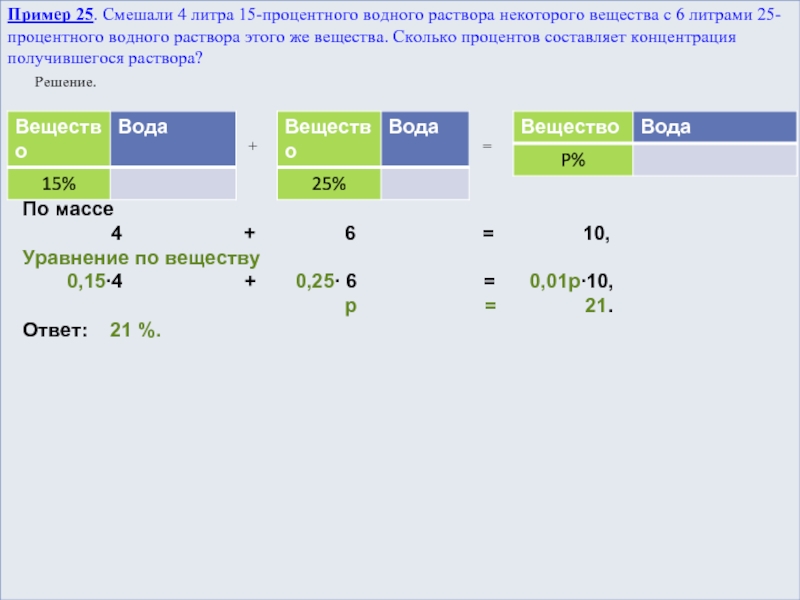
Слайд 21Пример 25. Смешали 4 литра 15-процентного водного раствора некоторого вещества
с 6 литрами 25-процентного водного раствора этого же вещества. Сколько
процентов составляет концентрация получившегося раствора?Решение.
+ =
По массе
4 + 6 = 10,
Уравнение по веществу
0,15∙4 + 0,25∙ 6 = 0,01p∙10,
p = 21.
Ответ: 21 %.
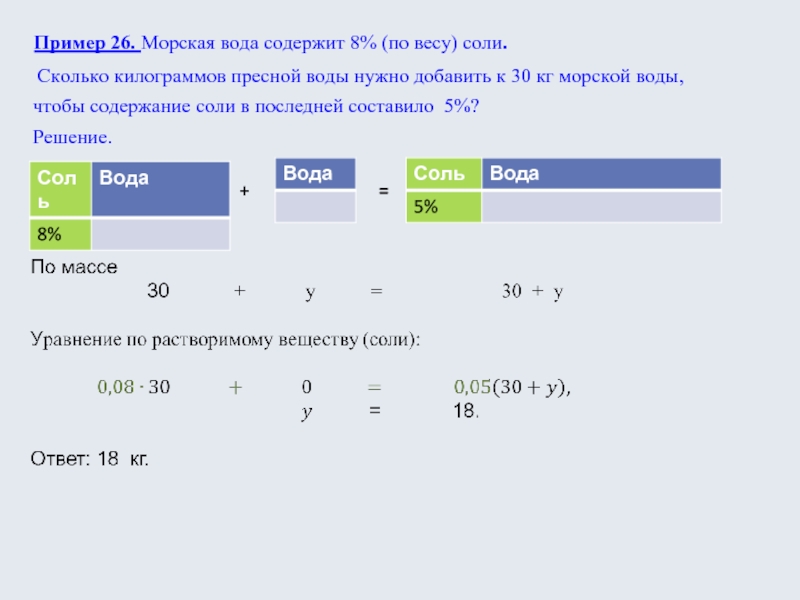
Слайд 22Пример 26. Морская вода содержит 8% (по весу) соли.
Сколько килограммов
пресной воды нужно добавить к 30 кг морской воды,
чтобы содержание
соли в последней составило 5%?Решение.
+
=
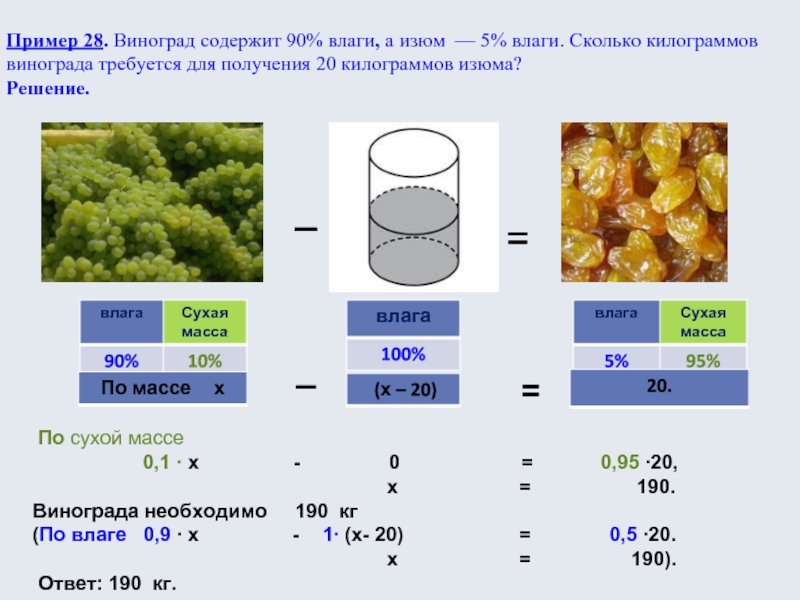
Слайд 24Пример 28. Виноград содержит 90% влаги, а изюм — 5%
влаги. Сколько килограммов винограда требуется для получения 20 килограммов изюма?
Решение.
_
=
_
=
По сухой массе0,1 ∙ х - 0 = 0,95 ∙20,
х = 190.
Винограда необходимо 190 кг
(По влаге 0,9 ∙ х - 1∙ (х- 20) = 0,5 ∙20.
х = 190).
Ответ: 190 кг.
Слайд 25Пример 29. Имеются два слитка, содержащие медь (Cu). Масса второго
слитка на 3 кг больше, чем масса первого слитка. Содержание
меди в первом слитке - 10%, во втором – 40%. Слитки сплавили. Процентное содержание меди в сплаве – 30%. Определить массу полученного слитка.Решение.
+
=
По массе х + (х+3) = (х +х+ 3),
По меди
0,1∙х + 0,4∙(х+3) = 0,3∙(х +х+ 3),
х = 3.
Масса полученного слитка 9 кг.
Ответ: 9 кг.
Слайд 28Для самостоятельного решения.
Пример 32. В сосуд, содержащий 7 литров 28-процентного
водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов
составляет концентрация получившегося раствора?Пример 33. В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Пример 34. В сосуд, содержащий 6 литров 11-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Пример 35. Смешали 3 литра 35-процентного водного раствора некоторого вещества с 12 литрами 15-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Пример 36. Смешали 8 литров 10-процентного водного раствора некоторого вещества с 12 литрами 40-процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Пример 37. Сколько килограммов воды нужно выпарить из 0,5т целлюлозной массы, содержащей 85% воды, чтобы получить массу с содержанием воды 75%?
Пример 38. Смешав 30-процентный и 60-процентный растворы кислоты и добавив 10 кг чистой воды, получили 36-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 41-процентный раствор кислоты. Сколько килограммов 30-процентного раствора использовали для получения смеси?
Пример 39. Имеются два раствора кислоты в воде – 62 – процентный и 93 - процентный. Эти растворы смешали и добавили 10 кг чистой воды. В результате получили 62 процентный раствор кислоты. Если бы вместо 10 кг чистой воды добавили 10 кг 50 - процентного раствора той же кислоты, то получили бы 67 - процентный раствор кислоты. Сколько килограммов 62 – процентного раствора использовали для получения смеси?
Пример 40. Имеется два сплава. Первый сплав содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
Пример 41. Смешали некоторое количество 20-процентного раствора некоторого вещества с таким же количеством 16-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пример 42. Смешали некоторое количество 16-процентного раствора некоторого вещества с таким же количеством 18-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?
Пример 43. Имеется два сплава. Первый содержит 5% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 225 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?
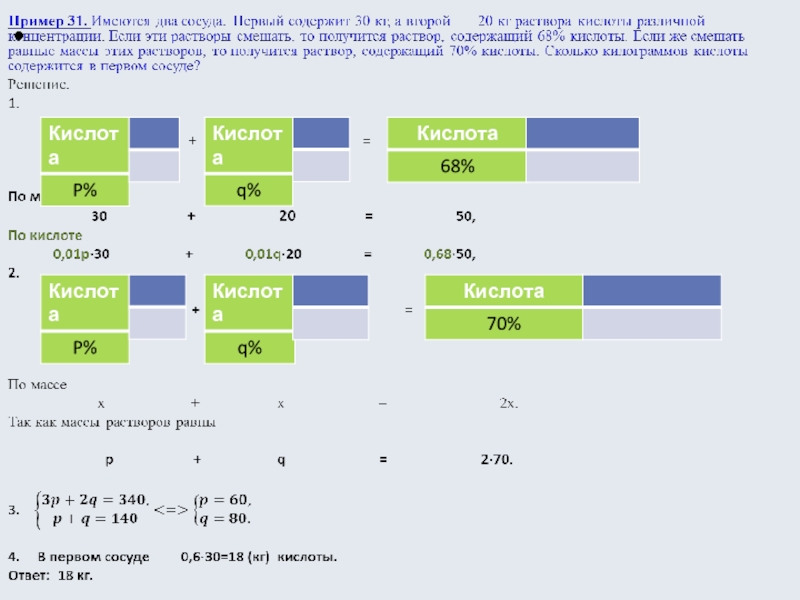
Пример 44. Имеется два сосуда. Первый содержит 100 кг, а второй — 60 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 19% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 22% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Слайд 30 Для того чтобы
научиться решать
текстовые задачи надо:
Решать разные типы задач с
разным уровнем сложности.Искать наиболее рациональные способы решения.
Пользоваться разными методами решения.
Решать как можно больше задач, как текстовых, так и других видов.
Слайд 31
Рекомендации по решению текстовых задач
Не просто прочитайте, а тщательно изучите
условие задачи.
Попытайтесь полученную информацию представить в другом виде
– это может быть рисунок, таблица или просто краткая запись условия задачи. Таблица является универсальным средством и позволяет решать большое количество идейно близких задач.Выбор неизвестных. Не надо бояться большого количества неизвестных или уравнений. Главное, чтобы они соответствовали условию задачи и, можно было составить соответствующую «математическую модель» (уравнение, неравенство, система уравнений или неравенств).
Составление и решение «математической модели». При составлении «математической модели» (уравнения,
неравенства, системы уравнений или неравенств) ещё раз внимательно прочитайте условие задачи.
Проследите за тем, что соответствует каждой фразе текста задачи в полученной математической записи
и чему в тексте задачи соответствует каждый «знак» полученной записи (сами неизвестные, действия над
ними, полученные уравнения, неравенства или их системы).
Очень важно не только составить уравнение, неравенство, систему уравнений или неравенств, но и решить его.
Если решение задачи не получается, то нужно ещё раз прочитать и проанализировать задачу (заданный текст и
полученную запись).
Иногда по условию задачи достаточно отыскать не сами неизвестные, а их комбинации. Например, не значения
неизвестных, а их сумму, разность и т.п.
Если получилось правильное, но очень сложное выражение, то попробуйте ввести другие неизвестные, может быть, изменив их количество, чтобы получилась более простая модель.
Иногда неизвестные в задачах выражаются только целыми числами, тогда при решении задач нужно использовать свойства целых чисел.
Решение сложной текстовой задачи – процесс творческий. Иной раз требуется вернуться к самому началу задачи, учитывая и анализируя уже полученные результаты.
Слайд 32Литература
Спецификация экзаменационной работы по математике единого государственного экзамена 2012 г.
Шестаков
С. А., Гущин Д. Д. ЕГЭ 2012. Математика. Задача В13.
Задачи на составление уравнений. Рабочая тетрадь / Под ред. А. Л. Семенова и И. В. Ященко.- 3-е изд., дополн. – М.: МЦНМО, 2012.Система дистанционной подготовки к ЕГЭ МИОО. Открытый банк заданий.
Левченко Н.П. Математика: Тренировочные задания тестовой формы с кратким ответом: рабочая тетрадь для учащихся общеобразовательных учреждений. (Практикум для подготовки к ЕГЭ.) М.: Вентана-Граф, 2008.
Семенов П.В. Алгебра и начала анализа: учеб. пособие. (ЕГЭ: шаг за шагом.) М.: Мнемозина, 2010.
Семенов П.В. Математика 2008. Выпуск 4. Текстовые и геометрические задачи. Задачи с развернутым ответом. (Как нам подготовиться к ЕГЭ.) М.: МЦНМО, 2008.
Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену. (Домашний репетитор.) М.: Айрис-пресс, 2011.
Юрченко Е.В. Математика. Тематическая рабочая тетрадь для восстановления базовых знаний. Части, отношения, пропорции, проценты. (Тематические тетради.) М.: Айрис-пресс, 2007.
М.Л.Галицкий, А.М.Гольдман, Л.И.Звавич Сборник задач по алгебре 8-9 класс
Москва «Просвещение» 2010 год
Е.Д.Куланин, В.П.Норин, С.Н.Фезин, Ю. А. Шевченко 3000 конкурсных задач по математике. Москва «Мартин» 2010 год
С.В.Кравцев, Ю.Н.Макаров, В.Ф.Максимов Методы решения задач по алгебре. Москва «ОНИКС 21 век» 2006 год
М.И.Сканави Сборник задач для поступающих в ВУЗы Москва «Мир и Образование» 2010 год