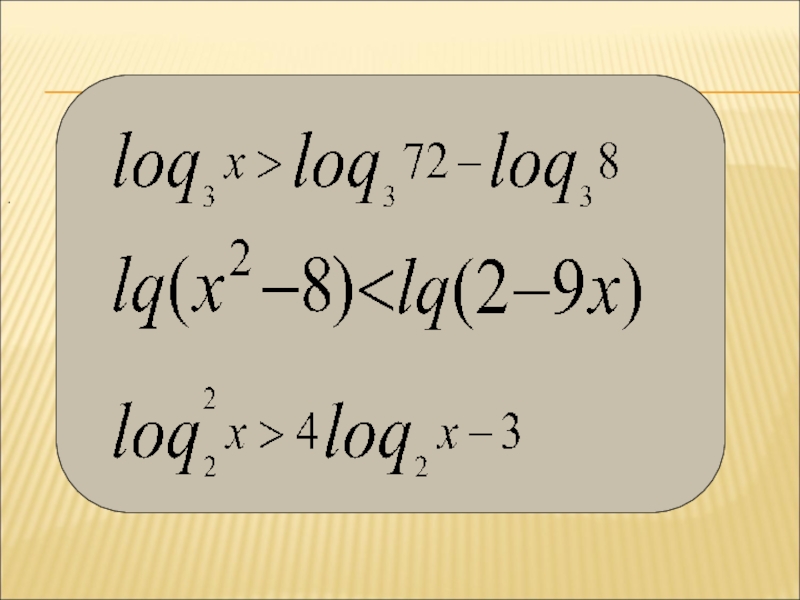Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ.
Содержание
- 1. РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ.
- 2. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯУравнения, содержащие неизвестное под знаком логарифма или в основании логарифма называются логарифмическими.
- 3. Решение уравнений, содержащих неизвестное под знаком логарифма, основано на следующих теоремах:
- 4. Слайд 4
- 5. ВЫБЕРИ МЕТОД РЕШЕНИЯ УРАВНЕНИЯ
- 6. РЕШИТЕ УРАВНЕНИЯ;.
- 7. НАЙТИ КОРНИ УРАВНЕНИЯ;.
- 8. ДЛЯ РЕШЕНИЯ ЛУ ГРАФИЧЕСКИМ МЕТОДОМ НАДО ПОСТРОИТЬ
- 9. Слайд 9
- 10. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВАРешение неравенств, содержащих неизвестное под знаком логарифма, основано на следующих теоремах:
- 11. РЕШИТЕ НЕРАВЕНСТВА1 .
- 12. .
- 13. ЛОГАРИФМИЧЕСКАЯ «КОМЕДИЯ 2>3»Комедия начинается с неравенства,
- 14. Скачать презентанцию
ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯУравнения, содержащие неизвестное под знаком логарифма или в основании логарифма называются логарифмическими.
Слайды и текст этой презентации
Слайд 1РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ. УЧИТЕЛЬ МАТЕМАТИКИ МБОУ СОШ С. БЕРЕЗОВКА
1-Я ПОРТНОВА С.Ю.
Слайд 2ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
Уравнения, содержащие неизвестное под знаком логарифма или в основании
логарифма называются логарифмическими.
Слайд 3
Решение уравнений, содержащих неизвестное под знаком логарифма, основано на следующих
теоремах:
Слайд 8
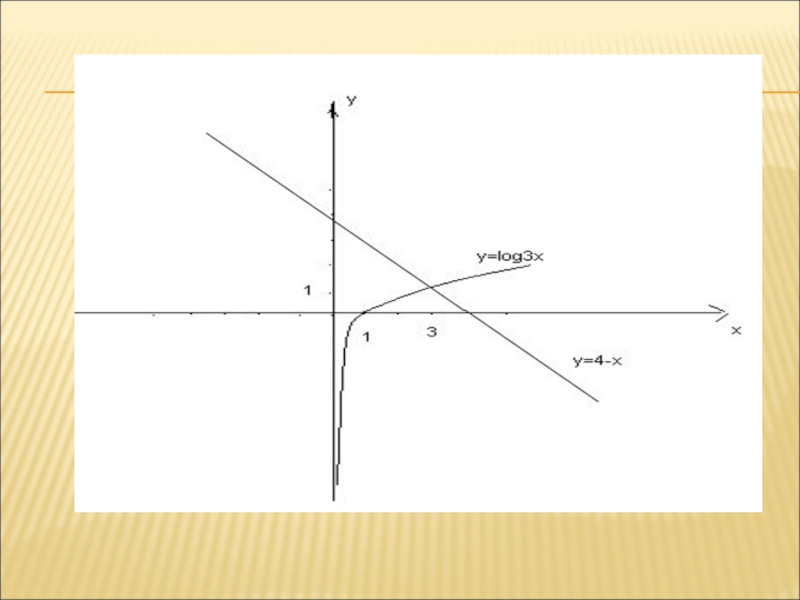
ДЛЯ РЕШЕНИЯ ЛУ ГРАФИЧЕСКИМ МЕТОДОМ НАДО ПОСТРОИТЬ В ОДНОЙ И
ТОЙ ЖЕ СИСТЕМЕ КООРДИНАТ ГРАФИКИ ФУНКЦИЙ, СТОЯЩИХ В ЛЕВОЙ И
ПРАВОЙ ЧАСТЯХ УРАВНЕНИЯ И НАЙТИ АБСЦИССУ ИХ ТОЧКИ ПЕРЕСЕЧЕНИЯ Найти корни уравнения
Так как функция у= log3 х возрастающая, а функция у =4-х убывающая на (0; + ∞ ),то заданное уравнение на этом интервале имеет один корень.
Слайд 10
ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
Решение неравенств, содержащих неизвестное под знаком логарифма, основано на
следующих теоремах:
Слайд 13
ЛОГАРИФМИЧЕСКАЯ «КОМЕДИЯ 2>3»
Комедия начинается с неравенства,
бесспорно правильного.
Затем
следует преобразование
тоже не внушающее сомнения
Большему числу соответствует больший
логарифм, если функция возрастает, значит,После сокращения на
Имеем 2>3.
В чем ошибка этого доказательства?