Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Задачи на прогрессии
Содержание
- 1. Задачи на прогрессии
- 2. Задачи на прогрессииПоследовательность каждый член которой,
- 3. Арифметическая прогрессияФормула n-ого члена арифметической прогрессииФормула суммы
- 4. Характеристическое свойство (признак) арифметической прогрессии:
- 5. Геометрическая прогрессия Последовательность, первый член
- 6. Называется n-ым членом последовательностиФормула n-ого члена геометрической
- 7. Геометрическая прогрессия, у которой
- 8. Задача 1 Продавец киоска обратил внимание
- 9. Решение Количество открыток, продаваемых продавцом, изменяется
- 10. Значит, составим и решим систему уравненийТак кактоТак
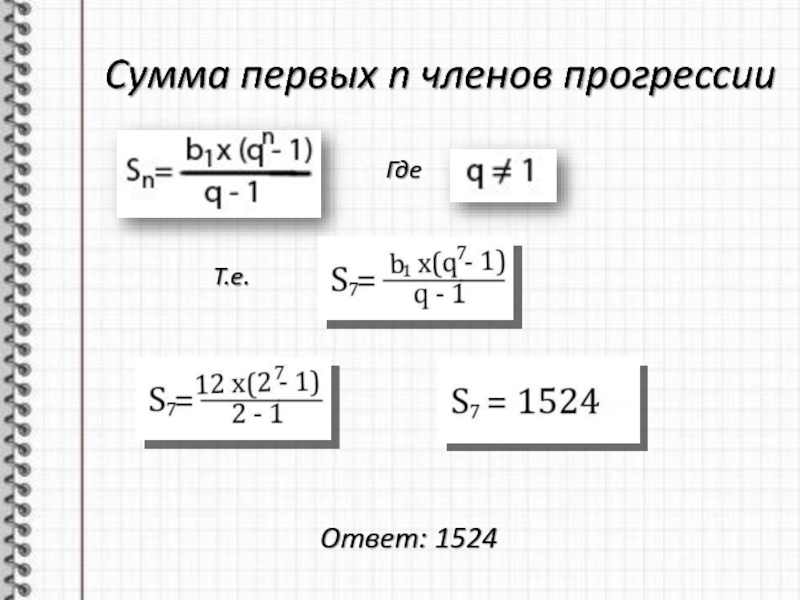
- 11. Сумма первых n членов прогрессииГдеТ.е.Ответ: 1524
- 12. Задача 2 Если положить на вклад
- 13. РешениеПо условию х=10%,
- 14. Задача 3 В первый год строительства
- 15. РешениеКоличество жителей, прибывших в микрорайон, изменяется по
- 16. Задачи для самостоятельного решения1. В несколько колб
- 17. 2. На каждый из нескольких опытных участков
- 18. 3. Компьютерная игра в последовательном прохождении нескольких
- 19. 4. Первоначальная цена товара на торгах повышалась
- 20. 5. При подготовке к экзаменам ученик каждый
- 21. 6. В течении календарного года зарплата каждый
- 22. 7. Хозяин магазина заметил, что из года
- 23. 8. В микрорайоне проживало 1544 человека. В
- 24. 9. Первоначальная цена товара на торгах повышалась
- 25. 10. При подготовке к экзамену ученик каждый
- 26. Скачать презентанцию
Задачи на прогрессииПоследовательность каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же постоянным для данной последовательности числом d, называется арифметической прогрессией
Слайды и текст этой презентации
Слайд 1Презентацию выполнила ученица 593 школы
10-1 класса
Зубова Кристина
Учитель:
Петрова Наталья Васильевна
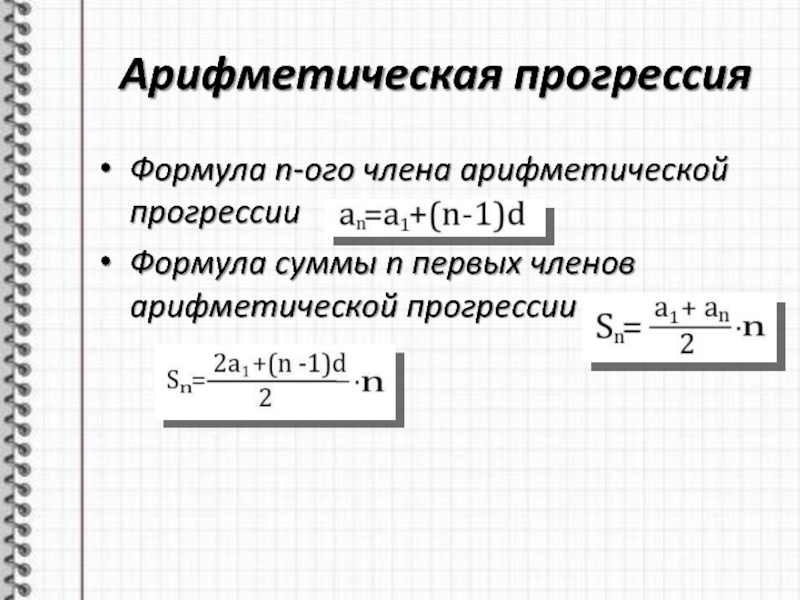
Слайд 3Арифметическая прогрессия
Формула n-ого члена арифметической прогрессии
Формула суммы n первых членов
арифметической прогрессии
Слайд 4 Характеристическое свойство (признак) арифметической прогрессии: каждый член арифметической
прогрессии, начиная со второго, есть среднее арифметическое соседних с ним
членовгде
Слайд 5Геометрическая прогрессия
Последовательность,
первый член которой
отличен
от нуля, и каждый член, начиная со второго, равен предыдущему,
умноженному на одно и тоже, отличное от нуля, постоянное для данной последовательности число q, называется геометрической прогрессии.Число q - знаменатель прогрессии
Слайд 6Называется n-ым членом последовательности
Формула n-ого члена геометрической прогрессии имеет вид
Формула
суммы n первых членов геометрической прогрессии имеет вид
или
если
Слайд 7Геометрическая прогрессия, у которой
называется бесконечно убывающей
Сумма
бесконечно убывающей геометрической прогрессии имеет видгде
Слайд 8Задача 1
Продавец киоска обратил внимание на то, что
каждый год в последние 7 дней перед 8 марта количество
продаваемых в день поздравительных открыток увеличивается в одно и тоже число раз по сравнению с предыдущим днём. Начав торговать открытками за 7 дней перед праздником, он подсчитал, что в третий день было продано 48 открыток, а в пятый день – 192 открытки. Сколько всего открыток будет продано за 7 дней торговли, если замеченная продавцом закономерность сохраняется?Слайд 9Решение
Количество открыток, продаваемых продавцом, изменяется по закону геометрической
прогрессии. При этом
где x
> 0 и q > 1, так как прогрессия является возрастающей, используюя формулу n-ого члена геометрической прогрессии, имеемПо условию
Слайд 12Задача 2
Если положить на вклад «Накопительный» некоторую сумму
денег, то ежегодно она увеличивается на 10% от имеющейся на
вкладе суммы. Вкладчик положил на вклад «Накопительный» 30000 рублей и три года подряд пополнял свой вклад и не снимал с него денег. Определите, на сколько рублей увеличился его вклад за эти три годаСлайд 14Задача 3
В первый год строительства нового микрорайона в
него прибыло 250 жителей.
Районная управа планирует, что по
мере сдачи новых домов число прибывших жителей ежегодно будет увеличиваться в1,4 раза по сравнению с прошлым годом. Сколько жителей поселится в микрорайоне по данному плану за первые четыре года строительства?
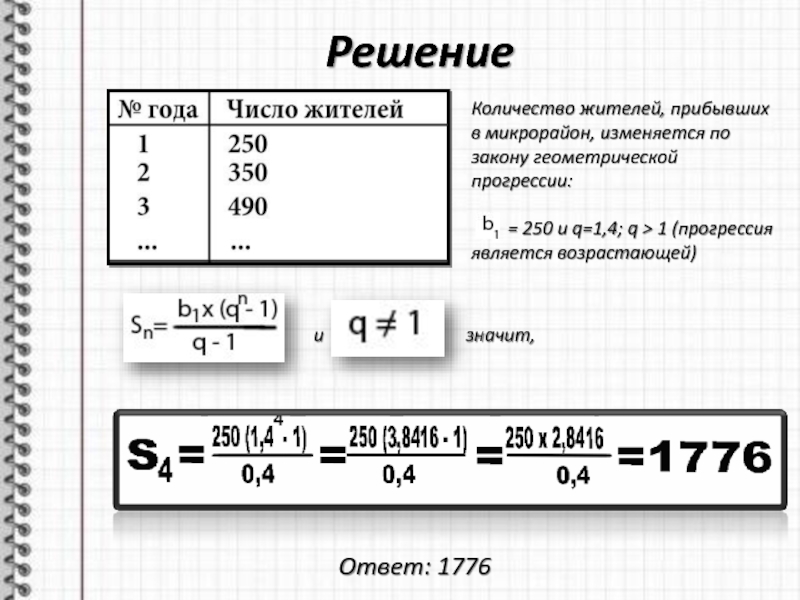
Слайд 15Решение
Количество жителей, прибывших в микрорайон, изменяется по закону геометрической прогрессии:
= 250 и q=1,4; q > 1
(прогрессия является возрастающей)и значит,
Ответ: 1776
Слайд 16Задачи для самостоятельного решения
1. В несколько колб вылили две кислоты.
Первую кислоту наливали по 12 мл в каждую колбу. Вторую
кислоту наливали в те же колбы по такой схеме: 3 мл в первую колбу, а в каждую последующую на 3 мл больше, чем в предыдущую. Всего разлили 285 мл кислоты. Сколько миллилитров кислоты налили в последнюю колбу?Ответ: 42 мл
Слайд 172. На каждый из нескольких опытных участков внесли по два
удобрения. Первое вносили по 3,5 кг на каждый участок. Второе
удобрение вносили по такой схем: 05, кг на первый участок, а на каждый следующий участок на 05, кг больше. Чем на предыдущий. Всего внесли 46 кг удобрений. Сколько килограммов удобрений внесли на последний участок?Ответ: 7,5 кг
Слайд 183. Компьютерная игра в последовательном прохождении нескольких уровней. За прохождение
каждого уровня игрок получает 10 баллов. Кроме того, начисляются премиальные
баллы по следующей схеме: 4 балла за второй уровень, а за каждый следующий уровень на 4 балла больше, чем за предыдущий. Сколько уровней надо пройти, чтобы набрать ровно 570?Ответ: 15 уровней
Слайд 194. Первоначальная цена товара на торгах повышалась несколько раз на
одно и тоже количество рублей. После третьего повышения цена равнялась
1200 рублей, а после двенадцатого повышения – 1650 рублей. Через сколько повышений первоначальная цена удвоилась?Ответ: 21
Слайд 205. При подготовке к экзаменам ученик каждый день с 1
по 8 июня включительно увеличивал количество решенных задач на одно
и тоже число. С 1 июня по 4 июня включительно он решил 24 задачи, а со 2 по 6 июня – 45 задач. Сколько задач ученик решил 8 июня?Ответ: 17 задач
Слайд 216. В течении календарного года зарплата каждый месяц повышалась на
одно и тоже число рублей. За июнь, июль, август зарплата
в сумме составила 9900 рублей, а сентябрь, октябрь, ноябрь – 10350 рублей. Найдите сумму зарплат за весь год.Ответ: 39300 рублей
Слайд 227. Хозяин магазина заметил, что из года в год в
последние 7 дней декабря число продаваемых в день новогодних наборов
увеличивается в 4 раза по сравнению с предыдущим днём. Начав торговлю наборами за 7 дней перед Новым годом, он подсчитал, что за первые два дня было продано всего 10 наборов. Сколько наборов будет продано за первые 6 дней, если замеченная хозяином закономерность сохраняется?Ответ: 2730
Слайд 238. В микрорайоне проживало 1544 человека. В первый год строительство
новых домов прибыло 400 новоселов. Планируется, что каждый год будут
строится новые дома, и число новоселов ежегодно будет увеличиваться в 1,2 раза по сравнению с предыдущим годом. Через сколько лет по данному плану в микрорайоне будет проживать 3000 человек?Ответ: 3 года
Слайд 249. Первоначальная цена товара на торгах повышалась несколько раз на
одно и тоже количество рублей. После четвертого повышения цена равнялась
1250 рублей. А после двадцать первого повышения она стала в два раза больше первоначальной цены, и торги закончились. Какова была предпоследняя цена?Ответ: 2050
Слайд 2510. При подготовке к экзамену ученик каждый день увеличивал количество
решенных задач на одно и тоже число. С 3 мая
по 6 мая включительно он решил 24 задачи, а с 5 по 10 мая – 72 задачи. Сколько задач ученик решил с 3 по 10 мая включительно?Ответ: 80 задач
Теги