Презентация по математике "Периоды развития геометрии"

примерно до V в. до н. э. и связан с

развитием культуры землемерия в древнем Египте, Вавилонии и Греции.
Религиозные обряды связывались с построением жертвенников, практические потребности людей приводили к необходимости измерения площадей земельных участков, объемов (емкости) сосудов, корзин и зернохранилищ.
Геометрические сведения и факты в основном сводились к правилам о вычислении площадей и объемов, и надо полагать, что эти правила носили больше эмпирический, чем логический характер.

мнению греческих историков, перенесены из Египта и Вавилонии в Грецию.

Греческие философы стали знакомиться с египетской и вавилонской мудростью. С этого времени начинается второй период развития геометрии — период систематического изложения геометрии как науки, где все предложения доказывались. К этому периоду были уже известны в Греции теоремы Фалеса (VI в. до н. э.). Фалес путешествовал в Египет и заимствовал сведения по геометрии и астрономии у жрецов о сумме углов в треугольнике, о вписанном угле и др.

Фалес (640/624—548/545 до н. э.)— древнегреческий философ и математик из Милета (Малая Азия). Представитель ионической натурфилософии и основатель милетской (ионийской) школы, с которой начинается история европейской науки. Именем Фалеса названа геометрическая теорема.

перспективой. Пифагор открывает несоизмеримые отрезки (иррациональные числа), доказывает теорему, носящую

его имя. Гиппократ Хиосский (V в. до н. э.) — последователь Пифагора — изложил систематически геометрию («Элементы» геометрии) и определил площадь луночки.

Анаксагор из Клазомен ( 500—428 гг. до н. э.) — древнегреческий философ, математик и астроном, основоположник афинской философской школы.

Гиппократ Хиосский (вторая половина V в. до н. э.) — древнегреческий математик и астроном. Основная научная заслуга Гиппократа — составление первого полного свода геометрических знаний.

Пифагор Самосский ( 570—490 гг. до н. э.) — древнегреческий философ и математик, создатель религиозно-философской школы пифагорейцев.

хотя и не оставили никаких трудов по геометрии, но придавали

большое значение системе и обоснованию геометрии, они положили начало определениям и аксиомам.

Платон (428 или 427 до н. э. — 348 или 347 до н. э.) — древнегреческий философ, ученик Сократа, учитель Аристотеля. Основные интересы: метафизика, эпистемология, этика, эстетика, политика, образование, философия математики.

Аристотель (384—322 гг. до н. э) — древнегреческий философ и учёный. Ученик Платона. С 343 до н. э. — воспитатель Александра Македонского. В 335/4 г. до н. э. основал Ликей (Лицей, или перипатетическую школу). Основоположник формальной логики. Создал понятийный аппарат, который до сих пор пронизывает философский лексикон и сам стиль научного мышления.

было ее систематизировать. Таким систематизатором был Евклид (III в. до

н. э.), изложивший геометрию (элементарную) на базе основных предложений — аксиом в своих знаменитых книгах «Начала» (элементы), содержащих 13 томов.

Евклид или Эвклид (ок. 300 г. до н. э.) — древнегреческий математик. Историческая заслуга Евклида состоит в том, что он, создавая свои “Начала”, объединил результаты своих предшественников, упорядочил и привел в одну систему основные геометрические знания того времени.

Ватиканский манускрипт, т.1, 38v - 39r. Euclid I prop. 47 (теорема Пифагора).

одним ученым. Известно, что Евклид в своей работе опирался на

труды десятков предшественников, среди которых были Фалес и Пифагор, Демокрит и Гиппократ, Архит, Теэтет, Евдокс и др. Историческая заслуга Евклида состоит в том, что он, создавая свои “Начала”, объединил результаты своих предшественников, упорядочил и привел в одну систему основные геометрические знания того времени. На протяжении двух тысячелетий геометрия изучалась в том объеме, порядке и стиле, как она была изложена в “Началах” Евклида. Многие учебники элементарной геометрии во всем мире представляли (а многие и поныне представляют) собой лишь переработку книги Евклида. “Начала” на протяжении веков были настольной книгой величайших ученых.

Аполлоний, Эратосфен (III в. до н. э.) и др., которые

обогатили геометрию новыми открытиями.

Архимед (287— 212 гг. до н. э.) — древнегреческий математик, физик, механик и инженер из Сиракуз. Сделал множество открытий в геометрии. Заложил основы механики, гидростатики, автор ряда важных изобретений. Главные математические достижения Архимеда касаются проблем, которые сейчас относят к области математического анализа.

Аполлоний Пергский (262—190 гг. до н. э.) — один из трёх (наряду с Евклидом и Архимедом) великих геометров античности, живших в III веке до н. э. Аполлоний дал содержательную общую теорию эллипса, параболы и гиперболы, ввёл и другие математические термины: асимптота, абсцисса, ордината, аппликата.

Эратосфен Киренский (276—194 гг. до н. э.) — греческий математик, астроном, географ и поэт. С 235 г. до н. э. — глава Александрийской библиотеки. Эратосфеном найден способ определения произвольного количества последовательных простых чисел (так называемое решето Эратосфена).

геометрии — созданию в первой половине XVII в. аналитической геометрии,

творцами которой были Декарт и Ферма. Аналитическая геометрия изучает свойства геометрических фигур по их алгебраическим уравнениям, опираясь на метод координат.

Рене Декарт (1596—1650)—французский математик, философ, физик и физиолог, создатель аналитической геометрии и современной алгебраической символики, автор метода радикального сомнения в философии, механицизма в физике, предтеча рефлексологии.

Пьер де Ферма (1601—1665)—французский математик, один из создателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. По профессии юрист, с 1631 года — советник парламента в Тулузе. Блестящий полиглот. Наиболее известен формулировкой Великой теоремы Ферма.

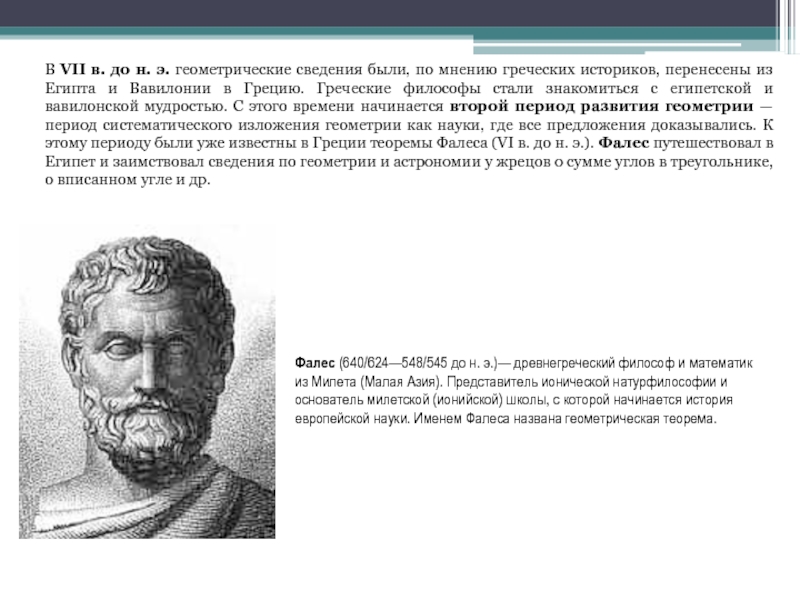
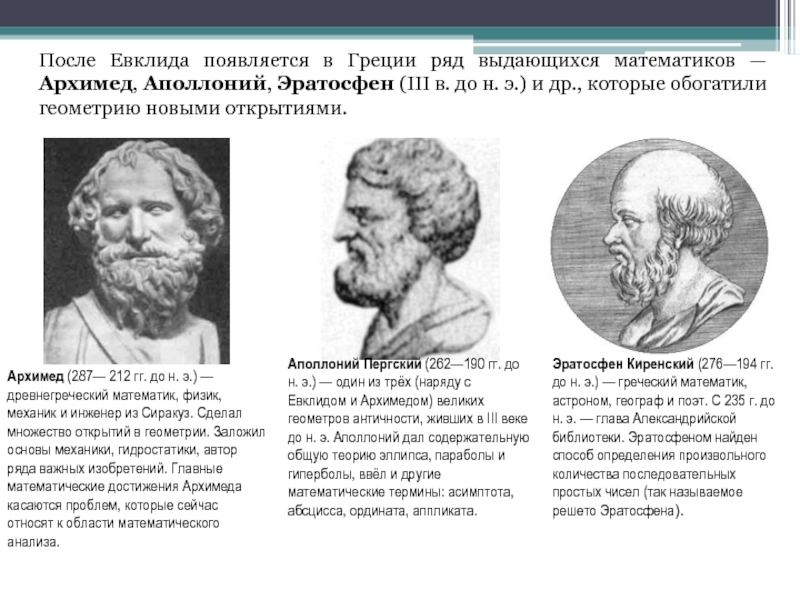
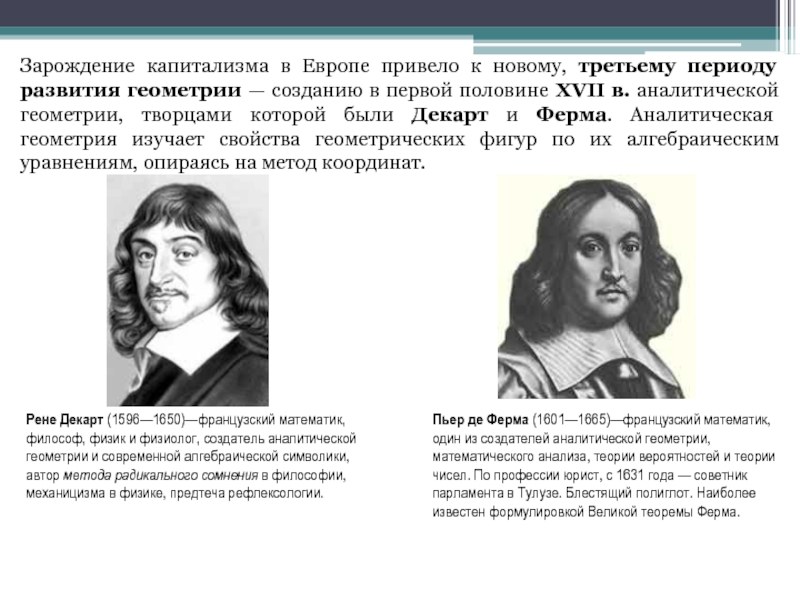
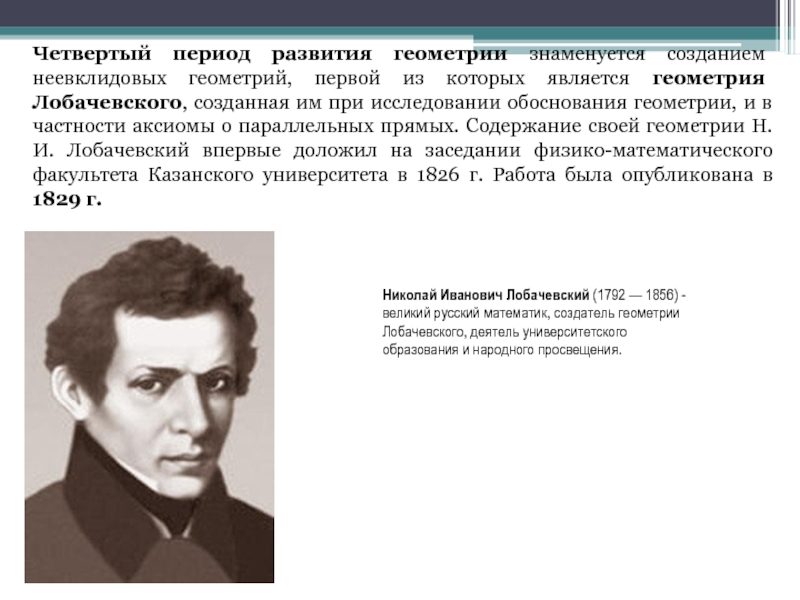
фигур локального характера (в окрестности данной точки) возникла в XVIII

в. дифференциальная геометрия в работах Эйлера, Монжа. Развитие военного дела и архитектуры привело к разработке методов точного изображения пространственных фигур на плоском чертеже, в связи с чем появляются начертательная геометрия, научные основы которой заложил французский математик Монж.

Леонард Эйлер (1707-1783)— российский и швейцарский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук. Эйлер впервые увязал анализ, алгебру, тригонометрию, теорию чисел и др. дисциплины в единую систему, и добавил немало собственных открытий.

Гаспар Монж (1746—1818)— французский математик, геометр, создатель «Начертательной геометрии». Его работы по теории поверхностей, помимо своего непосредственного значения, повели к выяснению важного принципа непрерывности и к раскрытию смысла той широкой неопределенности, которая порождается при интегрировании уравнений с частными производными, произвольными постоянными и ещё более появлением произвольных функций.

половине XVII в. проективная геометрия, которая возникла сначала при изучении

изображения перспективы, а затем при изучении тех свойств фигур, которые не изменяются при проектировании с одной плоскости на другую из какой-либо точки пространства (центральное проектирование), и впоследствии была завершена в трудах Ж. Понселе.

Жерар Дезарг (1591—1661)—французский геометр. Получил известность трактатом о конических сечениях. Основатель проективной геометрии.

Блез Паскаль (1623—1662)—французский математик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики.

Жан Виктор Понселе (1788–1867)—математик и инженер, создатель проективной геометрии, один из основоположников изучения свойства усталости материалов в разделе физики материаловедение.

которых является геометрия Лобачевского, созданная им при исследовании обоснования геометрии,

и в частности аксиомы о параллельных прямых. Содержание своей геометрии Н. И. Лобачевский впервые доложил на заседании физико-математического факультета Казанского университета в 1826 г. Работа была опубликована в 1829 г.

Николай Иванович Лобачевский (1792 — 1856) - великий русский математик, создатель геометрии Лобачевского, деятель университетского образования и народного просвещения.

в 1832 г. и в менее развитой форме. Открытие Лобачевского

было началом нового периода в развитии геометрии. За ним последовали новые открытия немецкого математика Бернхарда Римана. Те же идеи развивал Карл Гаусс, но он не опубликовал их.

Янош Бойяи (1802—1860)— венгерский математик, один из первооткрывателей неевклидовой геометрии (называемой теперь геометрией Лобачевского).

Бернхард Риман (1826—1866) — немецкий математик. Риман определил общее понятие n-мерного многообразия и его метрику. Риман также высказал предположение, что геометрия в микромире может отличаться от трёхмерной евклидовой.

Карл Гаусс (1777—1855) — великий немецкий математик, астроном и
физик, считается одним из
величайших математиков всех
времён. Гаусс впервые начал изучать
внутреннюю геометрию
поверхностей, опубликовал труды по
дифференциальной геометрии.

математики. Одним из источников развития и образования новых понятий в

геометрии, как и в других областях математики, являются современные задачи естествознания, физики и техники. Геометрия превратилась в разветвленную и быстро развивающуюся в разных направлениях совокупность математических теорий, изучающих разные пространства (евклидово, лобачевского, проективное, римановы и т.д.) и фигуры в этих пространствах.