Графа и его элементы

Содержание

1. Графа и его элементы
2. ГРАФОМ G =
3. ТОЧКИ НАЗЫВАЮТСЯ ВЕРШИНАМИ, ИЛИ УЗЛАМИ, ГРАФА, ЛИНИИ – РЕБРАМИ ГРАФА.ПРИМЕРЫ ГРАФОВ
4. ЕСЛИ РЕБРО ГРАФА СОЕДИНЯЕТ ДВЕ ЕГО ВЕРШИНЫ,
5. КРАТНЫЕ РЕБРАЧИСЛО РЕБЕР, ИНЦИДЕНТНЫХ ВЕРШИНЕ A ,
6. deg(E) = 0E – ИЗОЛИРОВАННАЯ ВЕРШИНАdeg(G) =
7. ТЕОРЕМАВ ГРАФЕ G(V, X) СУММА СТЕПЕНЕЙ ВСЕХ
8. ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО
9. ОРГРАФДУГИНАЧАЛО ДУГИ (A,B)КОНЕЦ ДУГИ (A,B)СТЕПЕНЬЮ ВХОДА (ВЫХОДА)
10. ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР НЕОРИЕНТИРОВАННОГО
11. ПУТЬ – УПОРЯДОЧЕННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР ОРИЕНТИРОВАННОГО ГРАФА,
12. ЦЕПЬ, ПУТЬ И ЦИКЛ В ГРАФЕ НАЗЫВАЮТСЯ
13. ГРАФ G НАЗЫВАЕТСЯ ПЛАНАРНЫМ(ПЛОСКИМ), ЕСЛИ СУЩЕСТВУЕТ ТАКОЙ
14. ЭЙЛЕРОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), КОТОРЫЙ СОДЕРЖИТ
15. ГАМИЛЬТОНОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), ПРОХОДЯЩИЙ ЧЕРЕЗ
16. МАТРИЦЕЙ ИНЦИДЕНТНОСТИ ГРАФА G НАЗЫВАЮТ ТАБЛИЦУ B,
17. МАТРИЦЕЙ СМЕЖНОСТИ ГРАФА G(V,X) БЕЗ КРАТНЫХ РЕБЕР
18. ЗАДАЙТЕ СЛЕДУЮЩИЙ ОРГРАФ ТАБЛИЦЕЙ ИНЦИДЕНТНОСТИ
19. ЗАДАЙТЕ СЛЕДУЮЩИЙ ГРАФ ТАБЛИЦЕЙ СМЕЖНОСТИABCDEustr
20. Автор: Оркина Марина Александровна,преподаватель ГОУ СПО«Зубово-Полянский педагогический колледж»Республика Мордовия
21. Скачать презентанцию

ГРАФОМ G = (V, X) НАЗЫВАЕТСЯ ПАРА ДВУХ КОНЕЧНЫХ МНОЖЕСТВ: МНОЖЕСТВО ТОЧЕК И МНОЖЕСТВО ЛИНИЙ, СОЕДИНЯЮЩИХ НЕКОТОРЫЕ ПАРЫ ТОЧЕК. ВПЕРВЫЕ ПОНЯТИЕ «ГРАФ» ВВЕЛ В 1936

Слайды и текст этой презентации

Слайд 1ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
И ЕГО ЭЛЕМЕНТОВ
ГРАФА

Слайд 2 ГРАФОМ G = (V, X) НАЗЫВАЕТСЯ

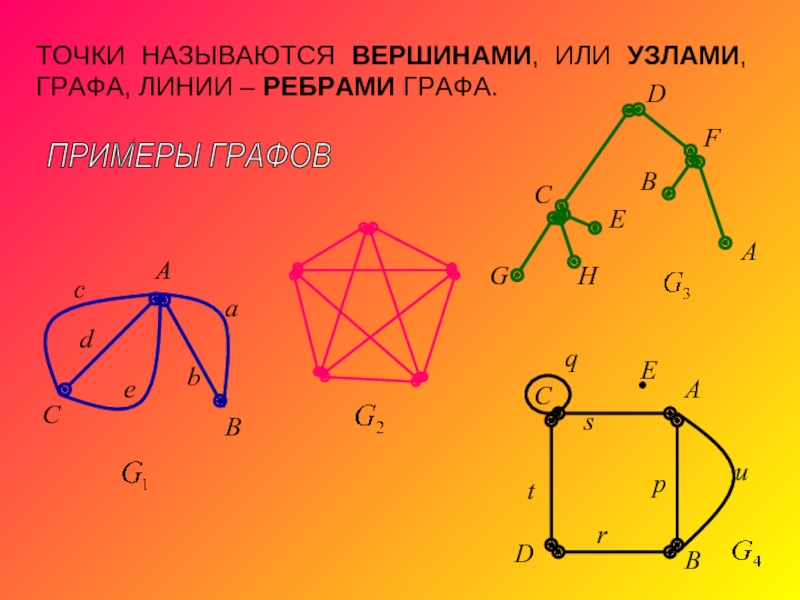
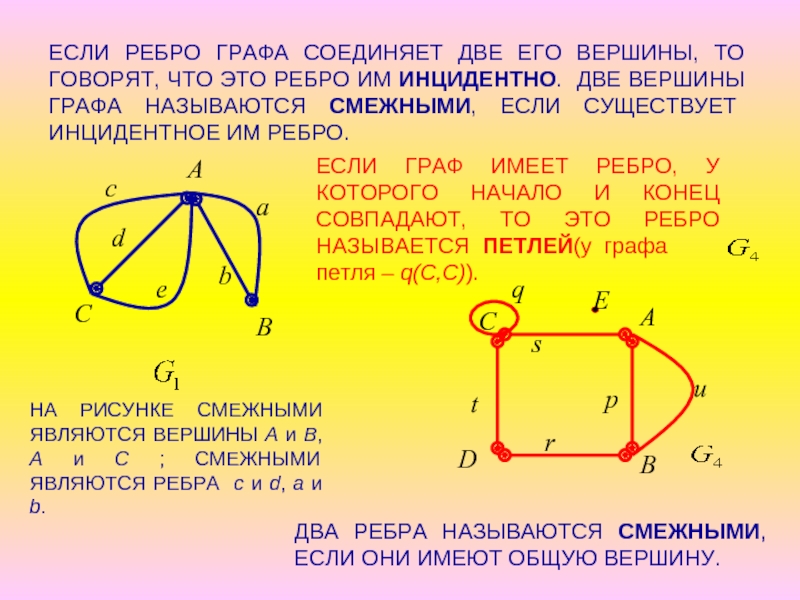
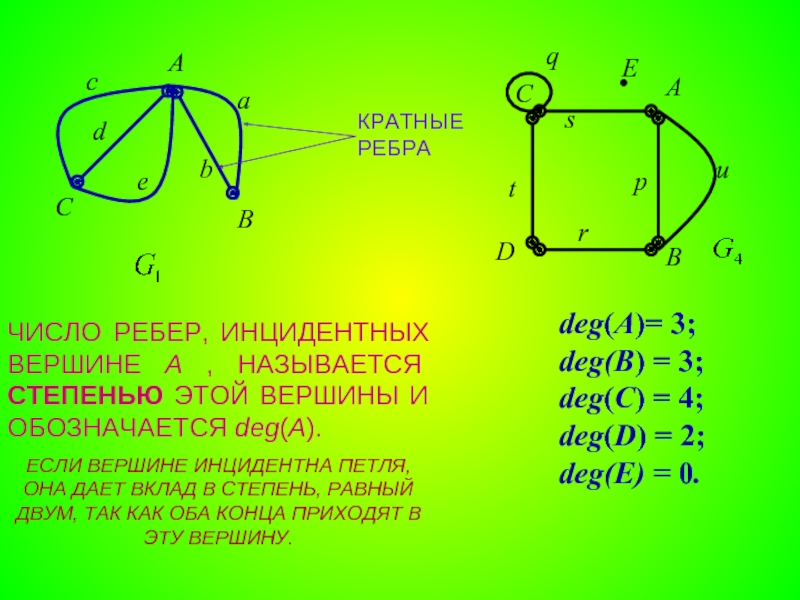
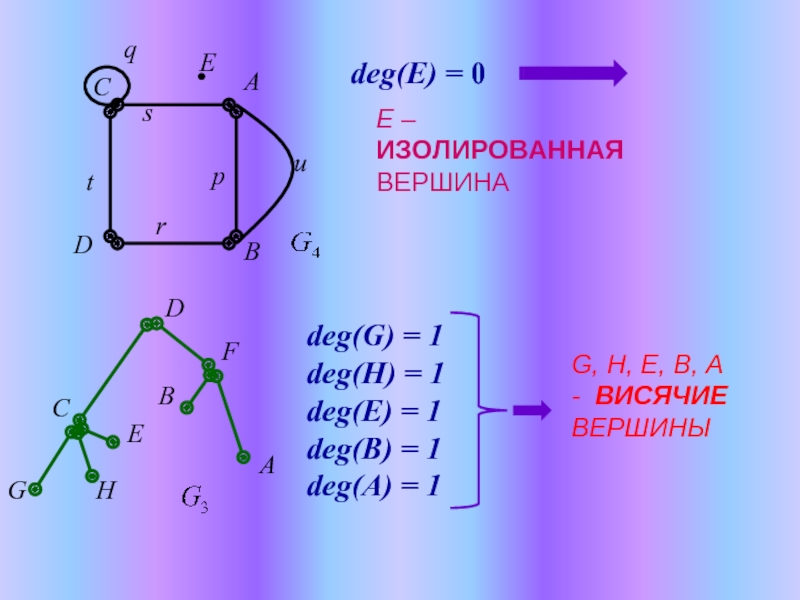
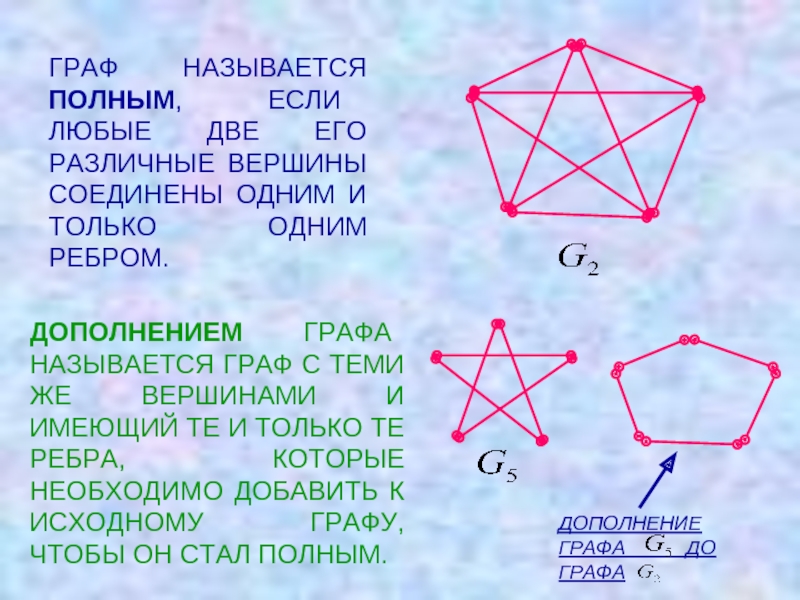
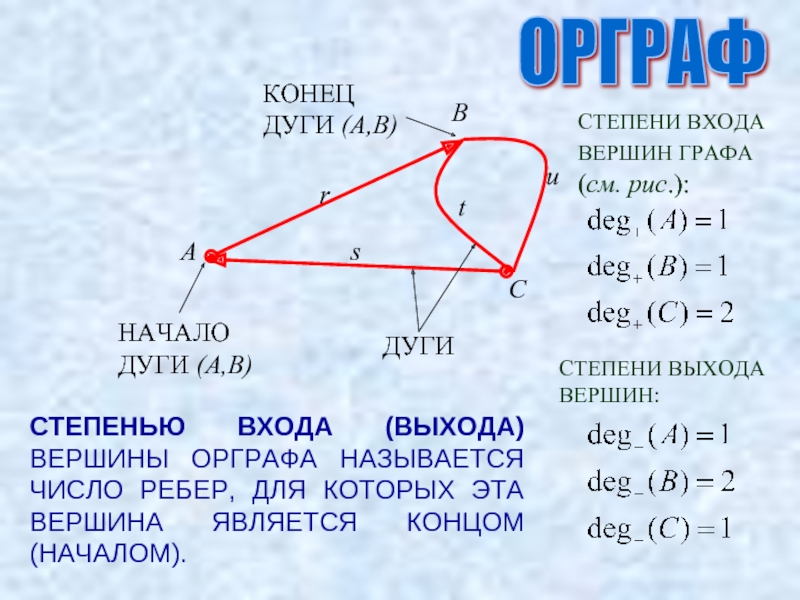
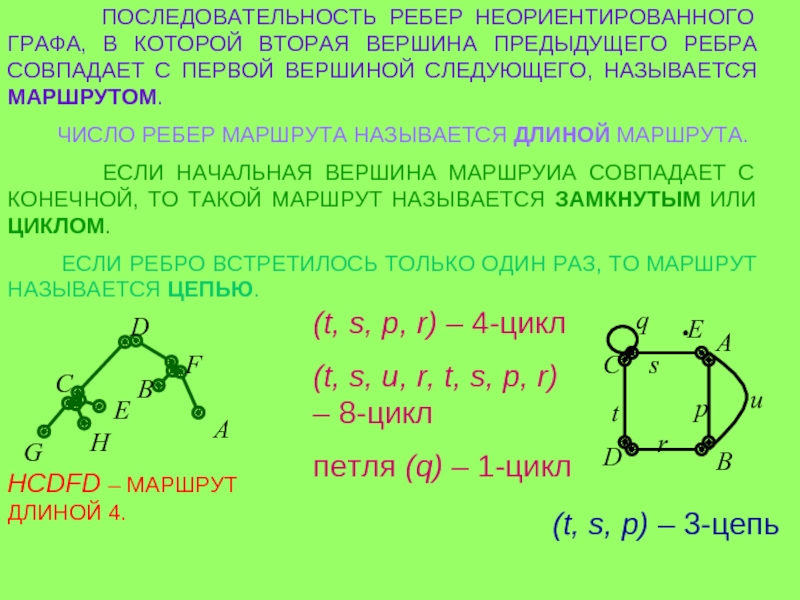
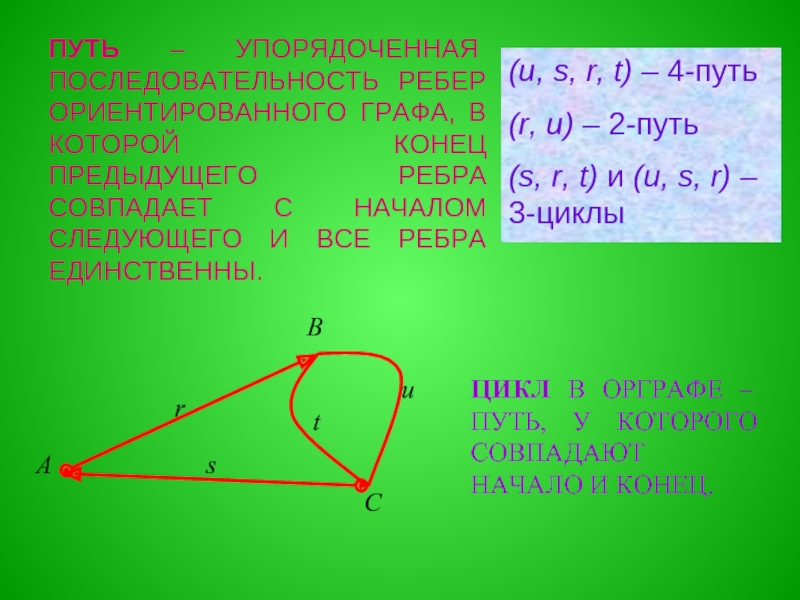
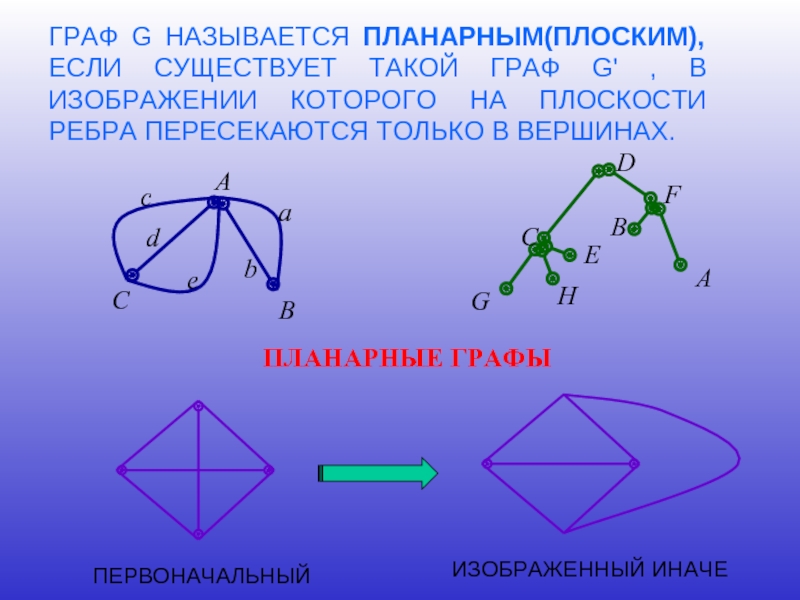
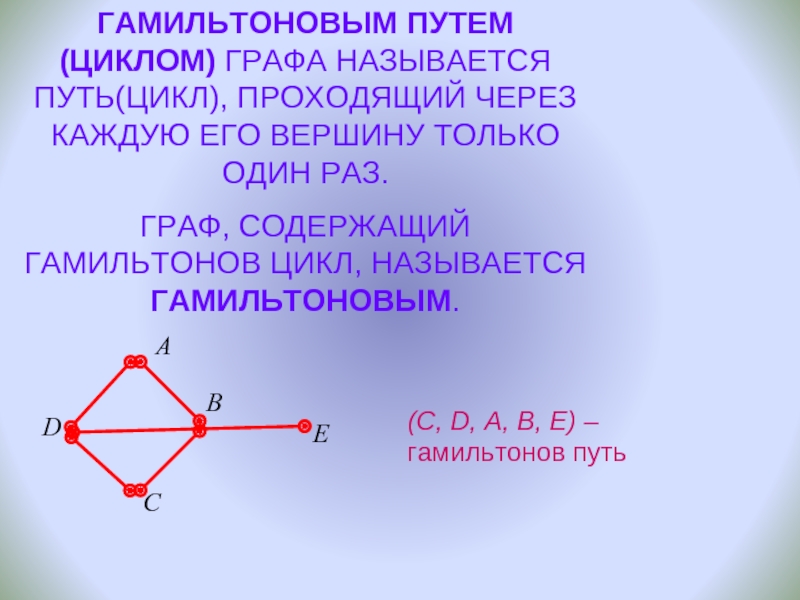
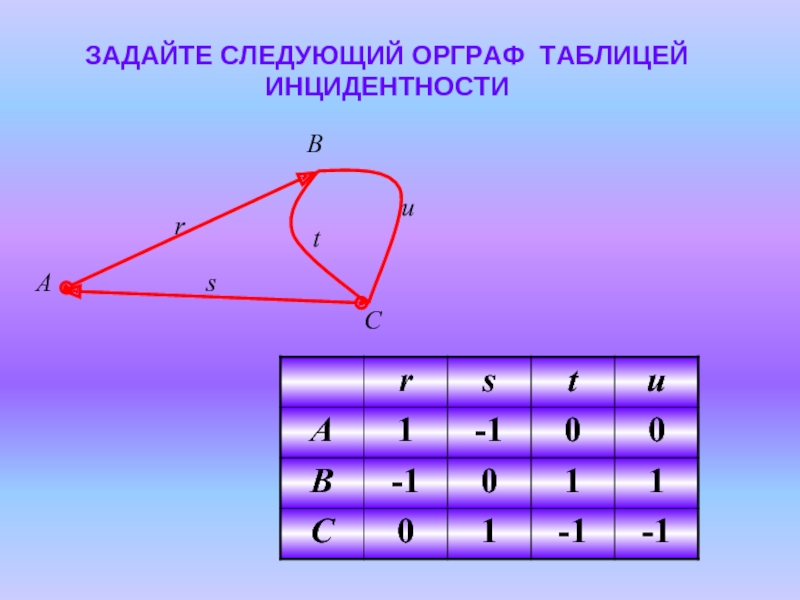
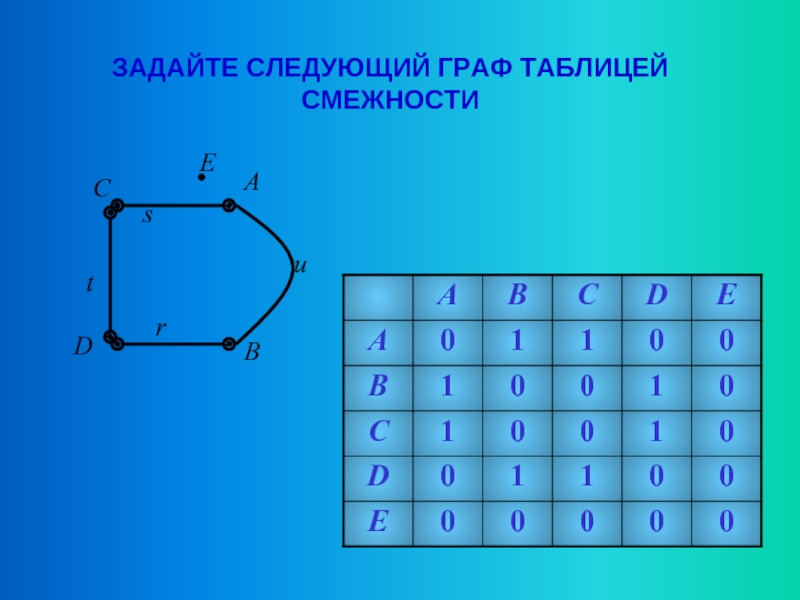
ПАРА ДВУХ КОНЕЧНЫХ МНОЖЕСТВ: МНОЖЕСТВО ТОЧЕК И МНОЖЕСТВО ЛИНИЙ, СОЕДИНЯЮЩИХ

НЕКОТОРЫЕ ПАРЫ ТОЧЕК.

ВПЕРВЫЕ ПОНЯТИЕ «ГРАФ» ВВЕЛ В 1936 г. ВЕНГЕРСКИЙ МАТЕМАТИК ДЕННИ КЁНИГ. НО ПЕРВАЯ РАБОТА ПО ТЕОРИИ ГРАФОВ ПРИНАДЛЕЖАЛА ПЕРУ ВЕЛИКОГО ЛЕОНАРДА ЭЙЛЕРА И БЫЛА НАПИСАНА ЕЩЕ В 1736 г.

ГРАФОМ G = (V, X) НАЗЫВАЕТСЯ ПАРА ДВУХ КОНЕЧНЫХ МНОЖЕСТВ: МНОЖЕСТВО ТОЧЕК И

Слайд 3ТОЧКИ НАЗЫВАЮТСЯ ВЕРШИНАМИ, ИЛИ УЗЛАМИ, ГРАФА, ЛИНИИ – РЕБРАМИ ГРАФА.
ПРИМЕРЫ

ГРАФОВ

Слайд 4ЕСЛИ РЕБРО ГРАФА СОЕДИНЯЕТ ДВЕ ЕГО ВЕРШИНЫ, ТО ГОВОРЯТ, ЧТО

ЭТО РЕБРО ИМ ИНЦИДЕНТНО. ДВЕ ВЕРШИНЫ ГРАФА НАЗЫВАЮТСЯ СМЕЖНЫМИ, ЕСЛИ

СУЩЕСТВУЕТ ИНЦИДЕНТНОЕ ИМ РЕБРО.

НА РИСУНКЕ СМЕЖНЫМИ ЯВЛЯЮТСЯ ВЕРШИНЫ A и B, A и C ; СМЕЖНЫМИ ЯВЛЯЮТСЯ РЕБРА c и d, a и b.

ЕСЛИ ГРАФ ИМЕЕТ РЕБРО, У КОТОРОГО НАЧАЛО И КОНЕЦ СОВПАДАЮТ, ТО ЭТО РЕБРО НАЗЫВАЕТСЯ ПЕТЛЕЙ(у графа петля – q(C,C)).

ДВА РЕБРА НАЗЫВАЮТСЯ СМЕЖНЫМИ, ЕСЛИ ОНИ ИМЕЮТ ОБЩУЮ ВЕРШИНУ.

ЕСЛИ РЕБРО ГРАФА СОЕДИНЯЕТ ДВЕ ЕГО ВЕРШИНЫ, ТО ГОВОРЯТ, ЧТО ЭТО РЕБРО ИМ ИНЦИДЕНТНО. ДВЕ ВЕРШИНЫ ГРАФА

Слайд 5КРАТНЫЕ РЕБРА
ЧИСЛО РЕБЕР, ИНЦИДЕНТНЫХ ВЕРШИНЕ A , НАЗЫВАЕТСЯ СТЕПЕНЬЮ ЭТОЙ

ВЕРШИНЫ И ОБОЗНАЧАЕТСЯ deg(A).
ЕСЛИ ВЕРШИНЕ ИНЦИДЕНТНА ПЕТЛЯ, ОНА ДАЕТ ВКЛАД

В СТЕПЕНЬ, РАВНЫЙ ДВУМ, ТАК КАК ОБА КОНЦА ПРИХОДЯТ В ЭТУ ВЕРШИНУ.

deg(A)= 3; deg(B) = 3; deg(C) = 4; deg(D) = 2; deg(E) = 0.

КРАТНЫЕ РЕБРАЧИСЛО РЕБЕР, ИНЦИДЕНТНЫХ ВЕРШИНЕ A , НАЗЫВАЕТСЯ СТЕПЕНЬЮ ЭТОЙ ВЕРШИНЫ И ОБОЗНАЧАЕТСЯ deg(A).ЕСЛИ ВЕРШИНЕ ИНЦИДЕНТНА ПЕТЛЯ,

Слайд 6deg(E) = 0

E – ИЗОЛИРОВАННАЯ ВЕРШИНА
deg(G) = 1
deg(H) = 1
deg(E)

= 1
deg(B) = 1
deg(A) = 1

G, H, E, B, A

- ВИСЯЧИЕ ВЕРШИНЫ

deg(E) = 0E – ИЗОЛИРОВАННАЯ ВЕРШИНАdeg(G) = 1deg(H) = 1deg(E) = 1deg(B) = 1deg(A) = 1G, H,

Слайд 7ТЕОРЕМА
В ГРАФЕ G(V, X) СУММА СТЕПЕНЕЙ ВСЕХ ЕГО ВЕРШИН –

ЧИСЛО ЧЕТНОЕ, РАВНОЕ УДВОЕННОМУ ЧИСЛУ РЕБЕР ГРАФА:
ВЕРШИНА НАЗЫВАЕТСЯ ЧЕТНОЙ

(НЕЧЕТНОЙ), ЕСЛИ ЕЕ СТЕПЕНЬ – ЧЕТНОЕ(НЕЧЕТНОЕ) ЧИСЛО.

ТЕОРЕМА

ЧИСЛО НЕЧЕТНЫХ ВЕРШИН ЛЮБОГО ГРАФА – ЧЕТНО.

СЛЕДСТВИЕ

НЕВОЗМОЖНО НАЧЕРТИТЬ ГРАФ С НЕЧЕТНЫМ ЧИСЛОМ НЕЧЕТНЫХ ВЕРШИН.

ТЕОРЕМАВ ГРАФЕ G(V, X) СУММА СТЕПЕНЕЙ ВСЕХ ЕГО ВЕРШИН – ЧИСЛО ЧЕТНОЕ, РАВНОЕ УДВОЕННОМУ ЧИСЛУ РЕБЕР ГРАФА:

Слайд 8ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО РАЗЛИЧНЫЕ ВЕРШИНЫ СОЕДИНЕНЫ

ОДНИМ И ТОЛЬКО ОДНИМ РЕБРОМ.
ДОПОЛНЕНИЕМ ГРАФА НАЗЫВАЕТСЯ ГРАФ С ТЕМИ

ЖЕ ВЕРШИНАМИ И ИМЕЮЩИЙ ТЕ И ТОЛЬКО ТЕ РЕБРА, КОТОРЫЕ НЕОБХОДИМО ДОБАВИТЬ К ИСХОДНОМУ ГРАФУ, ЧТОБЫ ОН СТАЛ ПОЛНЫМ.

ДОПОЛНЕНИЕ ГРАФА ДО ГРАФА

ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО РАЗЛИЧНЫЕ ВЕРШИНЫ СОЕДИНЕНЫ ОДНИМ И ТОЛЬКО ОДНИМ РЕБРОМ.ДОПОЛНЕНИЕМ ГРАФА НАЗЫВАЕТСЯ

Слайд 9ОРГРАФ
ДУГИ
НАЧАЛО ДУГИ (A,B)
КОНЕЦ ДУГИ (A,B)
СТЕПЕНЬЮ ВХОДА (ВЫХОДА) ВЕРШИНЫ ОРГРАФА НАЗЫВАЕТСЯ

ЧИСЛО РЕБЕР, ДЛЯ КОТОРЫХ ЭТА ВЕРШИНА ЯВЛЯЕТСЯ КОНЦОМ (НАЧАЛОМ).
СТЕПЕНИ ВХОДА

ВЕРШИН ГРАФА (см. рис.):

СТЕПЕНИ ВЫХОДА ВЕРШИН:

ОРГРАФДУГИНАЧАЛО ДУГИ (A,B)КОНЕЦ ДУГИ (A,B)СТЕПЕНЬЮ ВХОДА (ВЫХОДА) ВЕРШИНЫ ОРГРАФА НАЗЫВАЕТСЯ ЧИСЛО РЕБЕР, ДЛЯ КОТОРЫХ ЭТА ВЕРШИНА ЯВЛЯЕТСЯ

Слайд 10 ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР НЕОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ

ВТОРАЯ ВЕРШИНА ПРЕДЫДУЩЕГО РЕБРА СОВПАДАЕТ С ПЕРВОЙ ВЕРШИНОЙ СЛЕДУЮЩЕГО, НАЗЫВАЕТСЯ

МАРШРУТОМ.
ЧИСЛО РЕБЕР МАРШРУТА НАЗЫВАЕТСЯ ДЛИНОЙ МАРШРУТА.
ЕСЛИ НАЧАЛЬНАЯ ВЕРШИНА МАРШРУИА СОВПАДАЕТ С КОНЕЧНОЙ, ТО ТАКОЙ МАРШРУТ НАЗЫВАЕТСЯ ЗАМКНУТЫМ ИЛИ ЦИКЛОМ.
ЕСЛИ РЕБРО ВСТРЕТИЛОСЬ ТОЛЬКО ОДИН РАЗ, ТО МАРШРУТ НАЗЫВАЕТСЯ ЦЕПЬЮ.

HCDFD – МАРШРУТ ДЛИНОЙ 4.

(t, s, p, r) – 4-цикл
(t, s, u, r, t, s, p, r) – 8-цикл
петля (q) – 1-цикл

(t, s, p) – 3-цепь

ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР НЕОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ ВТОРАЯ ВЕРШИНА ПРЕДЫДУЩЕГО РЕБРА СОВПАДАЕТ С ПЕРВОЙ

Слайд 11ПУТЬ – УПОРЯДОЧЕННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР ОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ КОНЕЦ

ПРЕДЫДУЩЕГО РЕБРА СОВПАДАЕТ С НАЧАЛОМ СЛЕДУЮЩЕГО И ВСЕ РЕБРА ЕДИНСТВЕННЫ.
ЦИКЛ

В ОРГРАФЕ – ПУТЬ, У КОТОРОГО СОВПАДАЮТ НАЧАЛО И КОНЕЦ.

(u, s, r, t) – 4-путь
(r, u) – 2-путь
(s, r, t) и (u, s, r) – 3-циклы

ПУТЬ – УПОРЯДОЧЕННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР ОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ КОНЕЦ ПРЕДЫДУЩЕГО РЕБРА СОВПАДАЕТ С НАЧАЛОМ СЛЕДУЮЩЕГО И

Слайд 12ЦЕПЬ, ПУТЬ И ЦИКЛ В ГРАФЕ НАЗЫВАЮТСЯ ПРОСТЫМИ, ЕСЛИ ОНИ

ПРОХОДЯТ ЧЕРЕЗ ЛЮБУЮ ИЗ ВЕРШИН НЕ БОЛЕЕ ОДНОГО РАЗА.
НЕОРИЕНТИРОВАННЫЙ ГРАФ

НАЗЫВАЕТСЯ СВЯЗНЫМ, ЕСЛИ МЕЖДУ ЛЮБЫМИ ДВУМЯ ЕГО ВЕРШИНАМИ ЕСТЬ МАРШРУТ.

ТЕОРЕМА

ДЛЯ ТОГО, ЧТОБЫ СВЯЗНЫЙ ГРАФ ЯВЛЯЛСЯ ПРОСТЫМ ЦИКЛОМ, НЕОБХОДИМО И ДОСТАТОЧНО, ЧТОБЫ КАЖДАЯ ЕГО ВЕРШИНА ИМЕЛА СТЕПЕНЬ, РАВНУЮ 2.

ЦЕПЬ, ПУТЬ И ЦИКЛ В ГРАФЕ НАЗЫВАЮТСЯ ПРОСТЫМИ, ЕСЛИ ОНИ ПРОХОДЯТ ЧЕРЕЗ ЛЮБУЮ ИЗ ВЕРШИН НЕ БОЛЕЕ

Слайд 13ГРАФ G НАЗЫВАЕТСЯ ПЛАНАРНЫМ(ПЛОСКИМ), ЕСЛИ СУЩЕСТВУЕТ ТАКОЙ ГРАФ G' ,

В ИЗОБРАЖЕНИИ КОТОРОГО НА ПЛОСКОСТИ РЕБРА ПЕРЕСЕКАЮТСЯ ТОЛЬКО В ВЕРШИНАХ.
C
A
B
a
b
c
d
e
G
H
E
C
D
F
A
B
ПЛАНАРНЫЕ

ГРАФЫ

ПЕРВОНАЧАЛЬНЫЙ

ИЗОБРАЖЕННЫЙ ИНАЧЕ

ГРАФ G НАЗЫВАЕТСЯ ПЛАНАРНЫМ(ПЛОСКИМ), ЕСЛИ СУЩЕСТВУЕТ ТАКОЙ ГРАФ G' , В ИЗОБРАЖЕНИИ КОТОРОГО НА ПЛОСКОСТИ РЕБРА ПЕРЕСЕКАЮТСЯ

Слайд 14ЭЙЛЕРОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), КОТОРЫЙ СОДЕРЖИТ ВСЕ РЕБРА ГРАФА

ТОЛЬКО ОДИН РАЗ.
ГРАФ, ОБЛАДАЮЩИЙ ЭЙЛЕРОВЫМ ЦИКЛОМ, НАЗЫВАЕТСЯ ЭЙЛЕРОВЫМ.
ТЕОРЕМА
ГРАФ ЯВЛЯЕТСЯ ЭЙЛЕРОВЫМ

ТОГДА И ТОЛЬКО ТОГДА, КОГДА ОН – СВЯЗНЫЙ ГРАФ, ИМЕЮЩИЙ ВСЕ ЧЕТНЫЕ ВЕРШИНЫ.

ЭЙЛЕРОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), КОТОРЫЙ СОДЕРЖИТ ВСЕ РЕБРА ГРАФА ТОЛЬКО ОДИН РАЗ.ГРАФ, ОБЛАДАЮЩИЙ ЭЙЛЕРОВЫМ ЦИКЛОМ, НАЗЫВАЕТСЯ

Слайд 15ГАМИЛЬТОНОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), ПРОХОДЯЩИЙ ЧЕРЕЗ КАЖДУЮ ЕГО ВЕРШИНУ

ТОЛЬКО ОДИН РАЗ.
ГРАФ, СОДЕРЖАЩИЙ ГАМИЛЬТОНОВ ЦИКЛ, НАЗЫВАЕТСЯ ГАМИЛЬТОНОВЫМ.
A
B
C
D
E
(C, D, A,

B, E) – гамильтонов путь

ГАМИЛЬТОНОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), ПРОХОДЯЩИЙ ЧЕРЕЗ КАЖДУЮ ЕГО ВЕРШИНУ ТОЛЬКО ОДИН РАЗ.ГРАФ, СОДЕРЖАЩИЙ ГАМИЛЬТОНОВ ЦИКЛ, НАЗЫВАЕТСЯ

Слайд 16МАТРИЦЕЙ ИНЦИДЕНТНОСТИ ГРАФА G НАЗЫВАЮТ ТАБЛИЦУ B, СОСТОЯЩУЮ ИЗ n

СТРОК(ВЕРШИНЫ) И m СТОЛБЦОВ(РЕБРА), В КОТОРОЙ:
ДЛЯ НЕОРИЕНТИРОВАННОГО ГРАФА:
, ЕСЛИ ВЕРШИНА

ИНЦИДЕНТНА РЕБРУ

, ЕСЛИ ВЕРШИНА

ИНЦИДЕНТНА РЕБРУ

ДЛЯ ОРИЕНТИРОВАННОГО ГРАФА:

, ЕСЛИ ВЕРШИНА

ЯВЛЯЕТСЯ НАЧАЛОМ ДУГИ

, ЕСЛИ ВЕРШИНА

НЕ ИНЦИДЕНТНА ДУГЕ

, ЕСЛИ ВЕРШИНА

ЯВЛЯЕТСЯ КОНЦОМ ДУГИ

МАТРИЦЕЙ ИНЦИДЕНТНОСТИ ГРАФА G НАЗЫВАЮТ ТАБЛИЦУ B, СОСТОЯЩУЮ ИЗ n СТРОК(ВЕРШИНЫ) И m СТОЛБЦОВ(РЕБРА), В КОТОРОЙ:ДЛЯ НЕОРИЕНТИРОВАННОГО

Слайд 17МАТРИЦЕЙ СМЕЖНОСТИ ГРАФА G(V,X) БЕЗ КРАТНЫХ РЕБЕР НАЗЫВАЮТ КВАДРАТНУЮ МАТРИЦУ

A ПОРЯДКА n, В КОТОРОЙ:
, ЕСЛИ
, ЕСЛИ

МАТРИЦЕЙ СМЕЖНОСТИ ГРАФА G(V,X) БЕЗ КРАТНЫХ РЕБЕР НАЗЫВАЮТ КВАДРАТНУЮ МАТРИЦУ A ПОРЯДКА n, В КОТОРОЙ:, ЕСЛИ ,

Слайд 18ЗАДАЙТЕ СЛЕДУЮЩИЙ ОРГРАФ ТАБЛИЦЕЙ ИНЦИДЕНТНОСТИ

Слайд 19ЗАДАЙТЕ СЛЕДУЮЩИЙ ГРАФ ТАБЛИЦЕЙ СМЕЖНОСТИ

A
B
C
D
E
u
s
t
r

Слайд 20Автор: Оркина Марина Александровна,
преподаватель ГОУ СПО
«Зубово-Полянский педагогический колледж»
Республика Мордовия

Скачать презентацию

Теги

Разделы презентаций

Графа и его элементы

Содержание

Слайды и текст этой презентации

Слайд 1ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯИ ЕГО ЭЛЕМЕНТОВГРАФА

Слайд 2 ГРАФОМ G = (V, X) НАЗЫВАЕТСЯ

ПАРА ДВУХ КОНЕЧНЫХ МНОЖЕСТВ: МНОЖЕСТВО ТОЧЕК И МНОЖЕСТВО ЛИНИЙ, СОЕДИНЯЮЩИХ

Слайд 3ТОЧКИ НАЗЫВАЮТСЯ ВЕРШИНАМИ, ИЛИ УЗЛАМИ, ГРАФА, ЛИНИИ – РЕБРАМИ ГРАФА.ПРИМЕРЫ

ГРАФОВ

Слайд 4ЕСЛИ РЕБРО ГРАФА СОЕДИНЯЕТ ДВЕ ЕГО ВЕРШИНЫ, ТО ГОВОРЯТ, ЧТО

ЭТО РЕБРО ИМ ИНЦИДЕНТНО. ДВЕ ВЕРШИНЫ ГРАФА НАЗЫВАЮТСЯ СМЕЖНЫМИ, ЕСЛИ

Слайд 5КРАТНЫЕ РЕБРАЧИСЛО РЕБЕР, ИНЦИДЕНТНЫХ ВЕРШИНЕ A , НАЗЫВАЕТСЯ СТЕПЕНЬЮ ЭТОЙ

ВЕРШИНЫ И ОБОЗНАЧАЕТСЯ deg(A).ЕСЛИ ВЕРШИНЕ ИНЦИДЕНТНА ПЕТЛЯ, ОНА ДАЕТ ВКЛАД

Слайд 6deg(E) = 0E – ИЗОЛИРОВАННАЯ ВЕРШИНАdeg(G) = 1deg(H) = 1deg(E)

= 1deg(B) = 1deg(A) = 1G, H, E, B, A

Слайд 7ТЕОРЕМАВ ГРАФЕ G(V, X) СУММА СТЕПЕНЕЙ ВСЕХ ЕГО ВЕРШИН –

ЧИСЛО ЧЕТНОЕ, РАВНОЕ УДВОЕННОМУ ЧИСЛУ РЕБЕР ГРАФА: ВЕРШИНА НАЗЫВАЕТСЯ ЧЕТНОЙ

Слайд 8ГРАФ НАЗЫВАЕТСЯ ПОЛНЫМ, ЕСЛИ ЛЮБЫЕ ДВЕ ЕГО РАЗЛИЧНЫЕ ВЕРШИНЫ СОЕДИНЕНЫ

ОДНИМ И ТОЛЬКО ОДНИМ РЕБРОМ.ДОПОЛНЕНИЕМ ГРАФА НАЗЫВАЕТСЯ ГРАФ С ТЕМИ

Слайд 9ОРГРАФДУГИНАЧАЛО ДУГИ (A,B)КОНЕЦ ДУГИ (A,B)СТЕПЕНЬЮ ВХОДА (ВЫХОДА) ВЕРШИНЫ ОРГРАФА НАЗЫВАЕТСЯ

ЧИСЛО РЕБЕР, ДЛЯ КОТОРЫХ ЭТА ВЕРШИНА ЯВЛЯЕТСЯ КОНЦОМ (НАЧАЛОМ).СТЕПЕНИ ВХОДА

Слайд 10 ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР НЕОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ

ВТОРАЯ ВЕРШИНА ПРЕДЫДУЩЕГО РЕБРА СОВПАДАЕТ С ПЕРВОЙ ВЕРШИНОЙ СЛЕДУЮЩЕГО, НАЗЫВАЕТСЯ

Слайд 11ПУТЬ – УПОРЯДОЧЕННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ РЕБЕР ОРИЕНТИРОВАННОГО ГРАФА, В КОТОРОЙ КОНЕЦ

ПРЕДЫДУЩЕГО РЕБРА СОВПАДАЕТ С НАЧАЛОМ СЛЕДУЮЩЕГО И ВСЕ РЕБРА ЕДИНСТВЕННЫ.ЦИКЛ

Слайд 12ЦЕПЬ, ПУТЬ И ЦИКЛ В ГРАФЕ НАЗЫВАЮТСЯ ПРОСТЫМИ, ЕСЛИ ОНИ

ПРОХОДЯТ ЧЕРЕЗ ЛЮБУЮ ИЗ ВЕРШИН НЕ БОЛЕЕ ОДНОГО РАЗА.НЕОРИЕНТИРОВАННЫЙ ГРАФ

Слайд 13ГРАФ G НАЗЫВАЕТСЯ ПЛАНАРНЫМ(ПЛОСКИМ), ЕСЛИ СУЩЕСТВУЕТ ТАКОЙ ГРАФ G' ,

В ИЗОБРАЖЕНИИ КОТОРОГО НА ПЛОСКОСТИ РЕБРА ПЕРЕСЕКАЮТСЯ ТОЛЬКО В ВЕРШИНАХ.CABabcdeGHECDFABПЛАНАРНЫЕ

Слайд 14ЭЙЛЕРОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), КОТОРЫЙ СОДЕРЖИТ ВСЕ РЕБРА ГРАФА

ТОЛЬКО ОДИН РАЗ.ГРАФ, ОБЛАДАЮЩИЙ ЭЙЛЕРОВЫМ ЦИКЛОМ, НАЗЫВАЕТСЯ ЭЙЛЕРОВЫМ.ТЕОРЕМАГРАФ ЯВЛЯЕТСЯ ЭЙЛЕРОВЫМ

Слайд 15ГАМИЛЬТОНОВЫМ ПУТЕМ(ЦИКЛОМ) ГРАФА НАЗЫВАЕТСЯ ПУТЬ(ЦИКЛ), ПРОХОДЯЩИЙ ЧЕРЕЗ КАЖДУЮ ЕГО ВЕРШИНУ

ТОЛЬКО ОДИН РАЗ.ГРАФ, СОДЕРЖАЩИЙ ГАМИЛЬТОНОВ ЦИКЛ, НАЗЫВАЕТСЯ ГАМИЛЬТОНОВЫМ.ABCDE(C, D, A,

Слайд 16МАТРИЦЕЙ ИНЦИДЕНТНОСТИ ГРАФА G НАЗЫВАЮТ ТАБЛИЦУ B, СОСТОЯЩУЮ ИЗ n

СТРОК(ВЕРШИНЫ) И m СТОЛБЦОВ(РЕБРА), В КОТОРОЙ:ДЛЯ НЕОРИЕНТИРОВАННОГО ГРАФА:, ЕСЛИ ВЕРШИНА

Слайд 17МАТРИЦЕЙ СМЕЖНОСТИ ГРАФА G(V,X) БЕЗ КРАТНЫХ РЕБЕР НАЗЫВАЮТ КВАДРАТНУЮ МАТРИЦУ

A ПОРЯДКА n, В КОТОРОЙ:, ЕСЛИ , ЕСЛИ

Слайд 18ЗАДАЙТЕ СЛЕДУЮЩИЙ ОРГРАФ ТАБЛИЦЕЙ ИНЦИДЕНТНОСТИ

Слайд 19ЗАДАЙТЕ СЛЕДУЮЩИЙ ГРАФ ТАБЛИЦЕЙ СМЕЖНОСТИABCDEustr

Слайд 20Автор: Оркина Марина Александровна,преподаватель ГОУ СПО«Зубово-Полянский педагогический колледж»Республика Мордовия

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
И ЕГО ЭЛЕМЕНТОВ
ГРАФА

Слайд 3ТОЧКИ НАЗЫВАЮТСЯ ВЕРШИНАМИ, ИЛИ УЗЛАМИ, ГРАФА, ЛИНИИ – РЕБРАМИ ГРАФА.
ПРИМЕРЫ

Слайд 5КРАТНЫЕ РЕБРА
ЧИСЛО РЕБЕР, ИНЦИДЕНТНЫХ ВЕРШИНЕ A , НАЗЫВАЕТСЯ СТЕПЕНЬЮ ЭТОЙ

ВЕРШИНЫ И ОБОЗНАЧАЕТСЯ deg(A).
ЕСЛИ ВЕРШИНЕ ИНЦИДЕНТНА ПЕТЛЯ, ОНА ДАЕТ ВКЛАД

Слайд 6deg(E) = 0

E – ИЗОЛИРОВАННАЯ ВЕРШИНА
deg(G) = 1
deg(H) = 1
deg(E)

= 1
deg(B) = 1
deg(A) = 1

G, H, E, B, A

Слайд 7ТЕОРЕМА
В ГРАФЕ G(V, X) СУММА СТЕПЕНЕЙ ВСЕХ ЕГО ВЕРШИН –

ЧИСЛО ЧЕТНОЕ, РАВНОЕ УДВОЕННОМУ ЧИСЛУ РЕБЕР ГРАФА:
ВЕРШИНА НАЗЫВАЕТСЯ ЧЕТНОЙ

ОДНИМ И ТОЛЬКО ОДНИМ РЕБРОМ.
ДОПОЛНЕНИЕМ ГРАФА НАЗЫВАЕТСЯ ГРАФ С ТЕМИ

Слайд 9ОРГРАФ
ДУГИ
НАЧАЛО ДУГИ (A,B)
КОНЕЦ ДУГИ (A,B)
СТЕПЕНЬЮ ВХОДА (ВЫХОДА) ВЕРШИНЫ ОРГРАФА НАЗЫВАЕТСЯ

ЧИСЛО РЕБЕР, ДЛЯ КОТОРЫХ ЭТА ВЕРШИНА ЯВЛЯЕТСЯ КОНЦОМ (НАЧАЛОМ).
СТЕПЕНИ ВХОДА

ПРЕДЫДУЩЕГО РЕБРА СОВПАДАЕТ С НАЧАЛОМ СЛЕДУЮЩЕГО И ВСЕ РЕБРА ЕДИНСТВЕННЫ.
ЦИКЛ

ПРОХОДЯТ ЧЕРЕЗ ЛЮБУЮ ИЗ ВЕРШИН НЕ БОЛЕЕ ОДНОГО РАЗА.
НЕОРИЕНТИРОВАННЫЙ ГРАФ

В ИЗОБРАЖЕНИИ КОТОРОГО НА ПЛОСКОСТИ РЕБРА ПЕРЕСЕКАЮТСЯ ТОЛЬКО В ВЕРШИНАХ.
C
A
B
a
b
c
d
e
G
H
E
C
D
F
A
B
ПЛАНАРНЫЕ

ТОЛЬКО ОДИН РАЗ.
ГРАФ, ОБЛАДАЮЩИЙ ЭЙЛЕРОВЫМ ЦИКЛОМ, НАЗЫВАЕТСЯ ЭЙЛЕРОВЫМ.
ТЕОРЕМА
ГРАФ ЯВЛЯЕТСЯ ЭЙЛЕРОВЫМ

ТОЛЬКО ОДИН РАЗ.
ГРАФ, СОДЕРЖАЩИЙ ГАМИЛЬТОНОВ ЦИКЛ, НАЗЫВАЕТСЯ ГАМИЛЬТОНОВЫМ.
A
B
C
D
E
(C, D, A,

СТРОК(ВЕРШИНЫ) И m СТОЛБЦОВ(РЕБРА), В КОТОРОЙ:
ДЛЯ НЕОРИЕНТИРОВАННОГО ГРАФА:
, ЕСЛИ ВЕРШИНА

A ПОРЯДКА n, В КОТОРОЙ:
, ЕСЛИ
, ЕСЛИ

Слайд 19ЗАДАЙТЕ СЛЕДУЮЩИЙ ГРАФ ТАБЛИЦЕЙ СМЕЖНОСТИ

A
B
C
D
E
u
s
t
r

Слайд 20Автор: Оркина Марина Александровна,
преподаватель ГОУ СПО
«Зубово-Полянский педагогический колледж»
Республика Мордовия