Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Графический метод решения уравнений с параметром
Содержание
- 1. Графический метод решения уравнений с параметром
- 2. Скільки розв'язків має рівняння в залежності від значення параметра а ?
- 3. Розв'язуванняПозначимо:
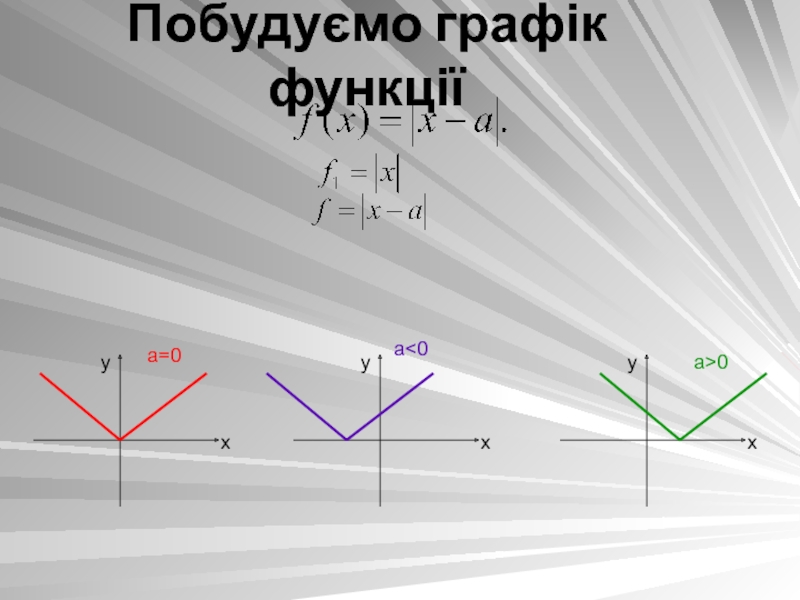
- 4. Побудуємо графік функції
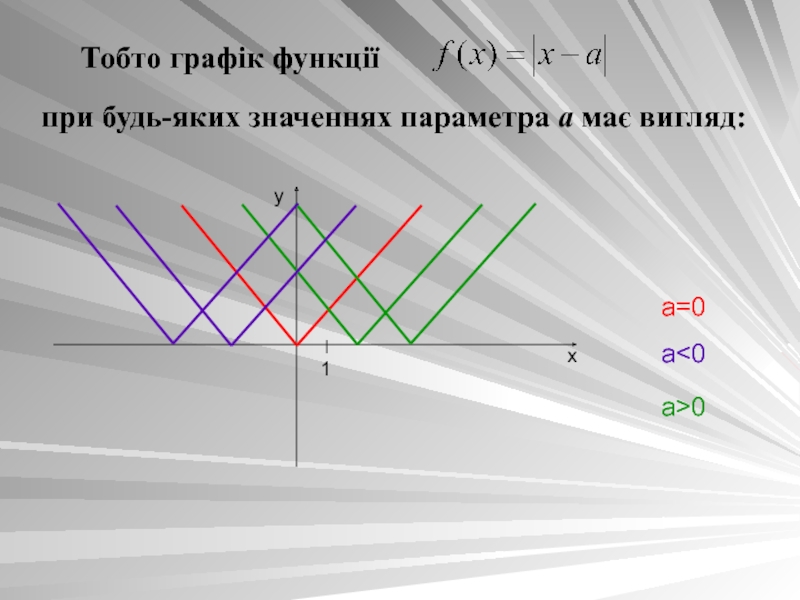
- 5. Тобто графік функціїпри будь-яких значеннях параметра а має вигляд:
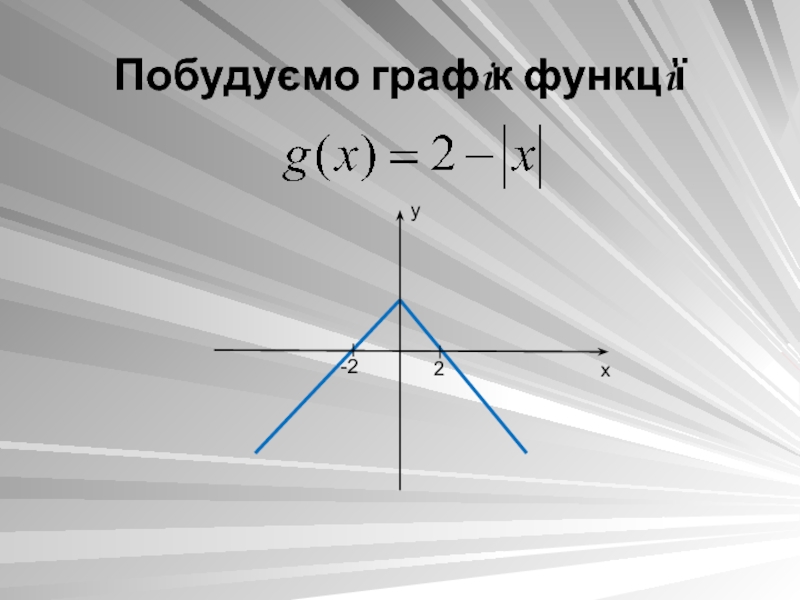
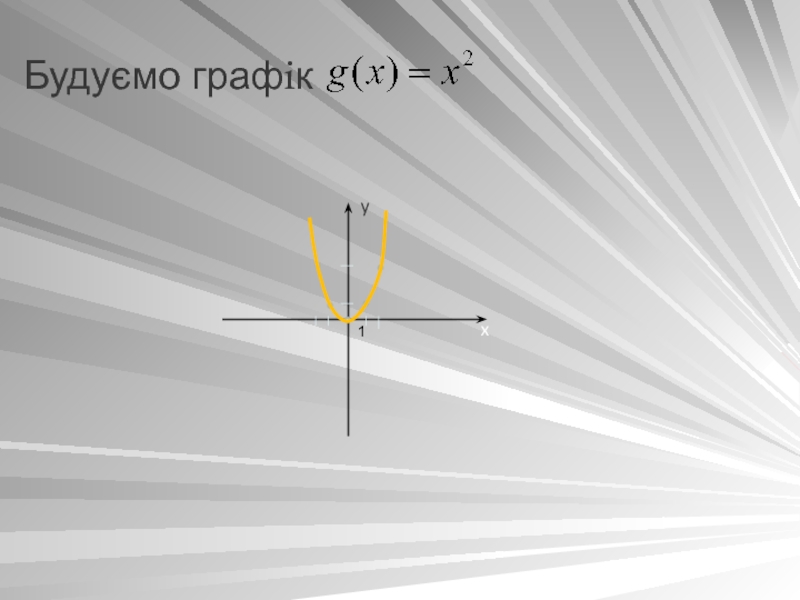
- 6. Побудуємо графiк функцiї
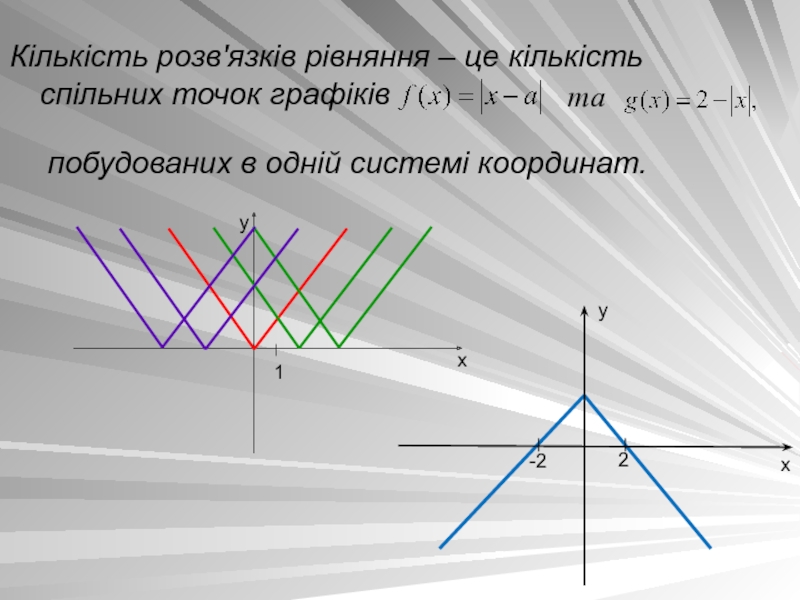
- 7. Кількість розв'язків рівняння – це кількість спільних точок графіків тапобудованих в одній системі координат.
- 8. Слайд 8
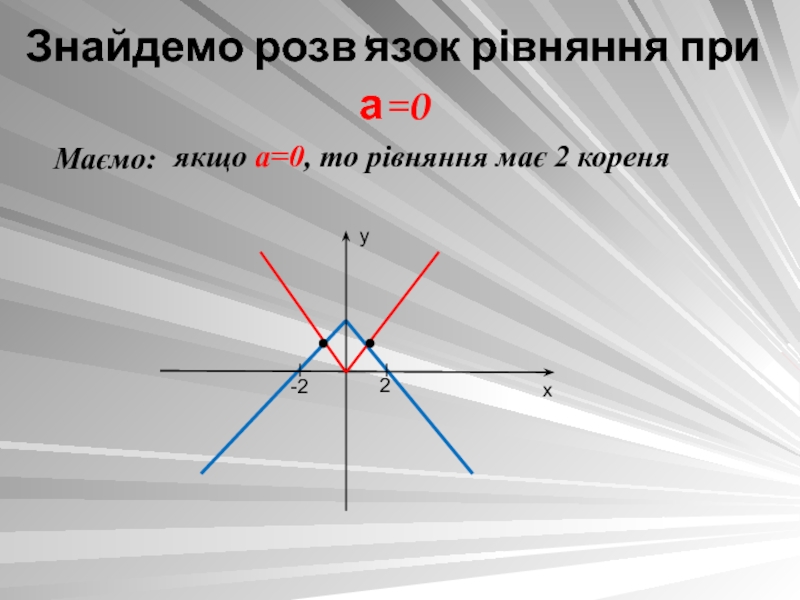
- 9. Знайдемо розв'язок рівняння при а=0 Маємо:якщо а=0, то рівняння має 2 кореня
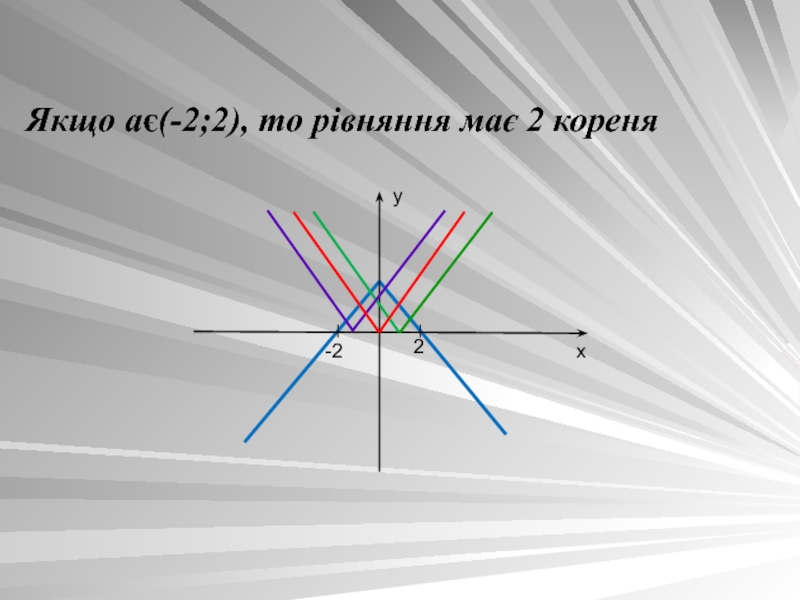
- 10. Якщо ає(-2;2), то рівняння має 2 кореня
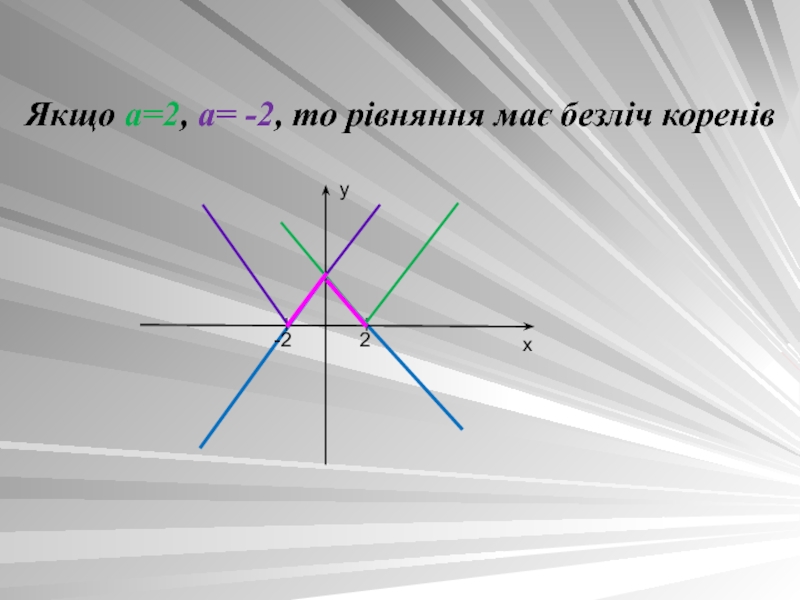
- 11. Якщо а=2, а= -2, то рівняння має безліч коренiв
- 12. Якщо а2, то рівняння не має розв'язків
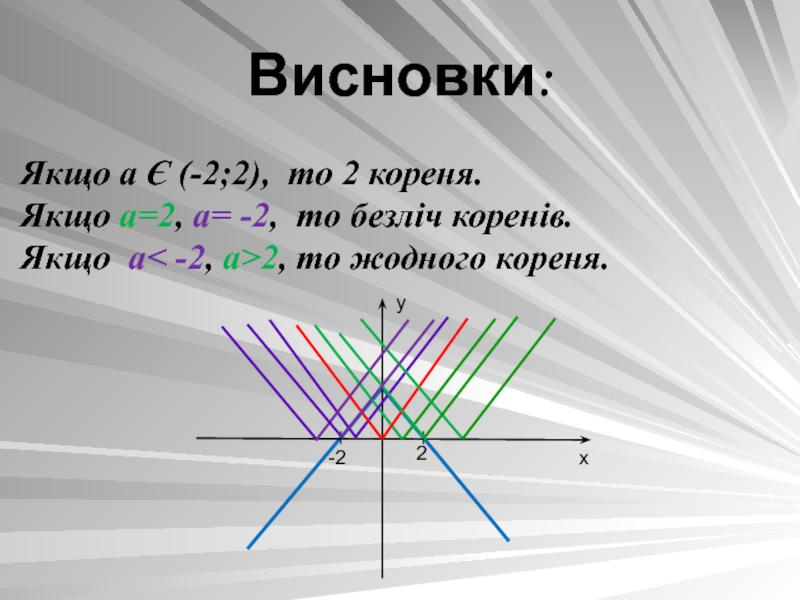
- 13. Висновки:Якщо а Є (-2;2), то 2 кореня.Якщо
- 14. Вiдповiдь:при аЄ (-2;2) 2 кореня,при а=2, а=-2 безліч коренів,при а>2, а
- 15. в залежності від значення параметра а ?Скільки розв'язків має рівняння
- 16. Розв’язанняНехай Тобто, треба визначити: скiльки точок перетину можуть мати графiки цих функцiй.
- 17. Будуємо графiк функції уууха=0
- 18. Маємо:a>0a=0a
- 19. Будуємо графiк1
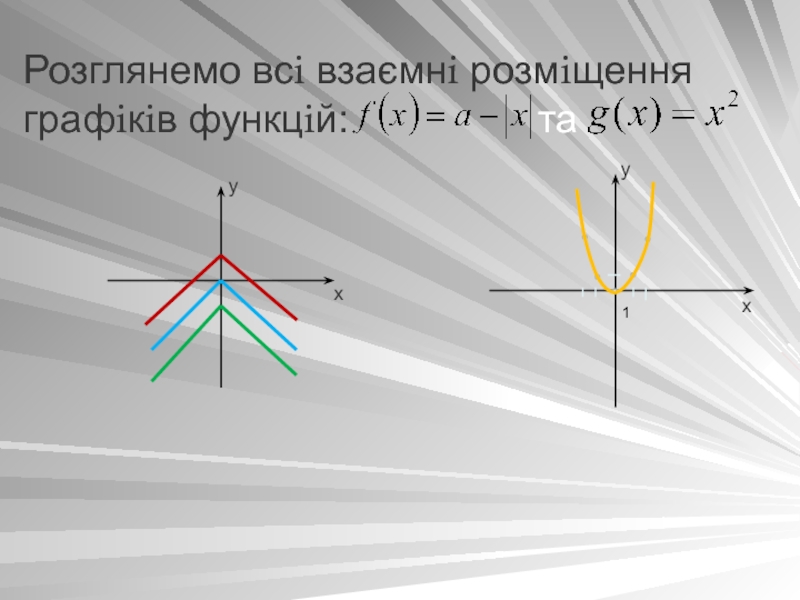
- 20. Розглянемо всi взаємнi розмiщення графiкiв функцiй: та х
- 21. 1 випадок: якщо , то 1 корiньyа=0
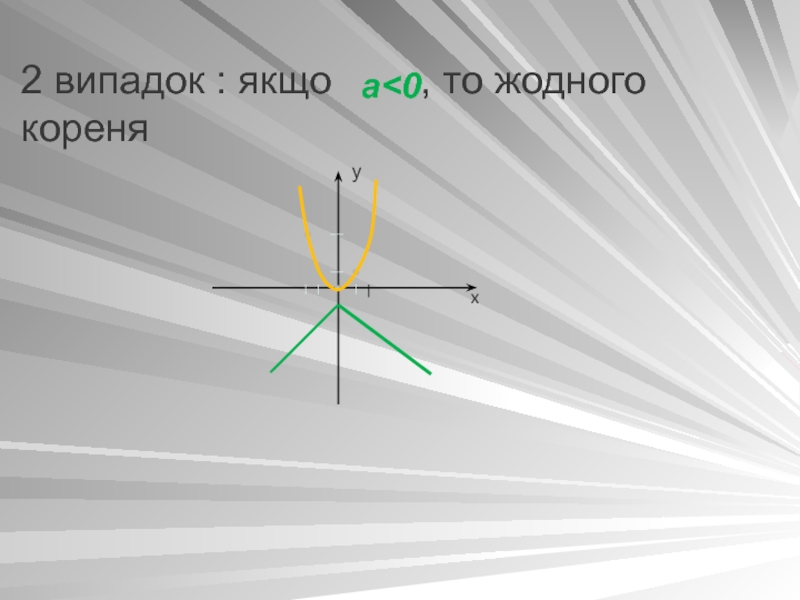
- 22. 2 випадок : якщо , то жодного кореняа
- 23. 3 випадок: якщо , то 2 кореняа>0у
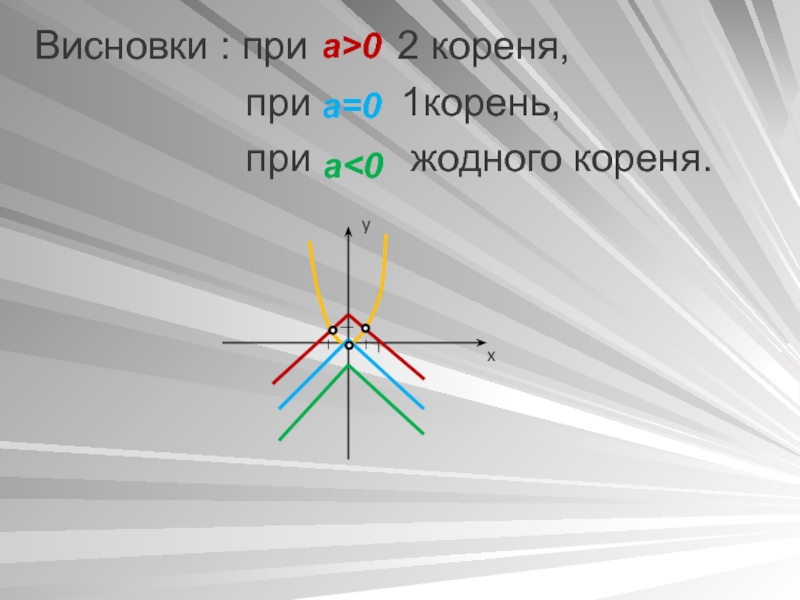
- 24. Висновки : при
- 25. Отже маємо таку вiповiдь:при
- 26. Скачать презентанцию
Скільки розв'язків має рівняння в залежності від значення параметра а ?
Слайды и текст этой презентации
Слайд 1Графічний метод розв’язування рівнянь з параметром
Проект виконала
Учениця 10 класу
Кім Діана
Керівник
проекту
Слайд 7Кількість розв'язків рівняння – це кількість спільних точок графіків
та
побудованих
в одній системі координат.
Слайд 13Висновки:
Якщо а Є (-2;2), то 2 кореня.
Якщо а=2, а= -2,
то безліч коренів.
Якщо а< -2, а>2, то жодного кореня.
Слайд 16Розв’язання
Нехай
Тобто, треба визначити: скiльки точок перетину можуть мати графiки
цих функцiй.
Слайд 18Маємо:
a>0
a=0
a
,будуємо графік вiдомоÏ елементарноÏ
функцiÏ ,який вiдображаємо симетрично вiсi х та перемiщуєму вздовж вiсi у в залежностівiд значення параметру а.